A Visual Guide to Evolution Strategies
本文是对 David Ha(hardmaru)博客 A Visual Guide to Evolution Strategies 的阅读笔记。该笔记写于2017年10月29日。
原文:https://blog.otoro.net/2017/10/29/visual-evolution-strategies/
1. 引言
深度学习之所以强,核心在于反向传播(Backpropagation)能高效计算目标函数关于参数的梯度,从而在高维参数空间里快速优化。
但有一些问题里反向传播不好用或根本用不了,典型例子是强化学习(RL):
- 信用分配难:现在的动作如何“归因”到未来若干步后的奖励?尤其是当奖励延迟很久才出现时。
- 奖励稀疏 + 噪声大:真实世界常常只在很久以后给一次总体奖励。作者用“年终奖金”打比方:你可能年底才拿到一笔奖金,但很难确切知道这一年里哪一个具体行为导致了奖金的高低。这种情况下,对未来回报的梯度估计会非常嘈杂,甚至“看起来像是随机的”。
- 局部最优(Local Optima):即便能算梯度,RL 任务的目标函数往往极其复杂、非凸,很容易卡在局部最优。
 Stuck in a local optimum.
Stuck in a local optimum.
因此,与其依赖很差的梯度信号,不如忽略梯度,使用黑盒优化:遗传算法(GA)、进化策略(ES)等,直接把策略/模型当成一个黑盒函数 $f(\theta)$ 来优化。
作者提到了这篇工作:Evolution Strategies as a Scalable Alternative to Reinforcement Learning ,并指出虽然ES效率不如RL,但是它的并行化极其容易。
作者还提到像学习模型结构这样的问题,梯度也无计可施,需要依赖RL,ES,GA
2. Evolution Strategy
ES 是一个提出候选解并根据适应度更新分布的算法。你提供一个目标函数,ES 每一代在自己的一个采样分布中给你一批参数向量让你评估,然后它根据评估结果更新自己的采样分布,迭代直到足够好。
下面是一段伪代码说明:
solver = EvolutionStrategy()
while True:
# ask the ES to give us a set of candidate solutions
solutions = solver.ask()
# create an array to hold the fitness results.
fitness_list = np.zeros(solver.popsize)
# evaluate the fitness for each given solution.
for i in range(solver.popsize):
fitness_list[i] = evaluate(solutions[i])
# give list of fitness results back to ES
solver.tell(fitness_list)
# get best parameter, fitness from ES
best_solution, best_fitness = solver.result()
if best_fitness > MY_REQUIRED_FITNESS:
break
- ES 不一定要把“种群大小”固定死,本质上它在维护一个分布(distribution),每一代从中采样候选解。
- 训练时你只需要能评估
evaluate(θ),不需要梯度,也不需要知道内部结构。
评估函数
作者使用了下面这种有着许多局部最小值的函数去评估ES算法。
 Rastrigin-2D Function的三维示意图
Rastrigin-2D Function的三维示意图
Schaffer-2D Function
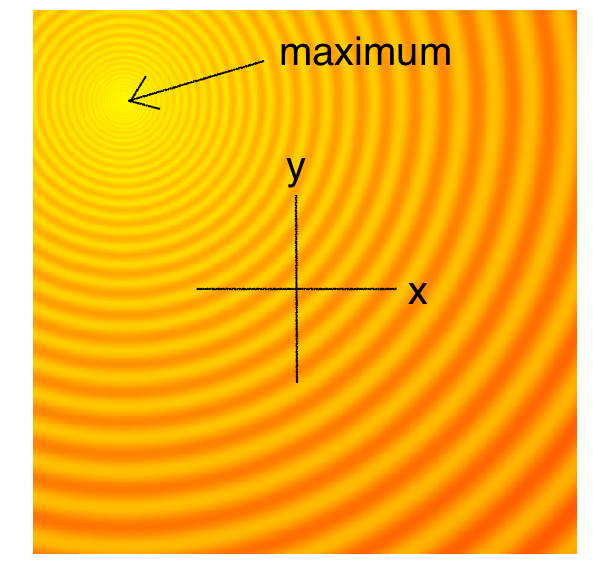 图注:Schaffer 函数具有复杂的波纹结构,许多局部峰值环绕在全局最优周围。
图注:Schaffer 函数具有复杂的波纹结构,许多局部峰值环绕在全局最优周围。
Rastrigin-2D Function
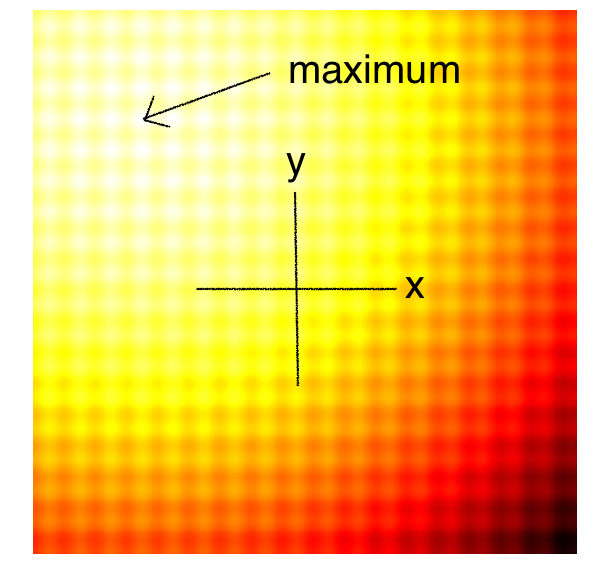 图注:Rastrigin 是非常典型的“多峰”函数,表面布满了像蛋格一样的局部最优陷阱。如果只沿着梯度走,极易卡在任何一个格子里。
图注:Rastrigin 是非常典型的“多峰”函数,表面布满了像蛋格一样的局部最优陷阱。如果只沿着梯度走,极易卡在任何一个格子里。
我们的任务是找到一组参数 $\theta$,使得 $F(\theta)$ 尽可能接近全局最大值。
4. Simple Evolution Strategy
Simple Evolution Strategy,正如其名,是比较简单的Evolution Strategy。它的采样使用正态分布$ \mathcal{N}(\mu, \sigma^2) $,其中标准差$\sigma$是一个固定值。每次选择采样的样本中fitness值最大的样本作为下一次采样的$\mu$。
Schaffer 上的 Simple ES
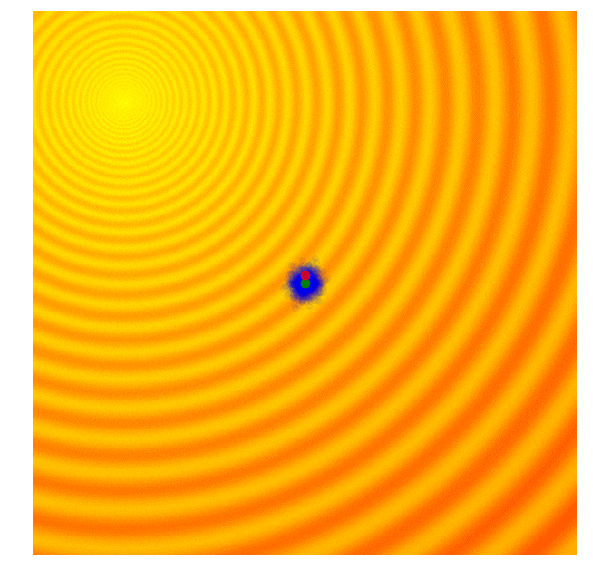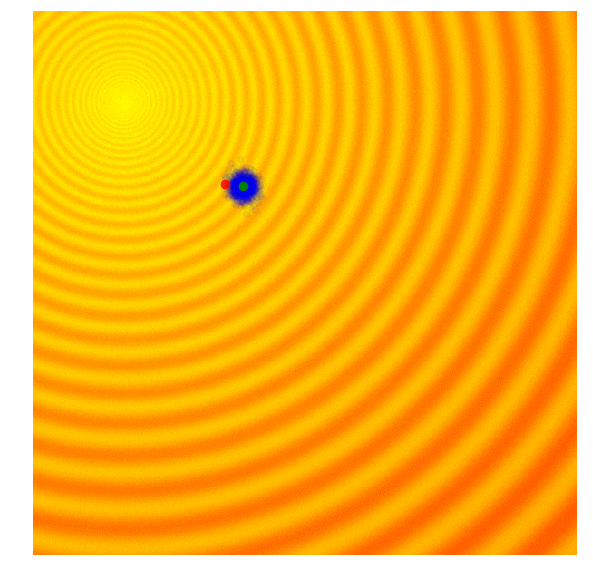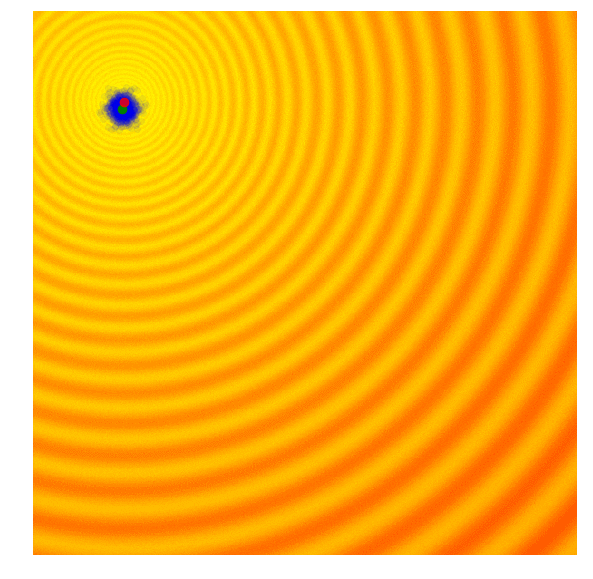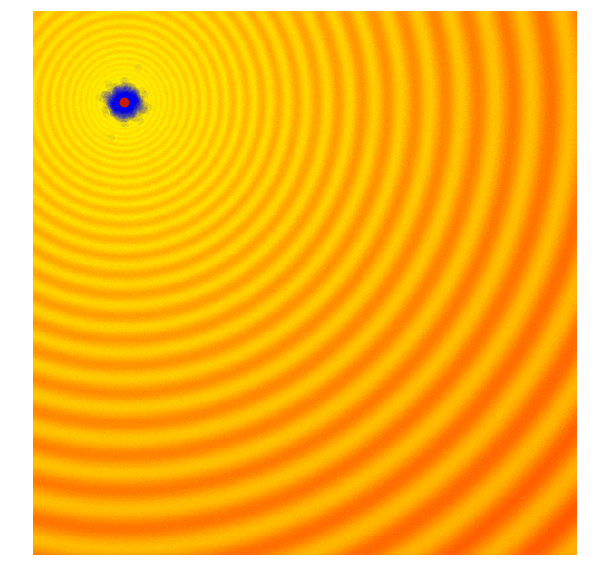
Rastrigin 上的 Simple ES
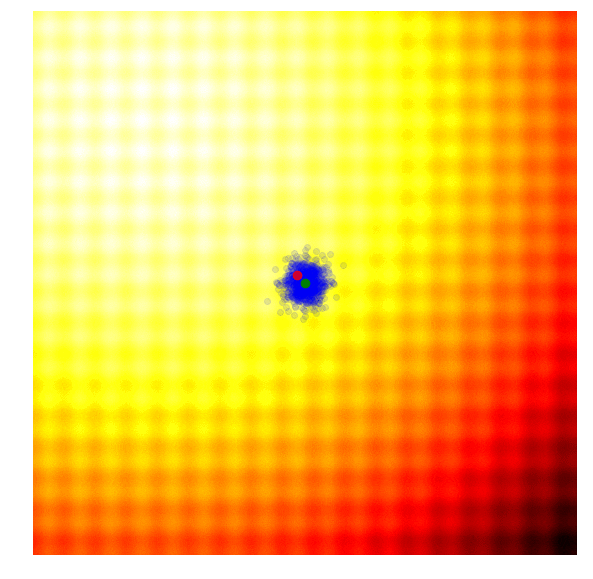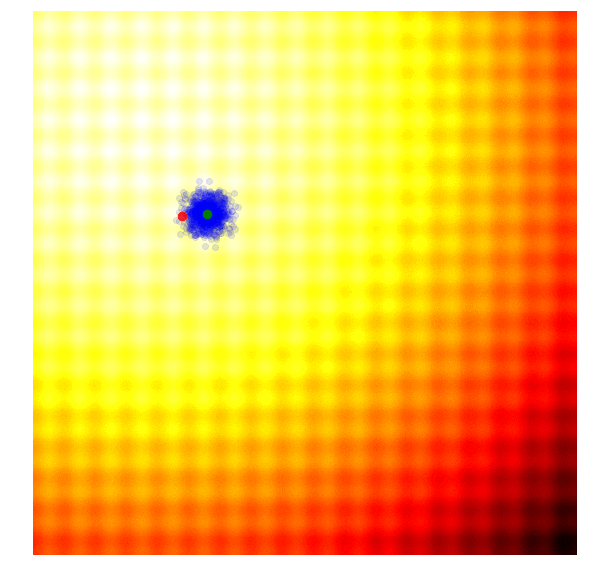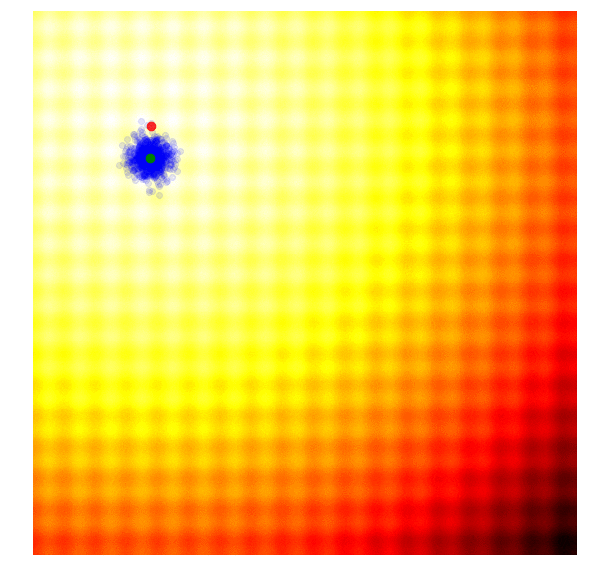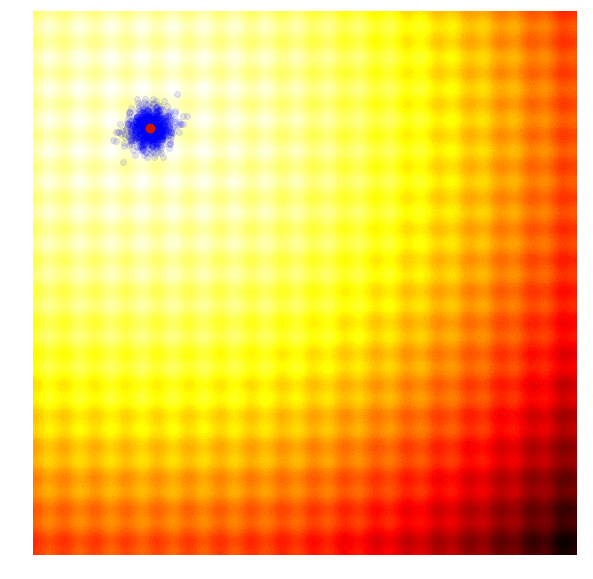
这种方法非常贪心,容易陷入局部最优。作者也如是评价
It would be beneficial to sample the next generation from a probability distribution that represents a more diverse set of ideas, rather than just from the best solution from the current generation.
5. Simple Genetic Algorithm
这是对Simple Evolution Strategy的改进,为了增加多样性,作者引入了经典的遗传算法(GA)思路。这也是最古老的黑盒优化方法之一。
思路是不只选择top-1,而是保留top-10%。下一代采样时,先随机选择两个精英做父母,融合产生后代,再对子代参数加上高斯噪声(同样固定标准差)。
Schaffer 上的 Simple GA
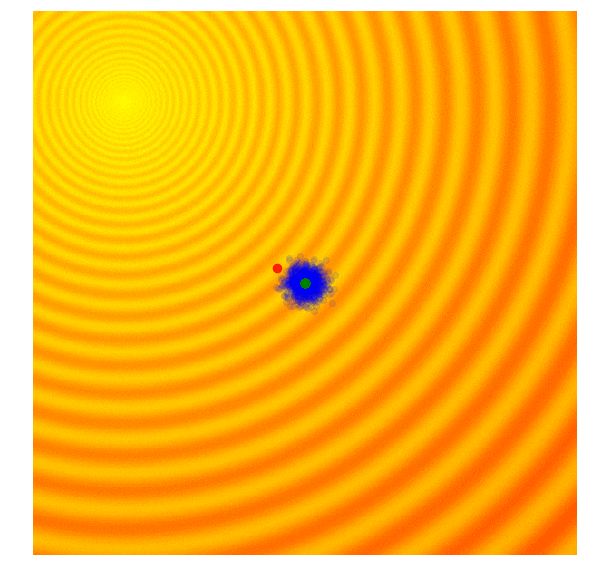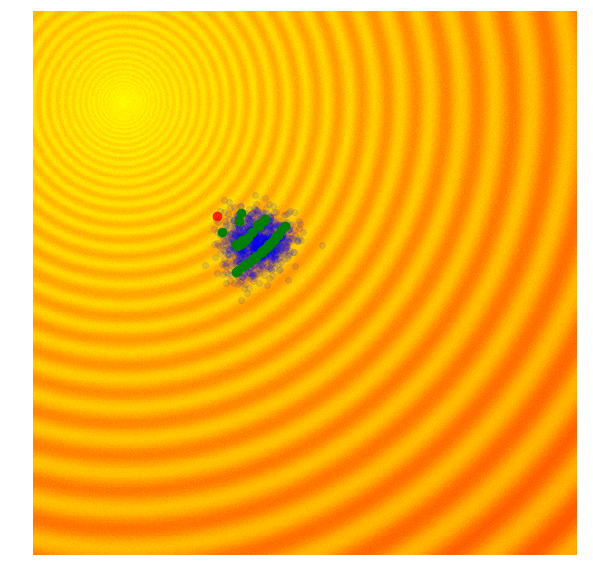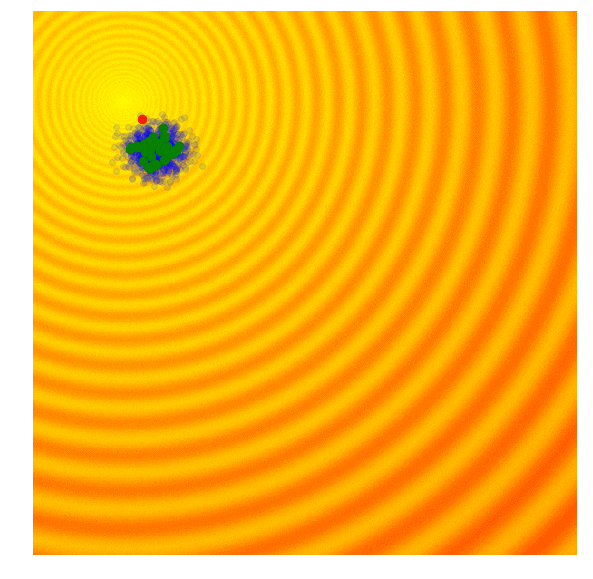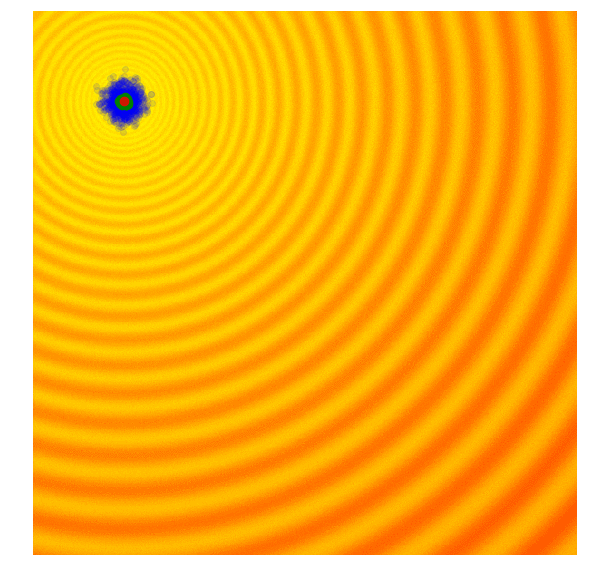
Rastrigin 上的 Simple GA
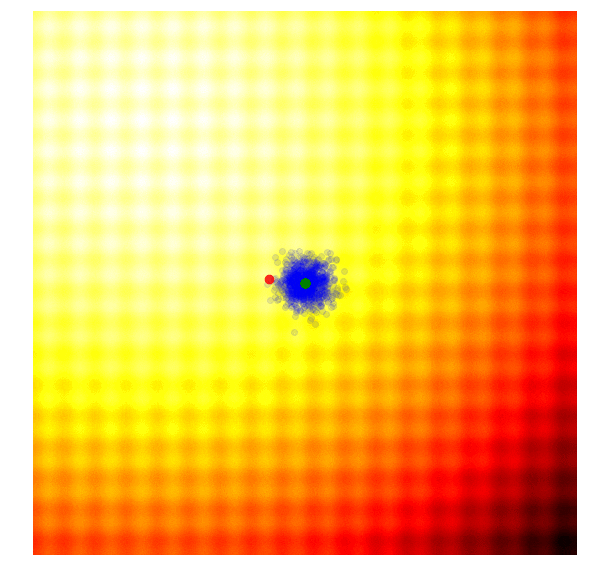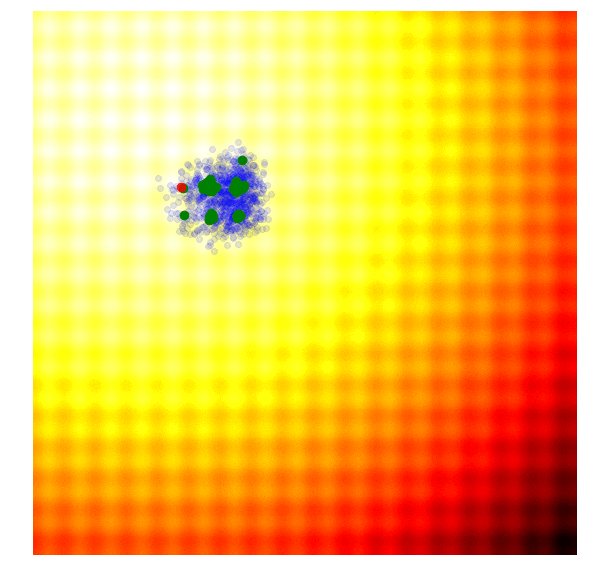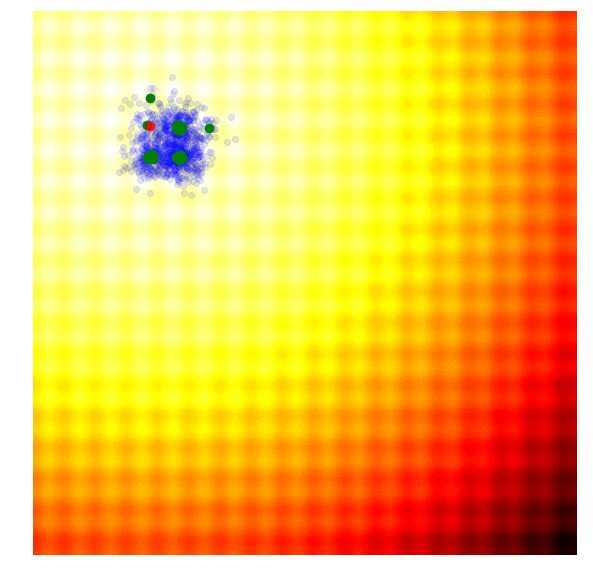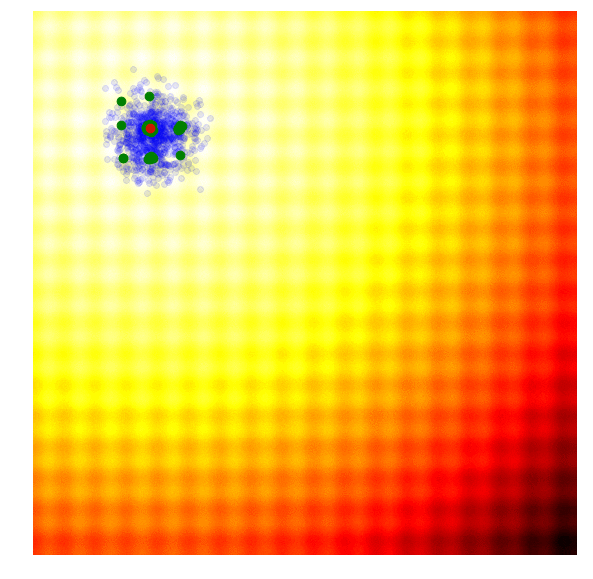
在实践中,精英同样可能趋同,导致陷入局部最优解。GA有一些更复杂的变体如CoSyNe, ESP, NEAT, where the idea is to cluster similar solutions in the population together into different species, to maintain better diversity over time.
6. Covariance-Matrix Adaptation Evolution Strategy (CMA-ES)
Simple ES 和 Simple GA 都有一个共同的缺陷:标准差 $\sigma$ 是固定的。 在搜索过程中,有时我们希望探索更大的范围(增大 $\sigma$),有时在接近最优解时又希望精细微调(减小 $\sigma$)。
CMA-ES 正是解决这个问题的方案。它不仅能自适应调整均值 $\mu$ 和步长 $\sigma$,还能学习参数之间的协方差矩阵(Covariance Matrix)。这意味着它可以改变搜索分布的形状(这就好比从画圆变成画椭圆),顺着山谷的方向进行探索。
Schaffer 上的 CMA-ES
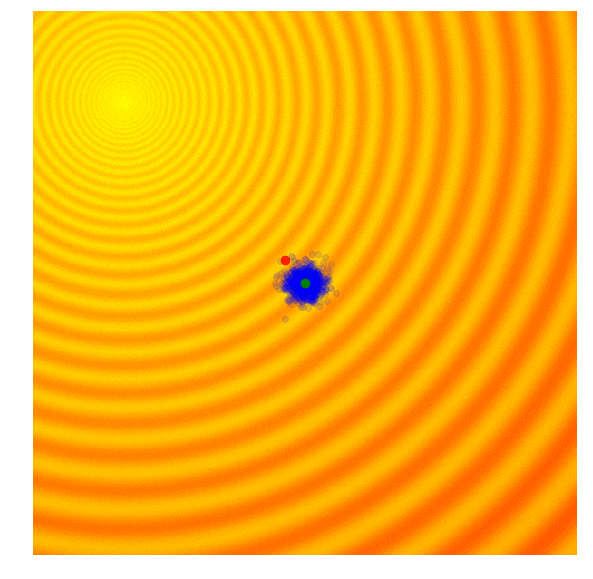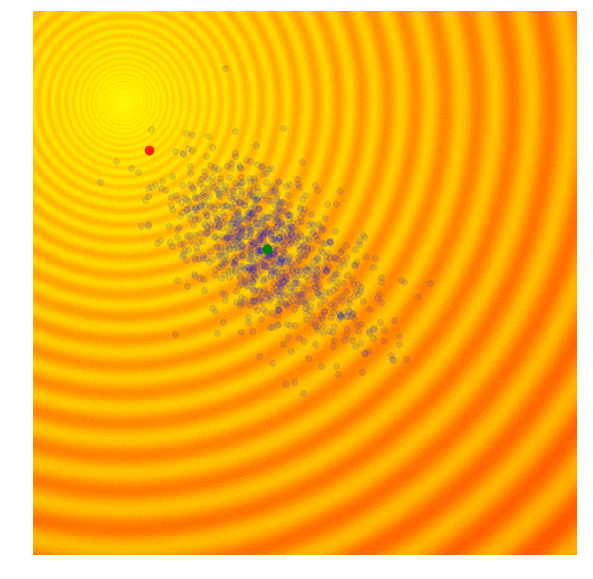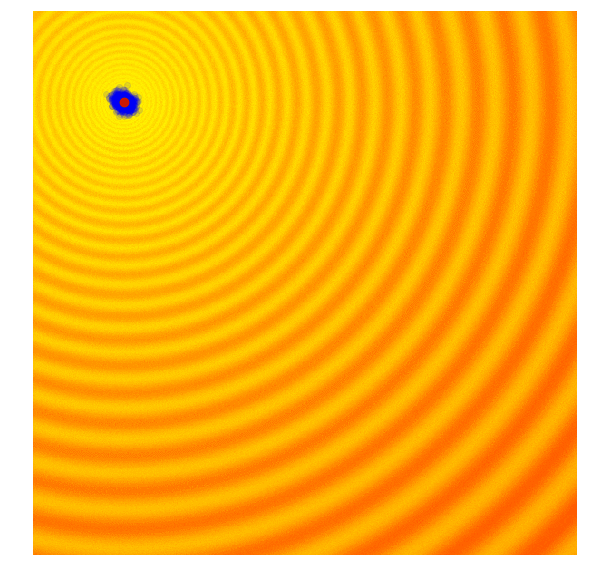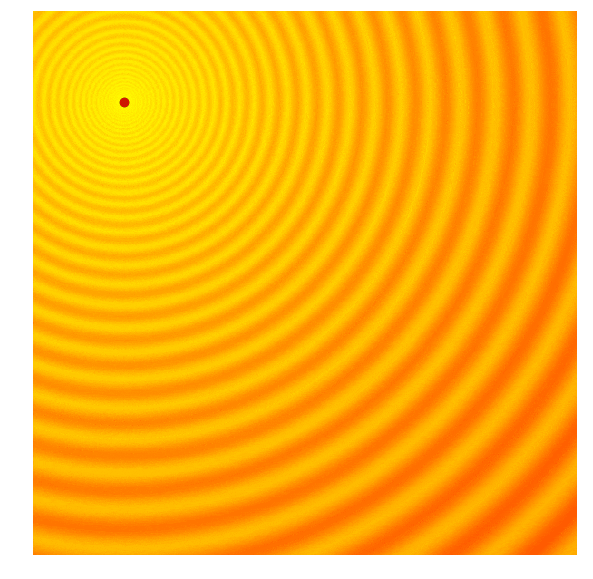
CMA-ES 的核心机制如下:
- 选择精英:根据适应度选择前 $N_{best}$ 个样本(例如前25%)。
- 更新均值:新一代的均值 $\mu^{(g+1)}$ 是这些精英样本的加权平均。
- 更新协方差:利用这一代的精英样本分布,来更新下一代的协方差矩阵 $C^{(g+1)}$。
对于参数 $x, y$,均值更新十分直观: $$ \mu_x^{(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} x_i, \quad \mu_y^{(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} y_i $$
协方差矩阵的估计(简化版)则是计算方差和协方差: $$ \sigma_x^{2 (g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} (x_i - \mu_x^{(g)})^2 $$ $$ \sigma_y^{2 (g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} (y_i - \mu_y^{(g)})^2 $$ $$ \sigma_{xy}^{(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} (x_i - \mu_x^{(g)})(y_i - \mu_y^{(g)}) $$
通过这种机制,CMA-ES 可以自动扩大或缩小搜索范围,甚至旋转搜索方向以适应目标函数的“地形”。它是目前最流行的无梯度优化算法之一,特别适合参数量在中小规模(< 1000)的问题。对于更大的参数量,完整的协方差矩阵计算量 $O(N^2)$ 会过大,此时通常会使用近似版本或者对角化版本。
想要获取更多细节的话,作者推荐了CMA-ES Tutorial。
7. Natural Evolution Strategies (NES)
前面的方法(Simple ES, GA, CMA-ES)大多属于“硬选择”:只保留好的,扔掉坏的。但实际上,表现差的样本也包含了信息——它们告诉了我们“哪里不要去”。
Natural Evolution Strategies (NES) 试图利用整个种群的信息来估计梯度。
7.1 数学推导:从 REINFORCE 到 NES
许多强化学习研究者对 REINFORCE (Williams, 1992) 并不陌生。REINFORCE 论文的第 6 节实际上就提议了将其用作一种“进化策略”。后来的 PEPG (2009) 和 NES (2014) 进一步扩展了这一思想。
核心思想是最大化期望适应度(Expected Fitness):
$$ J(\theta) = \mathbb{E}_{z \sim p(z|\theta)}[F(z)] = \int F(z) p(z|\theta) dz $$
其中 $\theta$ 是我们要优化的分布参数(比如高斯的 $\mu$ 和 $\sigma$),$F(z)$ 是目标函数。 我们想用梯度上升(Gradient Ascent)来最大化 $J(\theta)$。如何求 $\nabla_\theta J(\theta)$ 呢?这里用到了著名的 Log-Likelihood Trick(对数似然技巧):
$$ \begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta \int F(z) p(z|\theta) dz \\ &= \int F(z) \nabla_\theta p(z|\theta) dz \\ &= \int F(z) \frac{\nabla_\theta p(z|\theta)}{p(z|\theta)} p(z|\theta) dz \\ &= \int F(z) \nabla_\theta \log p(z|\theta) p(z|\theta) dz \\ &= \mathbb{E}_{z \sim p(z|\theta)} [F(z) \nabla_\theta \log p(z|\theta)] \end{aligned} $$
这就把梯度的计算转化为了一个期望值,我们可以通过采样 $N$ 个样本来近似这个期望:
$$ \nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N F(z_i) \nabla_\theta \log p(z_i|\theta) $$
这就得到了一个通用的梯度估计器!我们可以像训练神经网络一样,使用 SGD、RMSProp 或 Adam 来更新 $\theta$。
7.2 针对高斯分布的具体推导
假设我们的采样分布是因子分解的高斯分布(Factorized Gaussian): $$ p(z|\theta) = \prod_{j=1}^{d} \frac{1}{\sqrt{2\pi}\sigma_j} \exp\left(-\frac{(z_j - \mu_j)^2}{2\sigma_j^2}\right) $$ 其中 $\theta$ 包含了均值向量 $\mu$ 和标准差向量 $\sigma$。
我们可以分别计算关于 $\mu$ 和 $\sigma$ 的对数似然梯度:
$$ \nabla_{\mu_j} \log p(z|\theta) = \frac{z_j - \mu_j}{\sigma_j^2} $$ $$ \nabla_{\sigma_j} \log p(z|\theta) = \frac{(z_j - \mu_j)^2 - \sigma_j^2}{\sigma_j^3} $$
将这些代入通用的梯度估计公式,我们就可以同时更新均值和方差。这使得算法不仅能寻找最优位置(通过更新 $\mu$),还能像 CMA-ES 一样自适应地调整搜索范围(通过更新 $\sigma$)。
7.3 自然梯度 (Natural Gradient)
NES 中的 "Natural" 指的是它使用了自然梯度(Natural Gradient)。 普通的梯度下降沿着欧几里得空间的梯度方向走,而自然梯度下降沿着分布流形(Riemannian Manifold)的梯度方向走,这通常能带来更快的收敛。
自然梯度的更新公式为: $$ \theta \leftarrow \theta + \alpha \mathbf{F}^{-1} \nabla_\theta J(\theta) $$ 其中 $\mathbf{F}$ 是 Fisher Information Matrix。
在完全的 NES 中,我们需要计算并求逆这个 Fisher 矩阵。不过在很多简化版本(如 PEPG 或 OpenAI ES)中,我们往往假设 $\sigma$ 固定或者使用对角近似,从而避免了昂贵的矩阵运算。
Schaffer 上的 NES (PEPG)
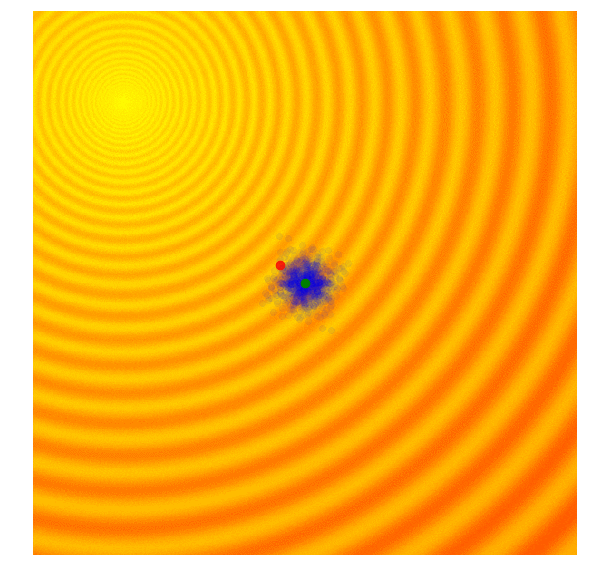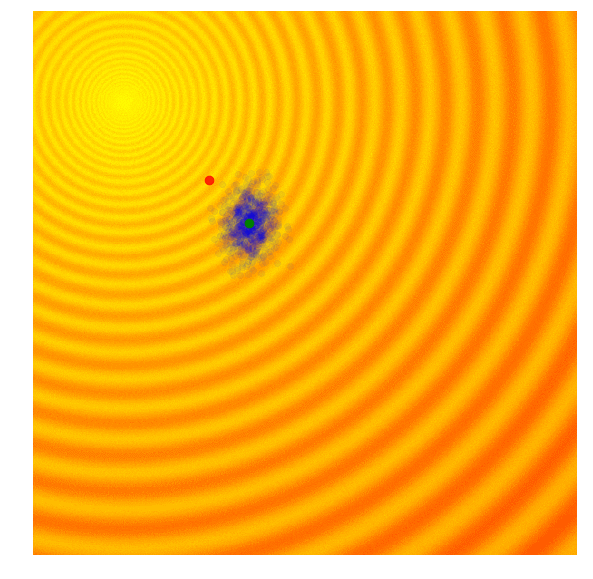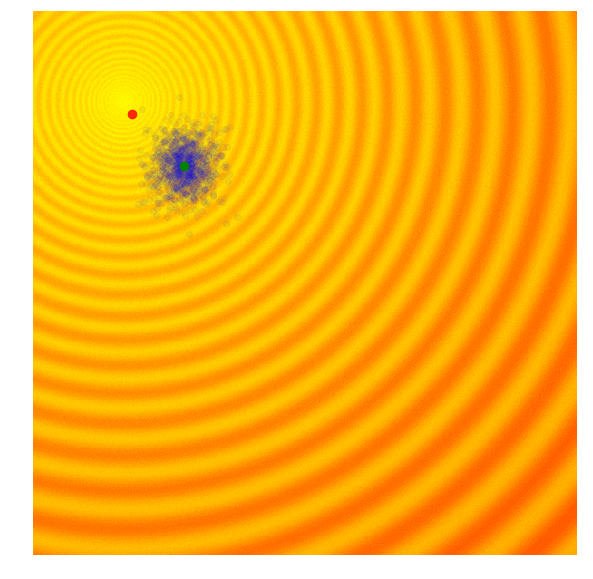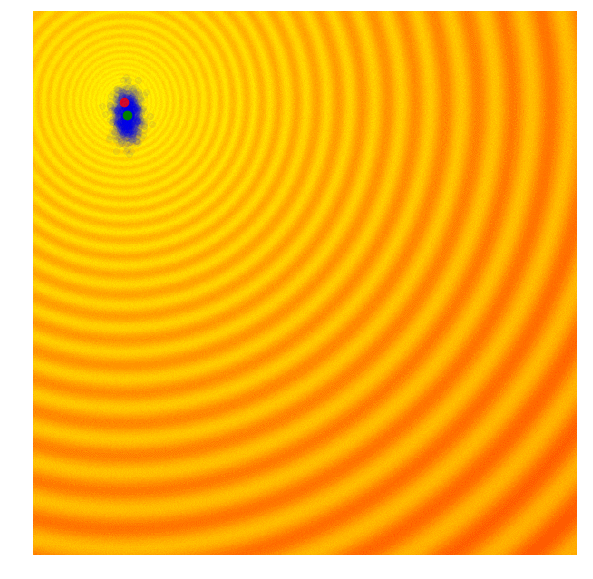
Rastrigin 上的 NES (PEPG)
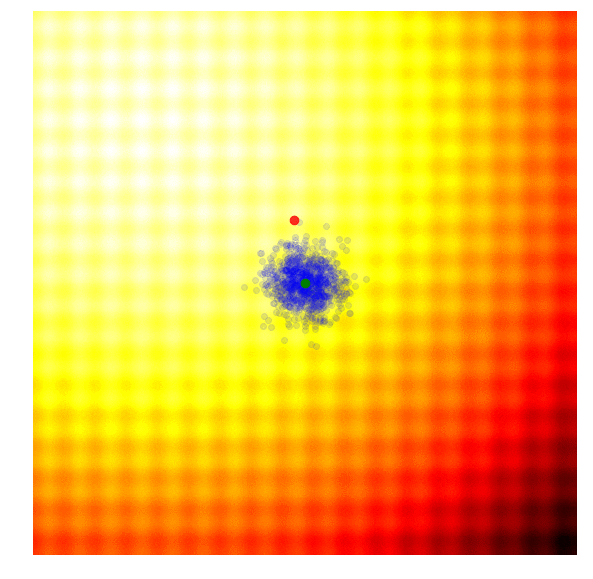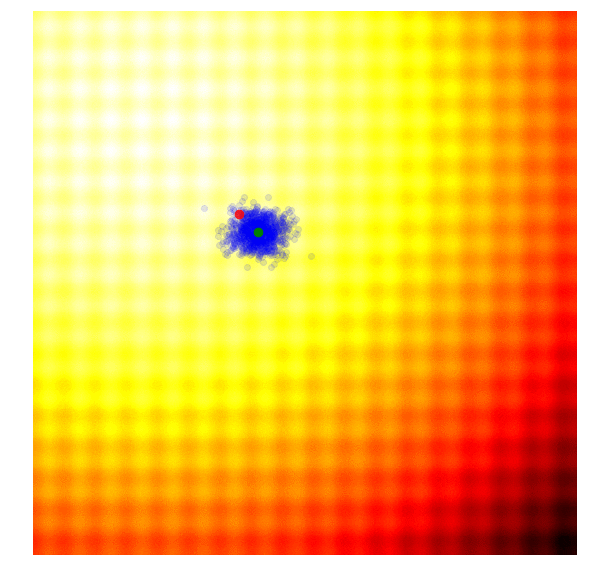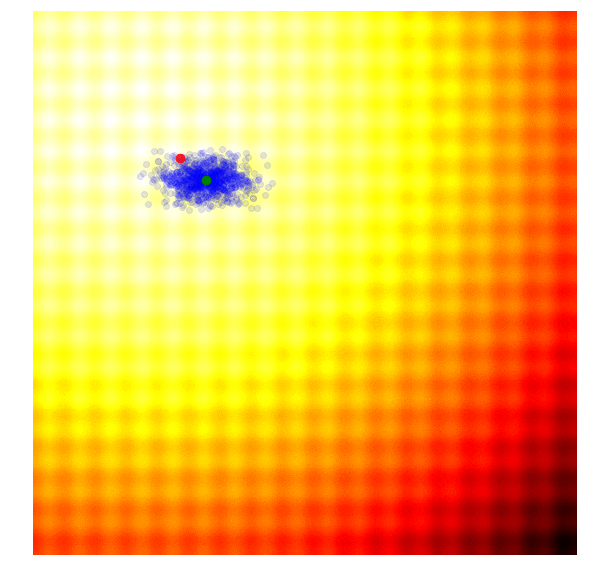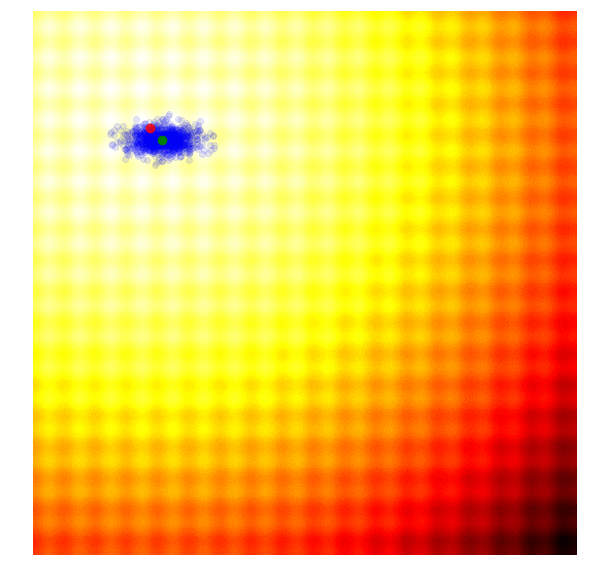
(注:上图展示的是 PE-PG (Parameter-Exploring Policy Gradients),它是 NES 的一种变体,效果非常稳健。)
8. OpenAI Evolution Strategy
OpenAI 在 2017 年发表的 Evolution Strategies as a Scalable Alternative to Reinforcement Learning 中使用了一种特殊的 ES。 本质上,它是 NES 的一个特例。
OpenAI 的版本做了一个重要简化:固定标准差 $\sigma$ 不变,只更新均值 $\mu$。 假设分布是各向同性的高斯分布 $p(z|\mu) = \mathcal{N}(\mu, \sigma^2 I)$,那么 $\nabla_\mu \log p(z|\mu)$ 就是:
$$ \nabla_\mu \log p(z|\mu) = \frac{z - \mu}{\sigma^2} $$
如果我们令 $z_i = \mu + \sigma \epsilon_i$(其中 $\epsilon_i \sim \mathcal{N}(0, I)$),代入上面的梯度公式,就会得到 OpenAI ES 的核心更新公式:
$$ \nabla_\mu J(\theta) \approx \frac{1}{N\sigma} \sum_{i=1}^N F(\mu + \sigma \epsilon_i) \epsilon_i $$
这其实就是:如果在 $\epsilon_i$ 方向上 $F$ 值高,我们就往 $\epsilon_i$ 方向走一点;如果低,就往反方向走。
OpenAI ES 的并行化优势 OpenAI 强调这个算法非常适合大规模并行计算。 在分布式训练中,通常需要传输巨大的参数梯度。但在 ES 中,我们可以利用随机数种子(Seed)的技巧: 1. 所有的 Worker 预先约定好随机数生成方式。 2. Master 只需要发送一个 Seed 给 Worker。 3. Worker 根据 Seed 还原出扰动 $\epsilon_i$,计算 fitness $F(\mu + \sigma \epsilon_i)$。 4. Worker 只需要把算出来的 scalar(一个数字,即 fitness) 传回给 Master。 5. Master 聚合这些标量,自己就可以根据 Seed 重建 $\epsilon_i$ 并完成梯度更新。
这使得通信带宽需求极低,可以轻松扩展到成千上万个 CPU 核心。
9. Fitness Shaping
为了让算法更鲁棒,通常不直接使用原始的 $F(z)$ 值,而是使用 Rank(排名)。 比如有 100 个样本,我们按 $F(z)$ 从小到大排序。 - 排名第一的赋分 $0.5$ - 排名最后的赋分 $-0.5$ - 中间的线性插值
这种 Fitness Shaping 有两个好处: 1. 抗离群值:如果某个样本的 Fitness 异常大(Outlier),直接求和会带偏梯度,用排名则不会。 2. 梯度稳定:无论目标函数 $F$ 的数值范围是多少,优化器的梯度幅值都保持稳定。
10. MNIST 实验
作者在一个小型的卷积神经网络(约 11k 参数)上测试了各种 ES 方法来分类 MNIST。虽然这类监督学习问题绝对是反向传播(Backprop)的主场,但用 ES 来做可以测试其优化能力。
结果如下(迭代 300代):
| Method | Train Accuracy | Test Accuracy |
|---|---|---|
| Adam (Backprop) | 99.8% | 98.9% |
| Simple GA | 82.1% | 82.4% |
| CMA-ES | 98.4% | 98.1% |
| OpenAI ES | 96.0% | 96.2% |
| PEPG (NES) | 98.5% | 98.0% |
可以看到,CMA-ES 和 NES (PEPG) 都能达到约 98% 的准确率,非常接近基于梯度的 Adam 优化器!这证明了对于中小规模参数的模型,高级的 ES 算法确实有很强的优化能力。
11. 总结
- 什么时候用 ES?
- 当没有梯度信息(如 RL,或者不可导的模拟器)时。
- 当目标函数充满了局部最优和噪声,需要全局探索时。
-
当你需要极大规模并行,且参数量不是特别巨大时。
-
梯度法 vs 进化策略
- 梯度法(Backprop/SGD):在参数空间通过梯度“滑”向谷底。效率高,但怕局部最优。
- 进化策略(ES):在参数空间维护一个分布,通过采样“摸索”整体地形。更鲁棒,但采样效率低(Sample Inefficient)。
David Ha 最后总结道:虽然 ES 目前在数据效率上不如 RL 算法(如 A3C, PPO),但随着计算能力的提升和并行化的普及,ES 作为一种简单暴力的黑盒优化手段,在未来仍有巨大的潜力。
12. 自行尝试
CMA-ES的作者使用numpy实现了CMA-EA,位于https://github.com/CMA-ES/pycma。