Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning

作者: Felipe Petroski Such, Vashisht Madhavan, Edoardo Conti, Joel Lehman, Kenneth O. Stanley, Jeff Clune (Uber AI Labs)

论文链接: http://arxiv.org/abs/1712.06567v3

写在前面

这篇工作算是GA中比较经典的一篇工作了，代码开源在https://github.com/uber-research/deep-neuroevolution，可以找时间阅读复现一下。

引言

本文简单来说就是把Genetic Algorithm（GA）应用在了一些强化学习benchmark上，并发现其能力可以与传统算法（A3C, DQN, and ES）匹敌。

然后把GA和random search（RS）去比较，证明了其有效性。作者在这个过程中意外发现了RS在一些任务上的表现比传统算法还要好。

方法

GA

Genetic Algorithm（GA）就无需多言了，值得一提的是这篇文章中作者舍弃了选择两个/多个parents杂交的操作。具体流程大致如下：

在第 $n=1$ 代，随机初始化 $N$ 个个体。初始化方法记作函数 $\phi$。初始化种子记为$\tau_0$。 $$ \theta^{0} = \phi(\tau_0) $$
适应度评估
根据适应度 $F_i$ 对种群进行排序。选择适应度最高的 $T$ 个个体作为父代，用于产生下一代。
使用父代的 $T$ 个个体，产生下一代的 $N$个个体。首先重复以下步骤 $N-1$ 次：
1. 从 $T$ 个父代中均匀随机地（有放回）选择一个父代 $\theta^{n-1}$。
2. 对父代参数添加高斯噪声来生成子代 $\theta^{n}$： $$ \theta^n = \psi(\theta^{n-1}, \tau_n) = \theta^{n-1} + \sigma \epsilon(\tau_n) \tag{1} $$ 其中 $\epsilon \sim \mathcal{N}(0, I)$ 是采样自标准正态分布的噪声向量，$\sigma$ 是控制变异强度的超参数（由经验确定，可见原文的附录）。
为了防止最优解丢失，下一代中的第 $N$ 个个体直接复制上一代中适应度最高的个体。这里为了在噪声环境中准确的找出“真正的”精英，作者对 Top 10 个体进行额外的 30 次评估取平均。 > To more reliably try to select the true elite in the presence of noisy evaluation, we evaluate each of the top 10 individuals per generation on 30 additional episodes (counting these frames as ones consumed during training); the one with the highest mean score is the designated elite.

压缩参数

同时本文提出了一个压缩存储模型参数的方法，即使用种子的序列去保存模型的参数。根据上面的GA方法，不难看出：任意第 $n$ 代的个体 $\theta^n$ 可以完全由一个种子序列重构： $$ \tau_{sequence} = (\tau_0, \tau_1, \dots, \tau_n) $$ 通过从 $\theta^0$ 开始依次应用公式 (1)，可以完全还原出巨大的神经网络权重，而数据量仅为 $n$ 个整数。

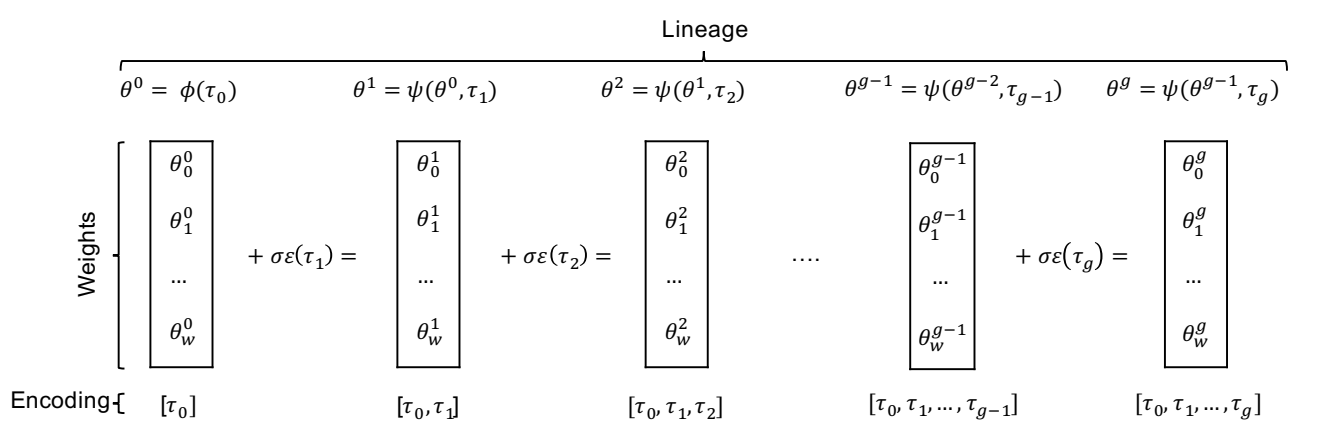
GA 编码方法

新颖性搜索

文中还提到了一个避免陷入局部最优解的新颖性搜索方法，可见原文。

实验

Atari 2600 游戏

在 13 款 Atari 游戏中对比了 GA 与 DQN, A3C, ES 以及随机搜索（RS）的表现。使用的是与 DQN 相同的网络架构（3层卷积+全连接，4M+参数）。

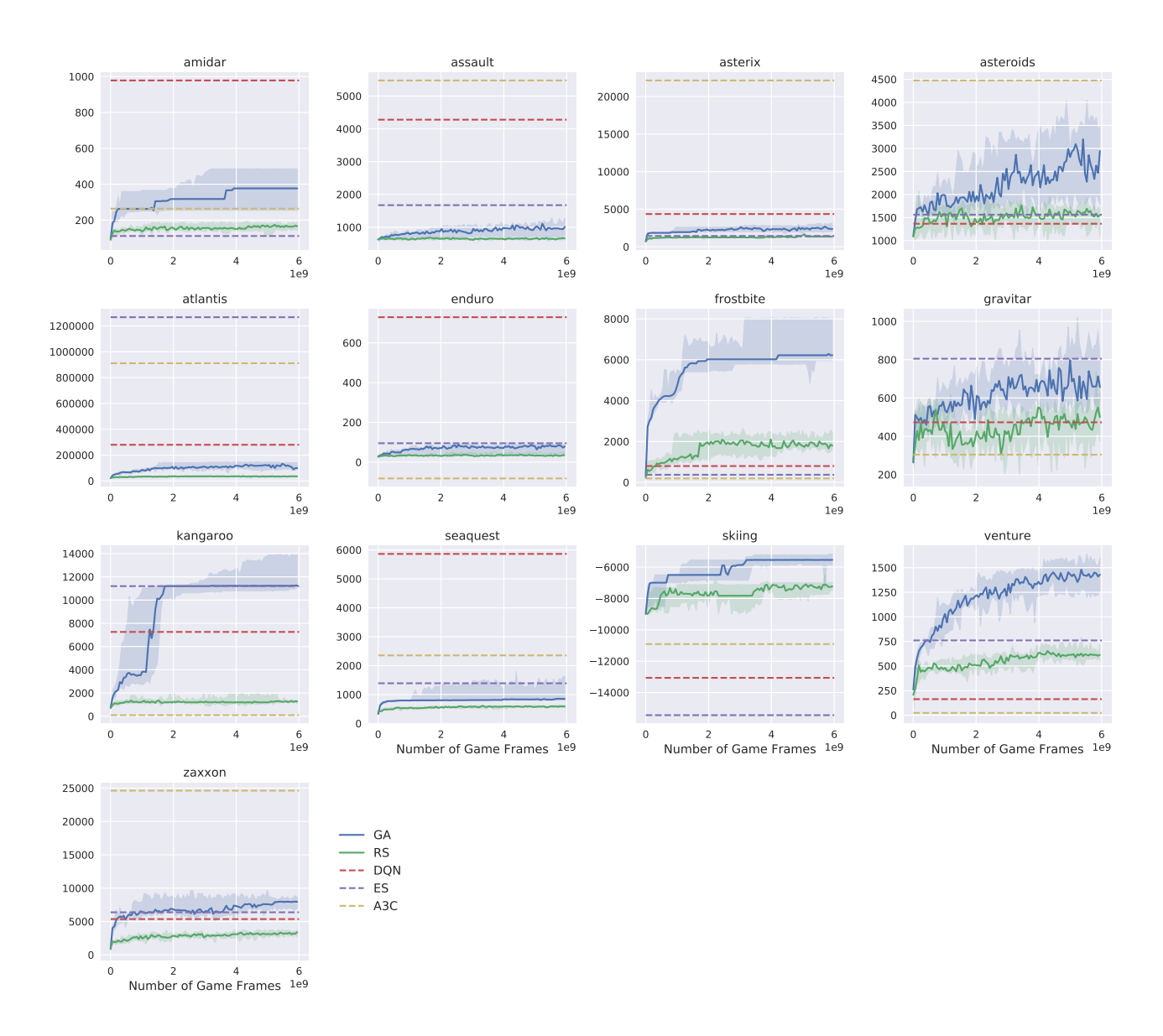
Atari 性能对比曲线

结果：
- GA 在 13 个游戏中的表现与 DQN, A3C, ES 处于同一水平线。
- 在 Skiing, Frostbite, Venture 等游戏中，GA 表现优异，甚至超过了当时的 SOTA。
- 随机搜索 (RS)：令人惊讶的是，RS 在 Frostbite, Skiing 和 Venture 上击败了 DQN；在 6 个游戏中击败了 A3C。这表明这些游戏的某些“困难”可能更多是由于梯度优化的陷阱，而非策略本身的搜索空间难以触达。

下图展示了随机搜索在 Frostbite 中发现的一个复杂策略： Frostbite 随机搜索策略 (该策略能完成一系列连贯动作：跳下移动的冰山、建造冰屋、进入冰屋获取奖励，这通常被认为是需要长期规划的任务。)

图像硬迷宫 (Image Hard Maze) - 欺骗性问题

这是一个经典的具有欺骗性奖励的迷宫问题。机器人需要到达终点，但贪婪地通过奖励（距离目标的距离）优化会导致机器人陷入死胡同（Trap）。本文将其升级为基于像素输入的深度学习版本。

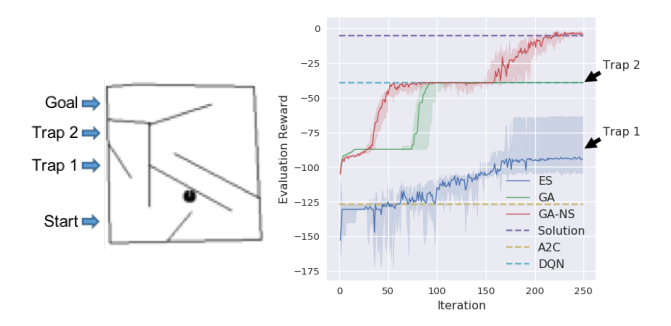
Image Hard Maze 实验结果

左图：迷宫俯视图。机器人从左下角出发，目标在左上角。直接向上走会进入 Trap 2（局部最优）。
右图：不同算法的路径探索情况。
- GA, ES, DQN, A2C：均失败。它们都试图最大化奖励，结果被困在 Trap 2 或其他局部最优。
- GA-NS (Novelty Search)：成功。因为它不依赖奖励，而是探索未知的状态空间，最终绕过陷阱找到了目标。
结论：证明了进化算法特有的探索机制（如新颖性搜索）可以有效解决深度强化学习中的欺骗性问题。

人形机器人行走

在 MuJoCo 物理引擎中测试了连续控制任务。 * 结果：GA 最终能够学会行走（得分 > 6000），解决了该问题。 * 对比：相比 ES，GA 在此任务上需要的计算量大得多（约 15 倍）。这表明 GA 并非在所有领域都优于或等同于基于梯度的通过（ES 使用了近似梯度）。

讨论

梯度的必要性？：GA 和随机搜索的成功表明，在某些高维参数空间中，并不一定需要跟随梯度才能找到优秀的解。在原点附近的密集采样（随机搜索）或局部邻域采样（GA）有时比梯度下降更有效，尤其是在梯度存在噪声或误导性的情况下。
局部最优与鞍点：梯度方法容易陷入鞍点或局部最优，而 GA 可以通过参数空间的跳跃来逃离这些区域。
时间扩展探索 (Temporally Extended Exploration)：GA/ES 在整个 episode 中保持参数不变，这种一致性的探索可能比每步都改变策略（如某些基于梯度的 RL）更有利于信贷分配（Credit Assignment）。
混合算法的潜力：结果激励了混合算法的研究，例如结合 GA 的探索能力和梯度方法的精细优化能力，或者将新颖性搜索（NS）与深度 RL 算法结合。

结论

本文通过 Deep GA 证明了遗传算法是训练深度神经网络解决强化学习问题的有力竞争者。 * 有效性：在 Atari 和 Humanoid 任务上表现出与 SOTA 深度 RL 算法相当的性能。 * 效率：具有极高的并行效率，能在数小时内训练 Atari 模型。 * 工具扩展：开启了将神经进化领域的丰富工具库（如新颖性搜索、间接编码等）应用于深度学习的大门。 * 启示：挑战了“深度学习必须依赖梯度”的传统观念，表明简单的旧算法配合现代算力也能产生惊人的效果。