Evolution Strategies as a Scalable Alternative to Reinforcement Learning

作者: Tim Salimans, Jonathan Ho, Xi Chen, Szymon Sidor, Ilya Sutskever (OpenAI)

论文链接: http://arxiv.org/abs/1703.03864v2

日期：2017年9月7日

被引用：2111（来自谷歌学术）

1. 引言

在强化学习 (RL) 领域，基于马尔可夫决策过程 (MDP) 的算法（如 Q-learning 和 策略梯度）是主流范式。然而，本文探索了一种替代方案：进化策略 (Evolution Strategies, ES)。

ES 是一类黑盒优化算法。本文证明了 ES 可以可靠地训练深度神经网络策略，并且非常适合现代分布式计算系统。

核心发现

1. 网络参数化的重要性：使用虚拟批归一化 (Virtual Batch Normalization, VBN) 等技术极大地提高了 ES 的可靠性。
2. 高度并行化：通过一种基于公共随机数 (Common Random Numbers) 的通信策略，ES 可以在数千个 CPU 上实现线性加速。
3. 数据效率与计算效率：虽然 ES 的数据效率（Data Efficiency）比 A3C 低 3-10 倍，但由于不需要反向传播和价值函数近似，计算量减少了约 3 倍。在墙钟时间 (Wall-clock time) 上，ES 极具竞争力（例如，1 小时训练 Atari 相当于 A3C 的 1 天）。
4. 探索行为：ES 表现出与策略梯度（如 TRPO）截然不同的探索行为，能够发现更多样的步态（如侧向行走或倒退）。
5. 鲁棒性：ES 在所有 Atari 游戏中使用固定的超参数，在 MuJoCo 任务中也几乎使用统一的超参数。

2. 方法

2.1 基础原理

ES 属于自然进化策略 (NES) 的一种。我们的目标是最大化目标函数 $F(\theta)$ 的期望值，其中 $\theta$ 是策略网络的参数。

为了处理不可导或非平滑的目标函数（RL 环境通常如此），ES 对参数 $\theta$ 引入高斯噪声进行平滑。定义平滑后的目标函数为参数分布 $p_\psi$ 下的期望： $$ J(\theta) = \mathbb{E}_{\theta \sim p_{\psi}} F(\theta) = \mathbb{E}_{\epsilon \sim N(0,I)} F(\theta + \sigma \epsilon) $$

这里标准差$\sigma$是我们的超参数。现在我们来算目标函数的梯度。

设 $\tilde{\theta} = \theta + \sigma \epsilon$，则 $\tilde{\theta} \sim N(\theta, \sigma^2 I)$。其概率密度函数为： $$ p(\tilde{\theta}; \theta) = \frac{1}{(2\pi)^{d/2}\sigma^d} \exp\left(-\frac{1}{2\sigma^2}\|\tilde{\theta} - \theta\|^2\right) $$

$$ \nabla_\theta \log p(\tilde{\theta}; \theta) = \frac{1}{\sigma^2}(\tilde{\theta} - \theta) = \frac{1}{\sigma^2}(\sigma \epsilon) = \frac{\epsilon}{\sigma} $$

于是我们有 $$ \begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta \int F(\tilde{\theta}) p(\tilde{\theta}; \theta) d\tilde{\theta} \\ &= \int F(\tilde{\theta}) \nabla_\theta p(\tilde{\theta}; \theta) d\tilde{\theta} \\ &= \int F(\tilde{\theta}) p(\tilde{\theta}; \theta) \nabla_\theta \log p(\tilde{\theta}; \theta) d\tilde{\theta} \\ &= \mathbb{E}_{\tilde{\theta} \sim p(\cdot; \theta)} [F(\tilde{\theta}) \nabla_\theta \log p(\tilde{\theta}; \theta)] \\ &= \mathbb{E}_{\epsilon \sim N(0, I)} \left[ F(\theta + \sigma \epsilon) \frac{\epsilon}{\sigma} \right] \end{aligned} $$

最后有 $$ \boxed{ \nabla_{\theta} \mathbb{E}_{\epsilon \sim N(0,I)} F(\theta + \sigma \epsilon) = \frac{1}{\sigma} \mathbb{E}_{\epsilon \sim N(0,I)} \{ F(\theta + \sigma \epsilon) \epsilon \} } $$

2.2 算法流程

对于上面的$\frac{1}{\sigma} \mathbb{E}_{\epsilon \sim N(0,I)} \{ F(\theta + \sigma \epsilon) \epsilon \}$我们可以通过采样平均近似。

1. 输入：学习率 $\alpha$，噪声标准差 $\sigma$，初始参数 $\theta_0$
2. 循环：
   • 采样 $n$ 个噪声向量 $\epsilon_1, \dots, \epsilon_n \sim \mathcal{N}(0, I)$
   • 计算每个扰动参数的回报 $F_i = F(\theta_t + \sigma \epsilon_i)$
   • 更新参数：$\theta_{t+1} \leftarrow \theta_t + \alpha \frac{1}{n\sigma} \sum_{i=1}^n F_i \epsilon_i$

2.3 扩展与并行化 (Scaling and Parallelizing)

ES 非常适合并行化，原因在于我们可以利用公共随机数种子来避免传输巨大的梯度向量。

定义 Worker $i \in \{1, \dots, N\}$，每个 Worker 都有相同的初始参数 $\theta_t$ 和相同的伪随机数生成器状态。

1. 同步：所有 Worker $i$ 同步随机种子 $S_t$。
2. 生成扰动： $$ \epsilon_i(S_t) \sim \mathcal{N}(0, I) $$ 这里 $\epsilon_i$ 是通过种子 $S_t$ 确定的确定性函数。Worker $i$ 只需要知道自己的索引 $i$ 和种子 $S_t$ 即可生成自己的 $\epsilon_i$。
3. 评估：Worker $i$ 在环境中执行策略 $\pi(\cdot; \theta_t + \sigma \epsilon_i)$，获得标量回报 $R_i = F(\theta_t + \sigma \epsilon_i)$。
4. 通信：Worker $i$ 将标量 $R_i$ 广播给所有其他 Worker。这只需要传输 $N$ 个浮点数，而不是 $N$ 个参数维度大小的向量。
5. 重构与更新：每个 Worker $j$ 收到所有 $R_i$ 后，本地重构所有扰动 $\epsilon_i(S_t)$（因为种子已知），并计算全局梯度估计： $$ g_t = \frac{1}{N\sigma} \sum_{i=1}^N R_i \epsilon_i $$ 然后更新参数：$\theta_{t+1} = \theta_t + \alpha g_t$。

这种方法将通信复杂度从 $O(D)$（参数维度）降低到了 $O(N)$（Worker 数量），实现了线性加速。

算法 2：并行化进化策略 * 输入: 学习率 $\alpha$, 噪声标准差 $\sigma$, 初始参数 $\theta_0$, Worker 数量 $N$. * 循环 $t=0, 1, 2, \dots$: * 并行执行 (每个 Worker $i$): * 从公共种子生成扰动 $\epsilon_i \sim \mathcal{N}(0, I)$. * 计算回报 $F_i = F(\theta_t + \sigma \epsilon_i)$. * 广播标量 $F_i$ 给所有其他 Worker. * 并行更新 (每个 Worker $i$): * 接收所有 $\{F_j\}_{j=1}^N$. * 利用种子重构所有 $\{\epsilon_j\}_{j=1}^N$. * $\theta_{t+1} \leftarrow \theta_t + \alpha \frac{1}{N\sigma} \sum_{j=1}^N F_j \epsilon_j$.

2.4 网络参数化 (Network Parameterization)

在 Atari 等视觉任务中，策略网络的输出分布通常对参数非常敏感。为了稳定训练，本文引入了虚拟批归一化 (Virtual Batch Normalization, VBN)。

标准的批归一化 (Batch Normalization, BN) 依赖于当前 mini-batch 的统计量，这在 ES 中会引入额外的随机性（因为输入分布随策略变化）。VBN 通过使用一个固定的参考批次来解决这个问题。

数学形式化： 1. 参考批次 (Reference Batch)：在训练开始前，采样并固定一个输入批次 $X_{ref} = \{x^{(1)}, \dots, x^{(M)}\}$。 2. 统计量计算： 计算 $X_{ref}$ 的均值 $\mu(X_{ref})$ 和标准差 $\sigma(X_{ref})$： $$ \mu_j(X_{ref}) = \frac{1}{M} \sum_{k=1}^M x_j^{(k)}, \quad \sigma_j(X_{ref}) = \sqrt{\frac{1}{M} \sum_{k=1}^M (x_j^{(k)} - \mu_j)^2 + \epsilon} $$ 3. 归一化变换： 对于任意新的输入 $x$，使用固定的参考统计量进行归一化： $$ \hat{x} = \frac{x - \mu(X_{ref})}{\sigma(X_{ref})} $$ 然后应用仿射变换：$y = \gamma \hat{x} + \beta$，其中 $\gamma, \beta$ 是可学习参数。

这种参数化方式使得策略 $\pi(x; \theta)$ 对输入尺度的变化具有不变性，并且在探索初期（参数随机扰动时）能产生更多样化的动作分布，从而避免陷入局部最优（如始终输出同一种动作）。

3. ES 与 策略梯度 (Policy Gradients) 的对比

为什么选择 ES 而不是 Policy Gradients (PG)？

3.1 平滑方式的差异

• PG：在动作空间 (Action Space) 添加噪声（例如 Softmax 采样）。 $$ \nabla_{\theta} F_{PG}(\theta) = \mathbb{E}_{\epsilon} \{ R(\mathbf{a}) \nabla_{\theta} \log p(\mathbf{a}; \theta) \} $$
• ES：在参数空间 (Parameter Space) 添加噪声。 $$ \nabla_{\theta} F_{ES}(\theta) = \mathbb{E}_{\xi} \{ R(\mathbf{a}) \nabla_{\theta} \log p(\tilde{\theta}; \theta) \} $$

3.2 方差分析与长视界 (Long Horizons)

PG 的梯度方差随着时间步 $T$ 线性增长（因为 $\log p(\mathbf{a})$ 是 $T$ 个动作概率之和）。为了减少方差，PG 通常需要折扣因子 (Discounting) 或价值函数 (Value Function)，但这会引入偏差。

ES 的优势： * ES 的梯度项 $\nabla_{\theta} \log p(\tilde{\theta})$ 与时间步 $T$ 无关。 * 因此，ES 特别适合长视界 (Long Horizons)、稀疏奖励以及动作具有长期影响的任务。

3.3 黑盒优化的其他优势

• 不需要反向传播：节省约 2/3 的计算量，节省显存。
• 鲁棒性：避免了 RNN 中的梯度爆炸问题。
• 硬件友好：适合低精度计算和 TPUs。
• 对动作频率不敏感：在 RL 中 Frame-skip 是关键参数，而 ES 对此具有不变性。

4. 实验 (Experiments)

4.1 MuJoCo 控制任务

与 TRPO (Trust Region Policy Optimization) 进行对比。 * ES 能够解决所有测试的 MuJoCo 任务，达到与 TRPO 相当的最终性能。 * 数据效率：在简单任务上 ES 甚至比 TRPO 更快；在困难任务（如 Humanoid）上，ES 需要的数据量大约是 TRPO 的 10 倍。但考虑到 ES 可以大规模并行，其实际训练时间可能更短。

4.2 Atari 游戏

在 51 个 Atari 游戏上测试 ES，训练 10 亿帧。 * 训练时间：使用 720 个 CPU 核，仅需 1 小时 即可完成训练（对比 A3C 需要 1 天）。 * 性能：在 23 个游戏中优于 A3C，28 个游戏中差于 A3C。

4.3 并行化扩展性 (Parallelization)

这是本文最震撼的实验结果之一。在 3D Humanoid 任务上测试了 ES 的扩展能力。

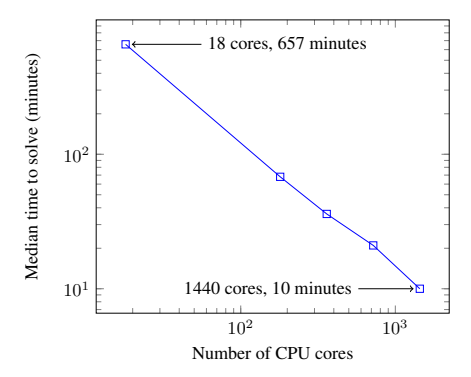
• 图 1：达到目标分数所需的时间随 CPU 核心数的变化。
• 结论：ES 展现了完美的线性加速。使用 1440 个核心，可以在 10 分钟 内解决 3D Humanoid 任务（单机通常需要 11 小时）。这证明了 ES 极低的通信开销使得大规模分布式训练成为可能。

4.4 对时间分辨率的不变性 (Invariance to Temporal Resolution)

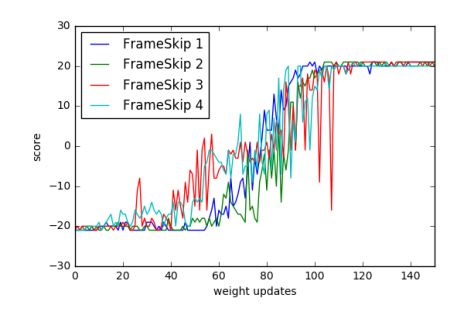
• 图 2：在 Pong 游戏中，改变 Frame-skip 参数（{1, 2, 3, 4}）。
• 结论：学习曲线几乎重合。这证明 ES 不像传统 RL 那样依赖精细调整的 Frame-skip 参数，具有更好的鲁棒性。

5. 结论 (Conclusion)

本文展示了进化策略 (ES) 是深度强化学习的一种强有力的竞争算法。

• 优势总结：
  1. 可扩展性：基于公共随机数的通信策略使得 ES 可以扩展到数千 CPU，实现线性加速。
  2. 简单性：无需反向传播，无需价值函数，代码实现简单。
  3. 鲁棒性：对稀疏奖励、长视界、动作频率不敏感。
• 展望：ES 特别适合元学习 (Meta-learning)、低精度硬件加速以及那些传统 MDP 方法难以处理的复杂奖励结构问题。