Evolving Connectivity for Recurrent Spiking Neural Networks

原文链接: http://arxiv.org/abs/2305.17650v1

作者: Guan Wang, Yuhao Sun, Sijie Cheng, Sen Song (清华大学)

摘要 (Abstract)

递归脉冲神经网络（RSNNs）因其受生物神经系统启发和建模复杂动力学的潜力，在通用人工智能（AGI）领域备受关注。然而，现有的基于代理梯度（Surrogate Gradient）的训练方法存在固有的不准确性，且对神经形态硬件不友好。

为了解决这些限制，作者提出了 演化连接性（Evolving Connectivity, EC） 框架。这是一个仅需推理（inference-only）的训练方法。EC 框架将权重调整重新表述为对参数化连接概率分布的搜索，并采用自然演化策略（Natural Evolution Strategies, NES）来优化这些分布。

主要特点： - 无需梯度：避免了梯度的计算。 - 硬件友好：具有稀疏的布尔连接（boolean connections）和高可扩展性。 - 高性能：在机器人运动控制任务中，性能媲美深度神经网络（DNN），优于梯度训练的 RSNN，甚至解决了复杂的 17-DoF 人形机器人任务。 - 高效率：比直接演化参数的方法快 2-3 倍。

1. 引言 (Introduction)

RSNNs 利用离散的脉冲信号进行信息传输，具有生物合理性和处理复杂时间动力学的能力。然而，训练 RSNNs 仍是一个挑战： - 代理梯度（Surrogate Gradients）的问题： - 算法上：梯度方向存在固有误差，且对函数尺度敏感。 - 实现上：与主流神经形态芯片（如 Loihi, SpiNNaker）不兼容，因为反向传播需要访问每个时间步的完整网络状态。

核心问题：能否设计一种无需梯度且不牺牲性能的 RSNN 训练方法？

受大脑连接概率分布和权重无关神经网络（WANN）的启发，作者提出了 EC 框架：将 RSNN 的架构重新构建为从参数化伯努利分布中独立采样的连接，并使用 NES 优化该概率分布。

2. 相关工作 (Related Works)

2.1 训练递归脉冲神经网络

• 生物可塑性规则 (STDP)：基础但难以处理复杂任务。
• 基于梯度的方法 (Surrogate Gradients)：目前性能最好，但难以在神经形态硬件上实现。
• E-prop：虽然针对硬件优化，但在性能上仍落后于代理梯度方法。 EC 的优势：从根本上通过“仅推理”框架解决了梯度有效性困境。

2.2 权重无关神经网络 (Weight-agnostic NNs)

WANN 和彩票票据假设（Lottery Ticket Hypothesis）表明，网络拓扑结构本身包含丰富信息，甚至随机权重的子网络也能表现优异。EC 进一步利用连接概率来参数化网络。

2.3 深度神经演化 (Deep Neuroevolution)

传统的演化策略（ES）主要优化连续的权重参数。EC 的创新在于搜索连接概率分布，这为硬件友好的 RSNN 演化提供了新思路。

3. 预备知识：递归脉冲神经网络 (Preliminaries: RSNN)

本文采用基于 Leaky Integrate-and-Fire (LIF) 神经元的 RSNN 模型，遵循 Dale's Law（区分兴奋性和抑制性神经元）。

神经元动力学方程： 膜电位 $\mathbf{u}$ 和突触电流 $\mathbf{c}$ 的变化如下：

$$ \tau_m \frac{\mathrm{d}\mathbf{u}^{(g)}}{\mathrm{d}t} = -\mathbf{u}^{(g)} + R\mathbf{c}^{(g)} \tag{1} $$

$$ \frac{\mathrm{d}\mathbf{c}^{(g)}}{\mathrm{d}t} = -\frac{\mathbf{c}^{(g)}}{\tau_{syn}} + \sum_{g_j} I_{g_j} \sum_{j} \mathbf{W}_{ij}^{(g_i g_j)} \delta(t - t_j^{s(g_j)}) + \mathbf{I}_{ext} \tag{2} $$

离散化形式（用于实际计算）：

$$ \mathbf{c}^{(t,g)} = d_c \mathbf{c}^{(t-1,g)} + \sum_{g_j} I_{g_j} \mathbf{W}^{(g_i g_j)} \mathbf{s}^{(t-1,g_j)} + \mathbf{I}_{ext}^{(t,g)} \tag{3} $$

$$ \mathbf{v}^{(t,g)} = d_v \mathbf{u}^{(t-1,g)} + R\mathbf{c}^{(t,g)} \tag{4} $$

$$ \mathbf{s}^{(t,g)} = \mathbf{v}^{(t,g)} > 1 \text{ (脉冲发放)} \tag{5} $$

$$ \mathbf{u}^{(t,g)} = \mathbf{v}^{(t,g)} (\mathbf{1} - \mathbf{s}^{(t,g)}) \text{ (复位)} \tag{6} $$

其中 $\mathbf{s}$ 是二值脉冲向量，$\mathbf{W}$ 是权重矩阵。

4. 框架 (Framework)

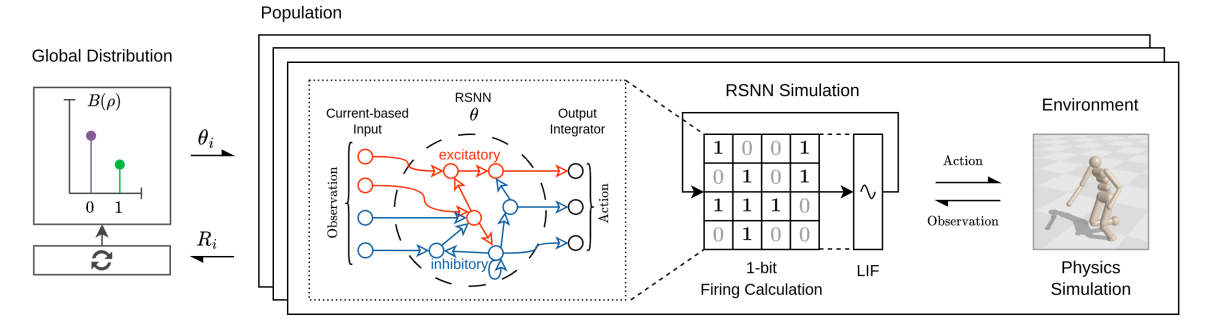
图 1: EC 架构示意图。种群的连接 $\theta^i$ 从全局分布 $B(\rho)$ 中采样并在并行环境中评估。

4.1 重构：从训练权重到训练连接概率 (Reformulation)

EC 框架的核心思想是放弃对浮点数权重值的训练，转而训练连接存在的概率。

传统神经网络中，突触连接通常表示为 $W_{ij} = w_{ij} \cdot \theta_{ij}$，其中 $w_{ij}$ 是连续的权重值，$\theta_{ij}$ 是二进制掩码（通常固定为 1）。而在 EC 框架中，我们做出了根本性的改变：

1. 同质化权重 (Homogeneous Weights)：我们将所有潜在连接的权重值 $w_{ij}$ 固定为单位大小（例如 1 或 -1，取决于突触是兴奋性还是抑制性）。这意味着我们不再学习连接的强度。
2. 概率化连接 (Probabilistic Connectivity)：我们引入一个连接概率矩阵 $\boldsymbol{\rho} = (\rho_{ij})$，其中每个元素 $\rho_{ij} \in [0, 1]$ 代表神经元 $i$ 和 $j$ 之间存在连接的概率。

在每次网络推理（前向传播）时，实际使用的连接矩阵 $\mathbf{W}$ 是通过对概率矩阵 $\boldsymbol{\rho}$ 进行伯努利采样得到的：

$$ \mathbf{W}_{ij} = \boldsymbol{\theta}_{ij}, \quad \text{其中} \quad \boldsymbol{\theta}_{ij} \sim B(\boldsymbol{\rho}_{ij}) = \begin{cases} 1 & \text{with probability } \rho_{ij} \\ 0 & \text{with probability } 1 - \rho_{ij} \end{cases} \tag{9} $$

直观理解： 这就好比对于神经网络中的每一个可能的突触连接，我们都有一枚不均匀的硬币。这枚硬币正面朝上的概率是 $\rho_{ij}$（我们要训练的参数）。 - 如果不幸抛到反面（$\theta_{ij}=0$），这个连接就断开了（权重为 0）。 - 如果抛到正面（$\theta_{ij}=1$），这个连接就建立了，且其强度直接被设定为固定的单位值（权重为 1）。

因此，训练的目标从“寻找最佳的权重值组合”转变为“寻找最佳的硬币概率分布”，使得采样出的网络结构（由 0 和 1 组成）能够最好地完成任务。

4.2 优化 (Optimization)

我们的目标是找到最优的概率分布 $\boldsymbol{\rho}$，使得从中采样出的网络 $\boldsymbol{\theta}$ 的期望性能 $R(\cdot)$ 最大化：

$$ \boldsymbol{\rho}^* = \arg\max_{\boldsymbol{\rho}} J(\boldsymbol{\rho}) = \arg\max_{\boldsymbol{\rho}} \mathbb{E}_{\boldsymbol{\theta} \sim B(\boldsymbol{\rho})}[R(\boldsymbol{\theta})] \tag{10} $$

由于伯努利采样过程不可导，我们无法使用传统的反向传播。作者采用了 自然演化策略 (Natural Evolution Strategies, NES) 来估计梯度。NES 的妙处在于它不需要对采样过程本身求导，而是通过评估多个采样样本的表现来估计分布参数的梯度：

$$ \nabla_{\boldsymbol{\rho}} J(\boldsymbol{\rho}) \approx \frac{1}{N} \sum_{i=1}^{N} \frac{\boldsymbol{\theta}_i - \boldsymbol{\rho}}{\boldsymbol{\rho} (1 - \boldsymbol{\rho})} R_i \tag{13} $$

这个公式告诉我们：如果某个采样样本 $\boldsymbol{\theta}_i$ 表现得好（$R_i$ 大），我们就调整 $\boldsymbol{\rho}$ 使得 $\boldsymbol{\theta}_i$ 出现的概率变大。

更新规则： $$ \boldsymbol{\rho}_{t} = \boldsymbol{\rho}_{t-1} + \frac{\eta}{N} \sum_{i=1}^{N} (\boldsymbol{\theta}_{i} - \boldsymbol{\rho}) R_{i} \tag{14} $$ 其中步长采用了自适应缩放。为了保持探索性，$\boldsymbol{\rho}$ 始终被限制在 $[\epsilon, 1-\epsilon]$ 区间内，防止概率完全变成 0 或 1 导致无法更新。

4.3 部署 (Deployment)

训练结束后，我们得到了一个优化好的概率矩阵 $\boldsymbol{\rho}$。在实际部署应用时，为了保证确定性，通常不再进行随机采样，而是使用阈值法： - 如果 $\rho_{ij} > 0.5$，则 $\mathbf{W}_{ij} = 1$。 - 如果 $\rho_{ij} \le 0.5$，则 $\mathbf{W}_{ij} = 0$。

这样就得到了一个固定的、稀疏的二进制（1-bit）权重矩阵用于推理。

5. EC 框架的特性 (Properties of EC Framework)

1. 仅推理 (Inference only)：无需反向传播，适用于不支持梯度的神经形态芯片（如 Loihi2, TrueNorth）。
2. 可扩展性 (Scalable)：评估过程相互独立，易于并行化。只需传输随机种子而非整个参数矩阵，通信开销极低。
3. 1-bit 连接 (1-bit connections)：使用整数运算代替浮点运算，节省内存并加速计算。

6. 实验 (Experiments)

6.1 实验设置

• 任务：机器人运动控制 (MuJoCo): Humanoid (17-DoF), Walker2d (6-DoF), Hopper (3-DoF)。
• 基线：
  • Deep RNNs: ES-LSTM, ES-GRU。
  • RSNNs: ES-RSNN (直接演化权重), SG-RSNN (代理梯度 + PPO)。

6.2 性能评估

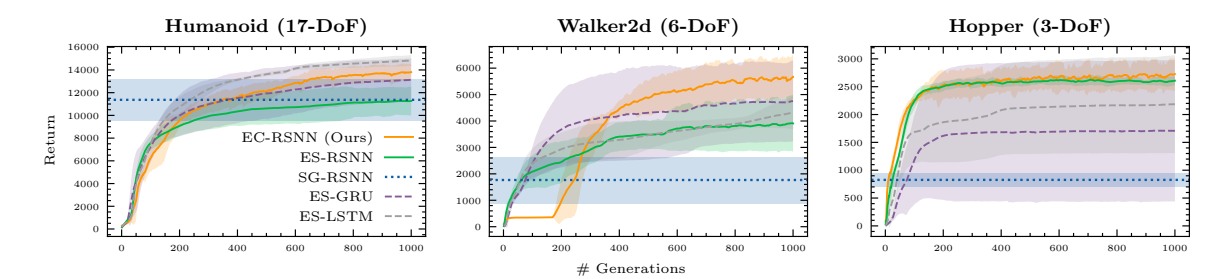
图 3: 性能对比。EC-RSNN（红线）在所有任务上均优于其他 RSNN 训练方法，并且在复杂的 Humanoid 任务上能与 Deep RNN 媲美。

• 对比 Deep RNNs：EC-RSNN 性能具有竞争力，甚至在 Walker2d 和 Hopper 上超过了 ES-GRU 和 ES-LSTM。
• 对比 RSNNs：
  • EC vs ES: EC 显著优于直接演化权重的 ES-RSNN。原因可能是 EC 在概率空间搜索具有更好的隐式并行性 (Schema Theory) 和更精细的优化能力。
  • EC vs SG: EC 优于代理梯度方法（SG-RSNN）。SG 方法对代理函数及其参数非常敏感（如图 4 所示），且梯度估计不准确。

6.3 效率对比

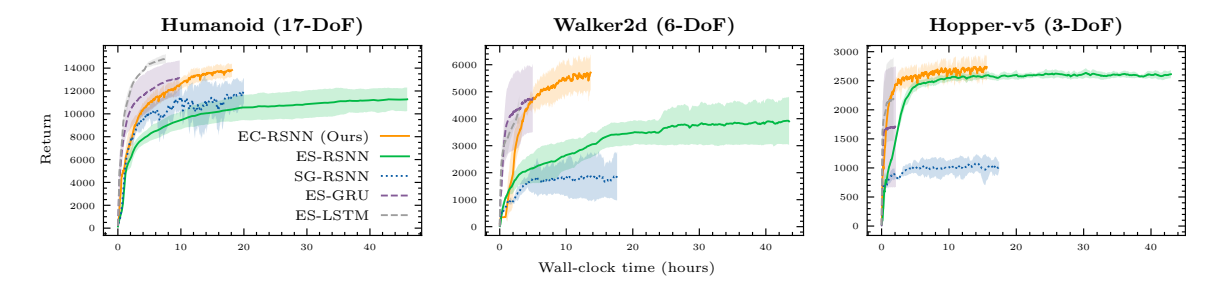
图 5: 效率对比。EC 在相同挂钟时间下收敛更快。

• 速度提升：由于使用了 1-bit 连接和整数运算，EC-RSNN 比浮点数运算的 ES-RSNN 快 2-3 倍。
• 收敛速度：EC 比需要反向传播的 SG 方法收敛更快。

7. 结论 (Conclusion)

EC 框架通过演化连接概率，提出了一种创新的、仅推理的 RSNN 训练方法。它不仅在性能上超越了传统的梯度方法，而且由于其 1-bit 连接特性，极大地降低了计算和内存成本，为神经形态硬件上的高效应用铺平了道路。

8. 局限性 (Limitations)

• 内存占用：演化算法需要存储 $N$ 个个体的参数，空间复杂度为 $O(N|\theta|)$。相比之下，梯度方法的时间复杂度依赖于时间步长。
• 权衡：演化方法更适合长序列任务（内存不随时间增长），梯度方法适合短序列任务。但 EC 通过存储 1-bit 数据减轻了这一开销。

9. 讨论 (Discussions)

• 神经形态硬件：EC 解决了片上学习（on-chip learning）的难题，支持云端大规模学习和边缘端的高效应用。
• 神经科学：
  • 提供了在复杂现实任务中研究 RSNN 的平台。
  • 提供了“神经元-神经元”级别的连接概率数据，这是目前实验技术难以获得的，有助于研究大脑连接组的基本原理（如模体、印迹等）。