A Hypercube-Based Encoding for Evolving Large-Scale Neural Networks (HyperNEAT) 论文笔记

作者: Kenneth O. Stanley, David B. D'Ambrosio, & Jason Gauci (University of Central Florida)
发表年份: 2009
核心贡献: 提出了一种名为 HyperNEAT 的方法，通过间接编码 (Indirect Encoding) —— 具体来说是 CPPN (Compositional Pattern-Producing Networks) —— 来生成大规模神经网络的连接权重。该方法利用了任务空间的几何特征 (Geometry)，能够生成具有数百万连接的、具有对称性和重复结构的网络，并且具备分辨率无关性 (Resolution Independence)。

1. 简介 (Introduction)

生物大脑拥有约 100 万亿个连接，其复杂性通过重复的模式（如皮层柱）和几何规律（如视网膜拓扑映射）来组织。然而，传统的人工神经网络进化（Neuroevolution, NE）方法产生的网络规模小且缺乏这种规律性。

1.1 传统方法的局限性：忽略几何信息

传统的 NE 方法（通常是直接编码，即基因直接对应连接）将神经网络视为输入和输出之间的黑盒映射。
* 问题: 这种视角丢弃了问题的几何结构。
* 例子: 如图 1 所示，对于一个机器人，传感器在物理空间上是相邻的，但在传统的全连接网络或直接编码中，输入 $I_1$ 和 $I_2$ 只是两个独立的节点，算法不知道它们在物理上是挨着的。打乱输入的顺序对算法来说没有区别，这意味着算法无法利用“相邻传感器可能包含相关信息”这一先验知识。

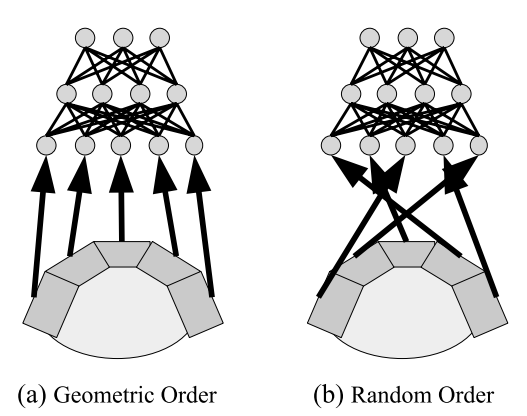
图 1: (a) 具有几何排列的输入。(b) 传统 ANN 将其视为无序集合。这导致算法必须独立学习每个连接，无法发现空间相关性。

HyperNEAT 的核心洞察: 通过利用问题的几何结构（Geometry），可以将学习任务从高维参数搜索转化为寻找低维的几何规律（Regularities）。

2. 背景 (Background)

HyperNEAT 建立在两个核心技术之上：CPPN 和 NEAT。

2.1 CPPN (Compositional Pattern-Producing Networks)

CPPN 是对生物发育过程的一种抽象。与生物通过化学物质扩散和细胞分裂进行发育不同，CPPN 通过函数的组合来生成空间模式。
* 原理: CPPN 是一个网络，其中的节点是数学函数（如高斯函数 Gaussian、正弦函数 Sine、Sigmoid、线性函数等）。
* 输入: 笛卡尔坐标（如 $x, y$）。
* 输出: 该坐标点的表现型属性（如灰度值、颜色等）。
* 特性:
* 对称性: 通过高斯函数 $f(x) = e^{-x^2}$ 等对称函数获得。
* 重复性: 通过周期函数 $\sin(x)$ 获得。
* 重复并变异: 周期函数与线性函数的组合。

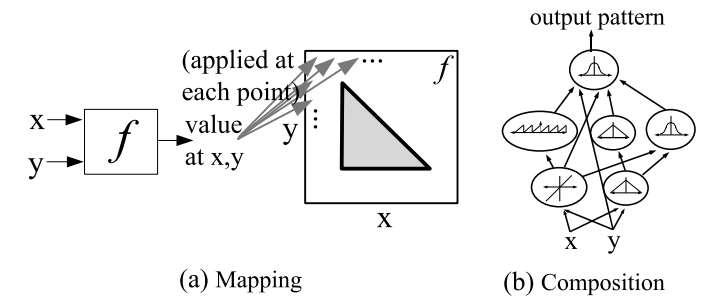
图 2: (a) 函数 $f$ 决定了二维空间中的图案。(b) CPPN 网络的结构决定了函数的组合方式。

2.2 NEAT (NeuroEvolution of Augmenting Topologies)

NEAT 是一种进化神经网络拓扑和权重的方法（参见 NEAT 论文笔记）。在 HyperNEAT 中，NEAT 被用来进化 CPPN。
* NEAT 从简单的结构开始，通过突变逐渐增加 CPPN 的复杂度（添加新的函数节点或连接）。
* 这使得 HyperNEAT 能够随着进化的进行，发现越来越复杂的几何规律。

3. HyperNEAT 方法论 (Methodology)

HyperNEAT 的核心在于如何将 CPPN 生成的空间模式映射为神经网络的连接（Connectivity）。

3.1 核心映射机制：超立方体中的连接 (Hypercube-Based Geometric Connectivity)

HyperNEAT 不再像标准 CPPN 那样输入一个点的坐标 $(x, y)$ 输出该点的强度，而是输入两个点的坐标，输出它们之间连接的权重。

假设我们要在二维平面上构建一个神经网络，该平面被称为底板 (Substrate)。
* 输入: 两个节点的坐标，源节点 $(x_1, y_1)$ 和目标节点 $(x_2, y_2)$。这构成了 4 维超空间 $(x_1, y_1, x_2, y_2)$。
* 处理: CPPN 作为一个 4 维函数 $CPPN(x_1, y_1, x_2, y_2)$ 进行计算。
* 输出: 连接权重 $w$。

数学表达

$$ w_{ij} = CPPN(x_i, y_i, x_j, y_j) $$
其中 $(x_i, y_i)$ 是神经元 $i$ 的物理位置，$(x_j, y_j)$ 是神经元 $j$ 的物理位置。

具体执行步骤

1. 定义底板 (Substrate): 确定神经元在二维（或三维）空间中的布局。例如，一个 $5 \times 5$ 的网格，坐标范围从 -1 到 1。
2. 查询 (Querying): 遍历底板中每一对可能的连接 $(i, j)$。
3. 计算权重: 将坐标传入 CPPN 计算输出。
4. 阈值处理与缩放:
   • 如果 $|CPPN_{out}| < w_{min}$ (最小阈值)，则该连接不存在（权重为 0）。
   • 否则，将输出缩放到特定范围（如 $[-3, 3]$）作为权重。

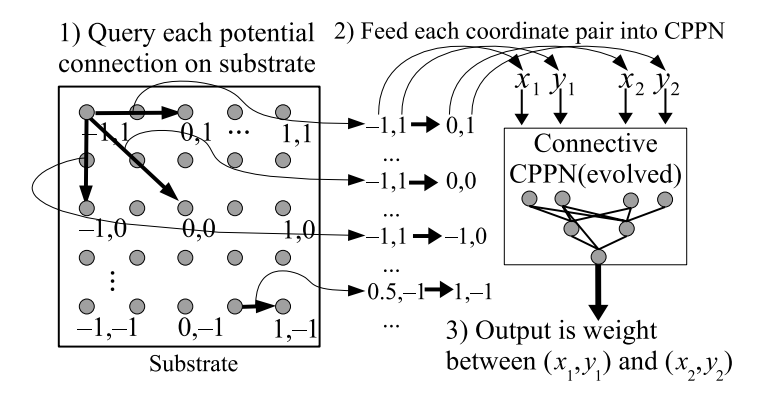
图 4: 映射过程示意图。
1. Substrate: 定义了节点的几何位置。
2. CPPN Query: 对于底板上的任意两个节点（源和目标），将其坐标 $(x_1, y_1, x_2, y_2)$ 输入 CPPN。
3. Connection Weight: CPPN 的输出决定了这两个节点间的连接权重。
最终结果是：CPPN 定义了一个 4 维超立方体中的模式，这个模式被“切片”并投影回低维空间，形成了神经网络的连接矩阵。

3.2 几何规律的具体例子 (Conceptual Examples)

通过 CPPN 的函数组合，可以轻松产生具有特定几何特征的连接模式：

• 对称性 (Symmetry):
  • 如果 CPPN 包含函数 $w = \text{Gaussian}(x_1)$，那么对于所有 $x_1$ 相同的源节点（不管 $y_1, x_2, y_2$ 如何），它们发出的连接权重分布将关于 $x_1=0$ 对称。这可以产生左右对称的连接结构。
• 局部性 (Locality):
  • 如果 CPPN 计算的是 $w = \text{Gaussian}(x_1 - x_2) \cdot \text{Gaussian}(y_1 - y_2)$，那么只有当 $(x_1, y_1)$ 和 $(x_2, y_2)$ 非常接近时，权重 $w$ 才会很大。这自然地编码了“每个神经元只连接其邻居”这一概念（类似卷积核或感受野）。
• 重复性 (Repetition):
  • 如果使用周期函数 $\sin(x_1)$，连接模式会在空间中重复出现。

3.3 输入/输出配置 (Substrate Configuration)

HyperNEAT 允许根据任务的物理性质自由配置底板。
* Grid (网格): 适用于图像处理。
* Sandwich (三明治结构): 输入层和输出层分层排列，中间无连接或全连接。
* Circular (环形): 适用于圆形机器人的传感器布局。

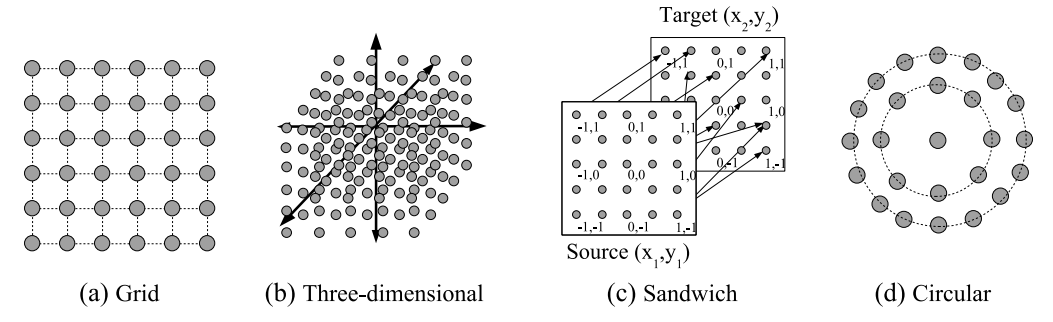
图 6: 不同的底板配置。(a) 网格 (b) 3D 立方体 (c) 三明治结构 (d) 环形结构。

3.4 分辨率无关性 (Resolution Independence)

这是 HyperNEAT 最强大的特性之一。
* 概念: CPPN 编码的是连接的模式 (Pattern) 或概念 (Concept)，而不是具体的连接列表。它是一个连续函数。
* 缩放: 我们可以在训练时使用 $11 \times 11$ 的低分辨率底板。训练完成后，直接在一个 $33 \times 33$ 的高分辨率底板上重新查询同一个 CPPN。
* 结果: 能够平滑地生成更密集的网络，通常无需重新训练即可保留原有功能（类似于矢量图放大）。这使得演化百万级连接的网络成为可能。

4. 实验 1: 视觉辨别 (Visual Discrimination)

4.1 任务设置

• 目标: 在视野中找到最大的物体（两个黑色方块，一大一小）的中心。
• 底板: "三明治"结构。输入层是视网膜，输出层是目标图（Target field）。
• 挑战: 必须发现“累积邻域激活”的几何规律，并将其应用到视野的每一个角落（平移不变性）。

4.2 对比实验

• HyperNEAT: 进化 CPPN。
• PNEAT (Perceptron NEAT): 直接编码的 NEAT，直接进化连接权重。
• 分辨率: 训练时 $11 \times 11$ (14,641 个潜在连接)。

4.3 结果

1. 泛化能力: HyperNEAT 显著优于 PNEAT。PNEAT 必须独立学习每个位置的权重，难以泛化到未见过的物体位置；HyperNEAT 学会了“几何规则”，天然具备泛化能力。
2. 缩放能力: 将训练好的 CPPN 应用于 $33 \times 33$ 甚至 $55 \times 55$ 的底板：
   • 连接数从 1.4 万增加到 800 万以上。
   • 性能几乎没有下降。这是直接编码方法完全无法做到的。

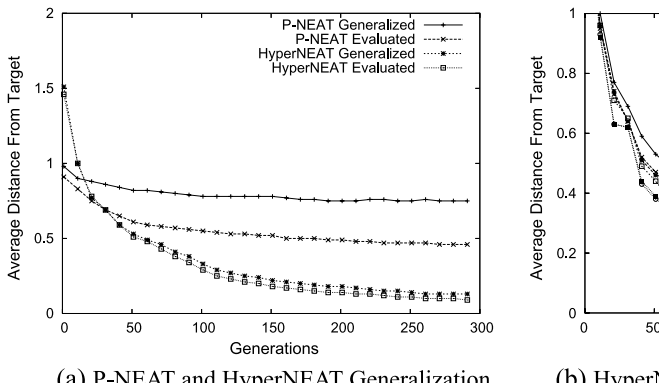
图 10 (a): HyperNEAT 在泛化测试中表现优异，而 PNEAT 表现较差。

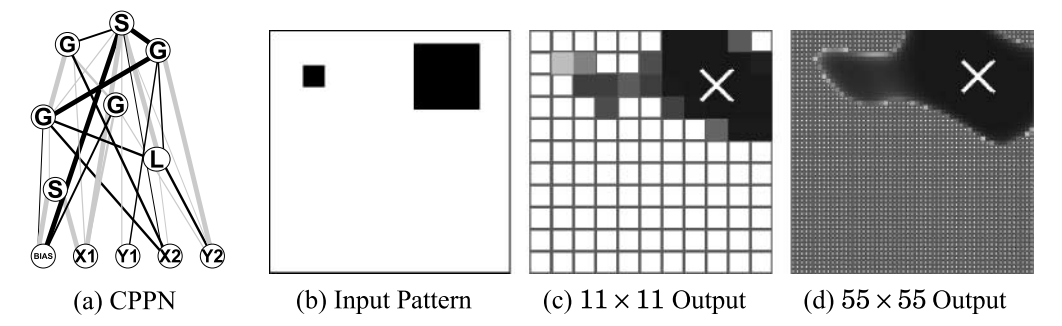
图 11: 同一个 CPPN 在 (c) $11 \times 11$ 和 (d) $55 \times 55$ 分辨率下产生的激活模式。注意高分辨率下的平滑性和功能的保持。

5. 实验 2: 食物收集 (Food Gathering)与几何偏置

5.1 任务设置

• 目标: 机器人去吃食物。
• 传感器: 环绕机器人的距离传感器。
• 几何布局: 测试两种底板布局，以验证几何结构的重要性。
  1. Concentric (同心圆): 传感器在内圈，执行器在外圈，角度对应。符合机器人实际物理形状。
  2. Parallel (平行线): 传感器和执行器展开成两条平行线。

5.2 几何偏置 (Geometric Bias)

为了帮助 CPPN 更容易发现局部性规律，可以引入额外的输入：
$$ CPPN(x_1, y_1, x_2, y_2, \Delta) $$
其中 $\Delta$ 是两点间的距离（Length）。这是一种人为注入的领域知识（Inductive Bias）。

5.3 结果

1. 布局影响: Parallel 布局比 Concentric 更容易学习（收敛更快）。因为在笛卡尔坐标系下，平行线的“对齐”关系比圆形的“角度”关系更容易用简单的线性/周期函数表达。
2. 几何偏置的作用: 加入 $\Delta$ (距离) 输入后，两种布局的表现差异消失了，且都变好了。这说明显式的几何信息能显著简化搜索难度。
3. 不完美的缩放: 与视觉任务不同，食物收集任务在缩放时性能有所下降（Artifacts）。因为高分辨率引入了新的细节（更窄的传感器视角），这些是在低分辨率下从未见过的。但即便如此，经过极短的再进化（几代），性能就能恢复并超越。

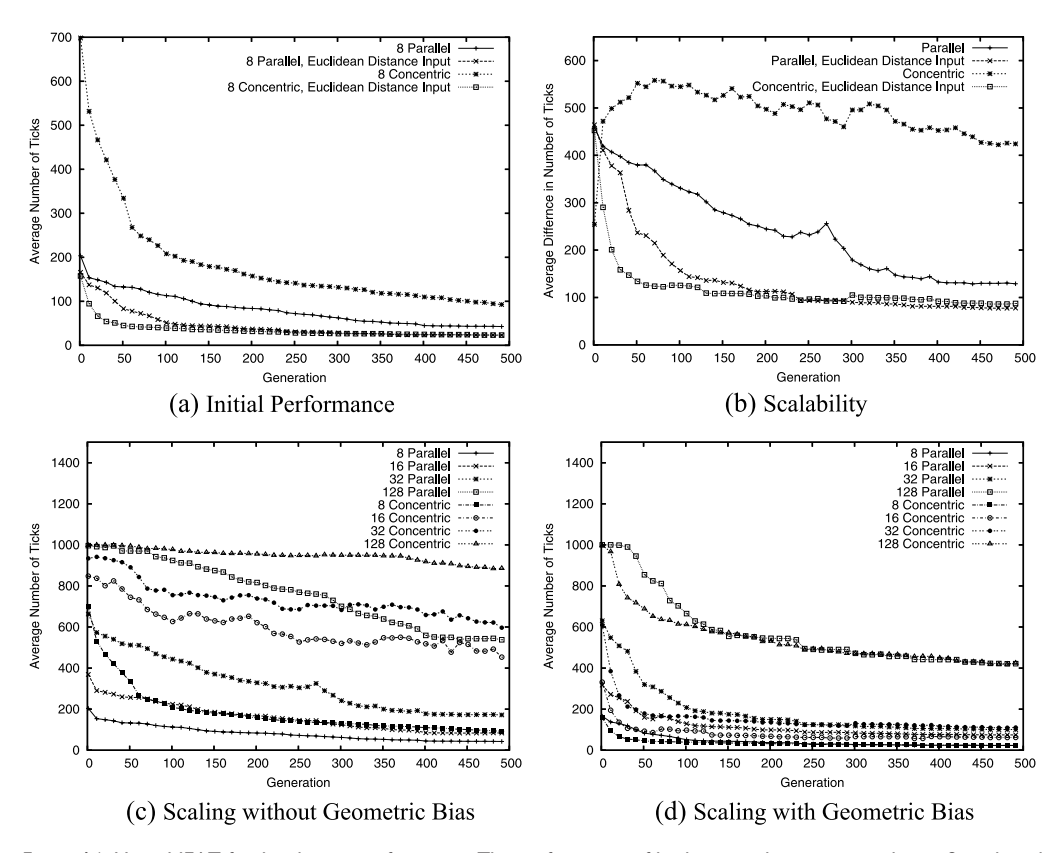
图 14: (a) 平行布局 (Parallel) 比同心布局 (Concentric) 学得快，但加入距离输入 (w/ dist) 后两者都变快且持平。

6. 讨论与总结 (Discussion & Conclusion)

6.1 为什么直接编码行不通？

对于大规模网络（如 14,000+ 连接），搜索空间维度过高（Curse of Dimensionality）。PNEAT 失败证明了这一点。HyperNEAT 搜索的是生成权重的规则（CPPN 复杂度极低，可能只有几十个节点），而不是权重本身，因此极大地压缩了搜索空间。

6.2 几何即信息

HyperNEAT 的核心哲学是：问题的结构（Structure）比维度（Dimensionality）更重要。
* 如果问题具有几何规律（如图像、物理空间），HyperNEAT 可以利用这些规律来构建极其庞大的网络。
* 通过合理设计底板（Substrate），我们可以将人类对任务几何结构的理解注入到进化过程中。

6.3 缩放的意义

HyperNEAT 首次展示了在低分辨率下学习，然后零成本迁移到高分辨率（百万级连接）的能力。这为进化极大规模神经网络提供了一条可行的路径：
1. 在低分辨率下快速进化出核心概念。
2. 扩展分辨率。
3. （可选）在高分辨率下进行微调。

一句话总结: HyperNEAT 通过进化一个 4 维空间函数 (CPPN) 来生成神经网络的权重矩阵，从而巧妙地利用了几何规律，实现了神经网络的无限分辨率缩放和百万级连接的进化。