Brain-inspired global-local learning incorporated with neuromorphic computing

来源: Nature Communications (2022)

链接: https://www.nature.com/articles/s41467-021-27653-2

Code Availability: https://github.com/yjwu17/Spiking-hybrid-plasticity-model

Abstract

人工智能的学习主要有两种途径：误差驱动的全局学习（error-driven global learning）和面向神经科学的局部学习（neuroscience-oriented local learning）。将两者结合到一个网络中可能为通用学习场景提供互补的学习能力。本文提出了一种类脑神经形态全局-局部协同学习模型（neuromorphic global-local synergic learning model）。该模型引入了类脑元学习范式（brain-inspired meta-learning paradigm）和包含神经动力学及突触可塑性的可微分脉冲模型。它能够元学习（meta-learn）局部可塑性，并接收自顶向下的监督信息进行多尺度学习。该模型在少样本学习（few-shot learning）、持续学习（continual learning）和神经形态视觉传感器的容错学习（fault-tolerance learning）等任务中表现出显著优势。此外，通过算法-硬件协同设计，该模型在天机（Tianjic）神经形态平台上得到了实现，证明了其能充分利用众核架构发展混合计算范式。

Introduction

大多数神经形态模型建立在单一的反向传播（Backpropagation, BP）或单一的局部可塑性（Local Plasticity, LP）之上。
* 全局学习 (BP): 全局误差驱动，层层分配监督误差。在图像分类和强化学习中表现良好，但缺乏生物合理性。
* 局部学习 (LP): 本质上是相关性驱动（correlation-driven），发生在突触前后神经元之间，由异步脉冲活动触发。具有低延迟和高能效的优势，但在复杂任务上性能通常不如 SOTA。

为了结合两者优势，本文提出了一种混合学习模型。相关研究包括三因素学习规则（three-factor learning rule）和元学习（meta-learning）。本文的方法通过元学习范式和微分脉冲动力学模型，实现了LP和GP的通用灵活集成，并支持在神经形态芯片上的高效混合学习。

Results

Hybrid synergic learning model

该模型利用了神经科学关于突触调节行为和多尺度学习机制的线索（图 1a）。
1. 多尺度元学习: 神经调节剂（Neuromodulators）作为元学习参数 $\theta$ 作用于突触可塑性。LP的超参数（如学习率、滑动阈值）被公式化为元参数 $\theta$。
2. 双层优化 (Bilevel Optimization): 将权重 $w$ 和元参数 $\theta$ 的学习过程解耦。$w$ 通过全局误差更新，$\theta$ 通过元学习更新（图 1b）。
3. 参数化建模: 将局部突触增量 $\Delta w_{LP}$ 建模为关于突触前/后脉冲活动和局部超参数 $\theta$ 的参数化函数（图 1c）。
4. 权重分解: 突触权重 $w(t)$ 被分解为两部分：$w_{GP}$（由BP更新）和 $w_{LP}$（由元学习的脉冲LP更新）（图 1d）。

$$w(t) = w_{GP} + w_{LP}$$

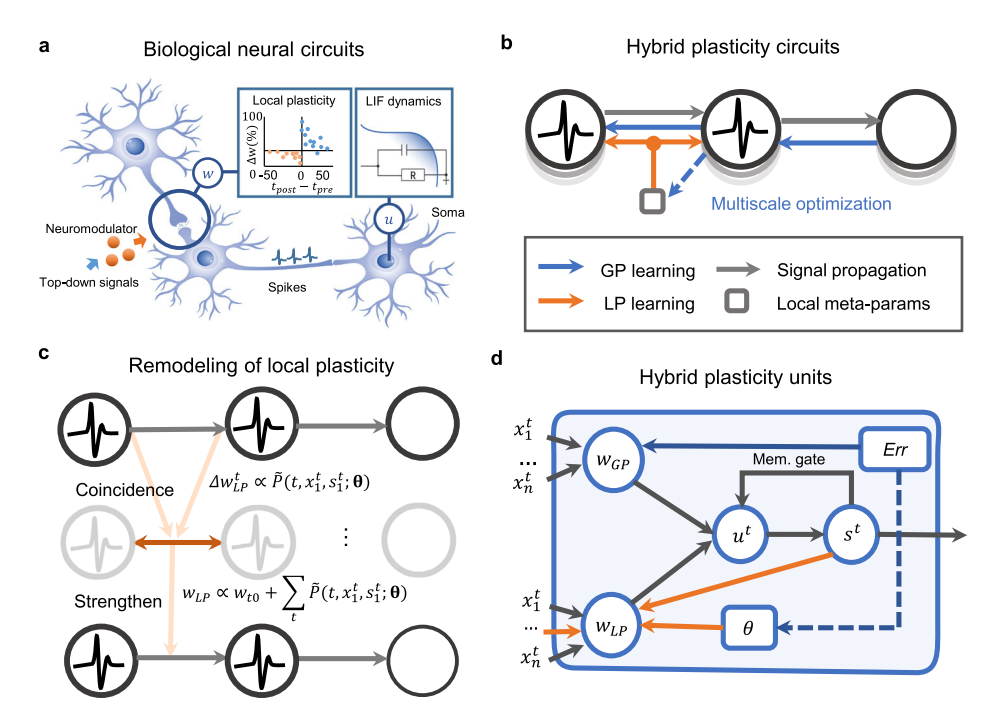
图 1: 混合协同学习模型示意图。(a) 生物突触可塑性与神经动力学。(b) 多尺度元学习范式。(c) 参数化生物短时程可塑性。(d) 混合可塑性 (HP) 单元结构。

Baseline performance evaluation

在 MNIST, Fashion-MNIST, CIFAR10, CIFAR10-DVS, DVS-Gesture 等数据集上进行了评估（Table 1）。
* 图像分类: HP SNN 相比其他脉冲模型取得了更高的准确率。
* 编码方式: 支持频率编码（rate coding）和时间排序编码（temporal rank order coding）。排序编码延迟更低，频率编码在长窗口下准确率更高（图 2）。
* 收敛性: 相比单一 LP、单一 GP 和微调（fine-tuning）方法，HP 模型收敛更快且准确率更高（图 3）。

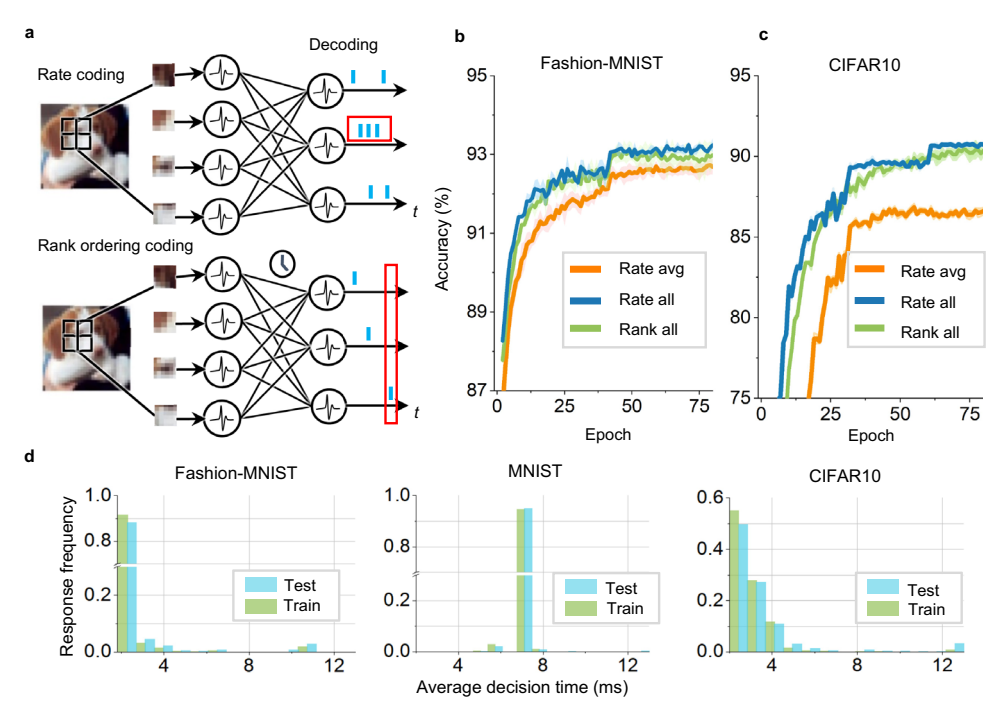
图 2: 支持不同的编码方案。(a) 频率编码与时间排序编码。(b, c) 不同编码下的训练曲线。(d) 平均响应时间。

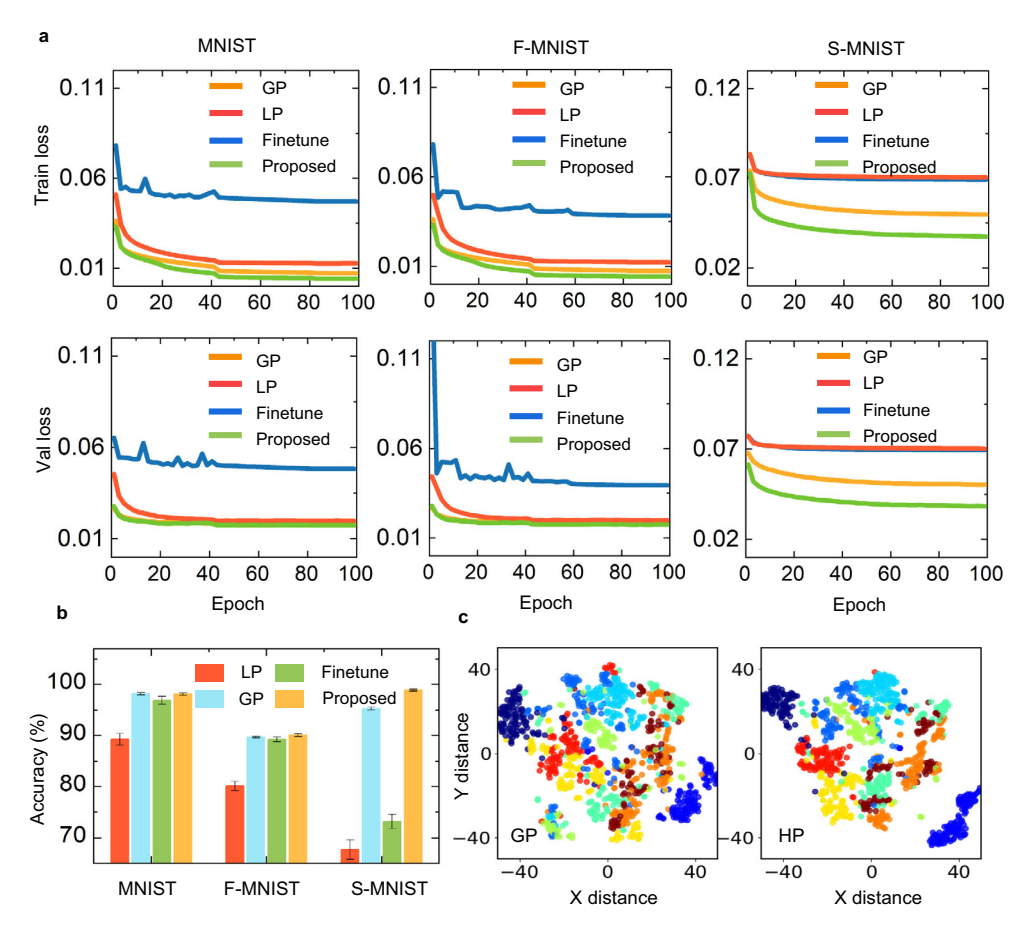
图 3: 收敛性对比。(a) 收敛曲线。(b) 准确率直方图。(c) 隐层激活的 t-SNE 可视化。

Fault-tolerance learning

神经形态视觉传感器（NVS）常受噪声和背景干扰影响。利用基于 Hebbian 的局部模块，HP 模型提高了容错能力。
* 实验: 使用裁剪（cropping）和噪声混合（noise-mixed）的数据测试。
* 结果: 随着裁剪区域或噪声增加，HP 模型表现出更强的鲁棒性（图 4c, d）。
* 分析: HP 模型减小了不完整模式与原始模式在隐层激活上的距离（欧氏距离和余弦相似度），表明局部模块有助于利用先前的关联特征（图 4e, f）。

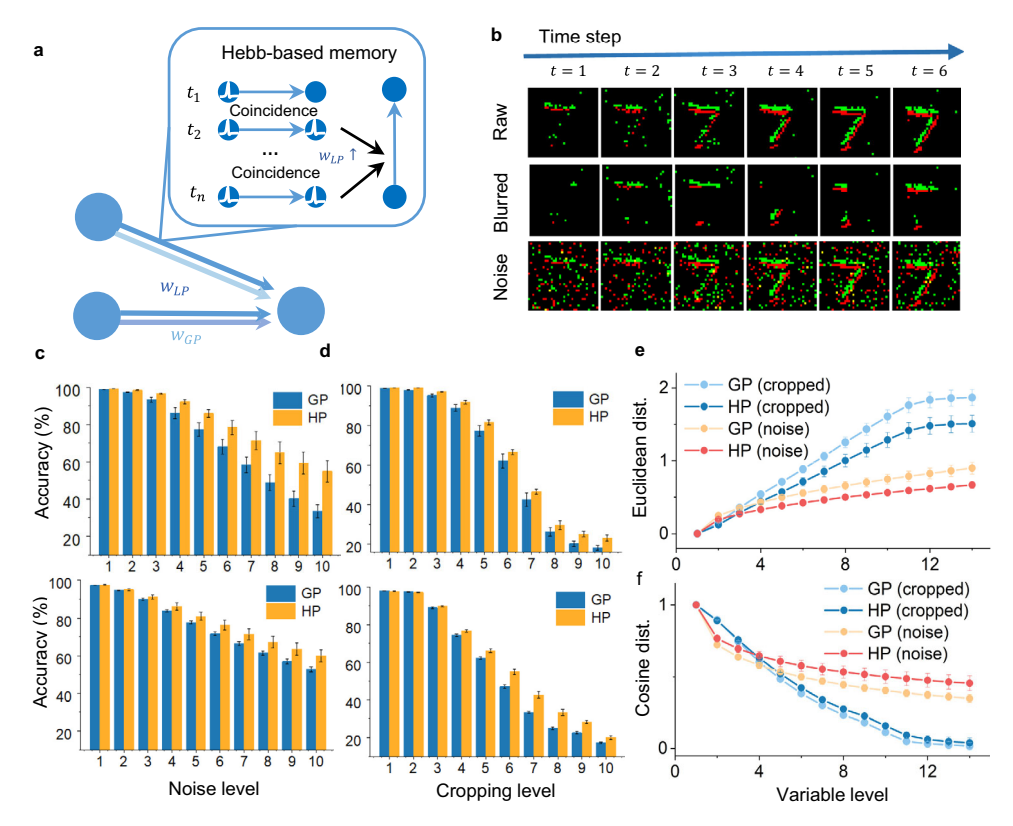
图 4: 混合可塑性提高容错能力。(a) 相关性局部模块的记忆功能。(b) 不完整数据的生成。(c, d) 裁剪和噪声实验的性能对比。(e, f) 隐层激活的距离分析。

Few-shot learning

利用 Omniglot 数据集评估少样本学习能力。
* 机制: GP 模块提取判别性特征，LP 模块从有限样本对中发现归纳偏置（inductive bias）。
* 性能: 5-way 1-shot 达到 98.7%，20-way 1-shot 达到 94.6%，显著优于单一 GP 模型和之前的 SNN，与非脉冲 SOTA 结果相当（图 5a, b, Table 2）。

Continual learning

在乱序 MNIST (Shuffled MNIST) 上进行 50 个任务的持续学习。
* 策略: 稀疏重叠连接用于 GP 学习特定任务信息，LP 学习任务间的通用特征。
* 结果: HP 模型在 50 个任务后保持了最佳性能，优于稀疏 GP 和 XdG 方法（图 5c）。

Effectiveness analyses

• 隐式损失 (Implicit Loss): 将局部权重更新视为隐式损失函数的导数。LP 学习类似于优化 Hopfield 网络或异联想记忆（HAM）的能量函数，作为一种正则化，强化了触发神经元并发放电的权重。
• 度量学习 (Metric Learning): 在少样本学习中，局部模块将输入模式投影到余弦嵌入空间，通过拉近类内距离、推远类间距离来加速收敛。

Hybrid computation on the Tianjic

将模型部署在天机神经形态芯片上，利用算法-硬件协同设计。
* 效率: 支持多种编码，能耗随网络规模增加极其缓慢。
* 吞吐量与通信: 混合学习方案灵活分配 GP 和 LP。仅少量连接需要全局监督信号，显著减少了核间通信负载，利用众核架构实现高吞吐量（图 5e, f）。

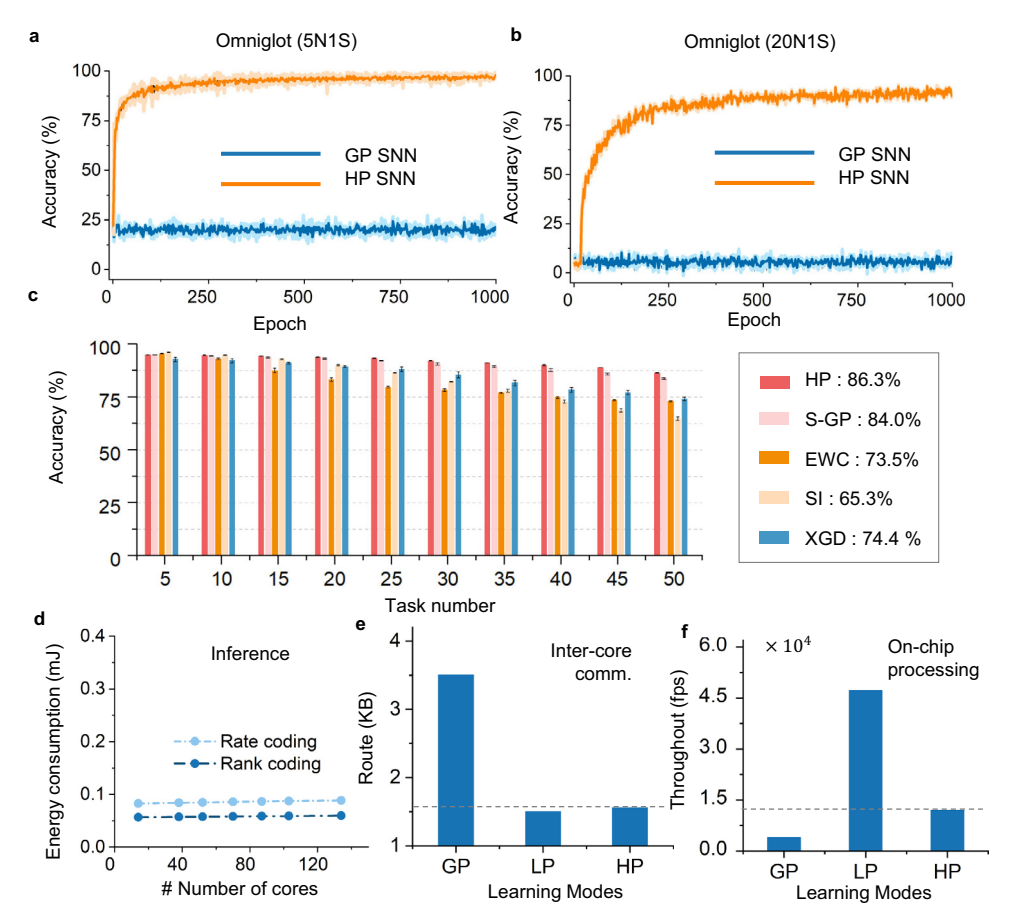
图 5: 性能评估。(a, b) Omniglot 少样本学习曲线。(c) Shuffled MNIST 持续学习准确率。(d) 天机芯片上的能耗评估。(e) 核间通信资源对比。(f) 片上学习吞吐量评估。

Discussion

本文提出的混合模型通过元学习范式集成了全局和局部学习，不仅在标准分类任务上表现优异，还在少样本、持续学习和容错学习等复杂场景中展现出优势。通过在天机芯片上的实现，证明了该模型在神经形态硬件上的高效性和算法-硬件协同设计的潜力。

Methods

Model establishment

1. 膜电位动力学:
   $$\tau_u \frac{du_i}{dt} = -u_i(t) + \sum_{j=1}^{l_n} w_{ij}(t) s_j(t)$$
2. 离子通道/权重动力学:
   $$\tau_{w} \frac{dw_{ij}}{dt} = w_{ij}^{g} - w_{ij}(t) + P(t, pre_{j}(t), post_{i}(t); \theta)$$
   其中 $P$ 是通用的局部可塑性项。
3. 参数化 Hebbian 规则:
   $$P \triangleq k^{corr} s_i(t) (\rho(u_i(t)) + \beta_i)$$
   包含局部学习率、非线性函数 $\rho$ 和滑动阈值 $\beta_i$ 等超参数 $\theta$。
4. 信号传播方程 (离散化):
   结合上述方程，使用改进的欧拉法得到迭代公式（Eq. 10），将权重分为两部分：
   $$u_i^l(t_m) \approx \dots + k_u \sum_{j} (w_{ij}^l(t_m) e^{\dots} + \alpha_i^l P_{ij}^l(t_m)) s_j^{l-1}(t_m)$$
   其中 $\alpha^l$ 控制局部模块的影响。

Optimization

采用双层优化（Bilevel Optimization）策略：
* 下层: 使用 BPTT 更新权重 $\mathbf{w}$。
$$\mathbf{w}^*(\boldsymbol{\theta}) = \arg \min_{\mathbf{w}} C_{\pi_i}^{train}(\mathbf{w}^*, \boldsymbol{\theta})$$
* 上层: 在验证集上更新元参数 $\boldsymbol{\theta}$（包括 $\alpha, \eta, \beta$ 等）。
$$\nabla_{\boldsymbol{\theta}_{k}} \tilde{\mathbf{C}} \approx \sum_{\pi_{i} \in \Gamma_{s}} \nabla_{\boldsymbol{\theta}} C_{\pi_{i}}^{val}(\mathbf{w}_{k} - \xi \nabla_{\mathbf{w}} C_{\pi_{i}}^{train}(\mathbf{w}_{k-1}, \boldsymbol{\theta}_{k-1}), \, \boldsymbol{\theta}_{k})$$

Implicit loss function

总损失函数 $E$ 可以分解为显式分类损失 $C$ 和由网络动力学产生的隐式损失 $E_{in}$：
$$E \triangleq C + \lambda_3 E_{in}$$
对于容错学习，局部权重增量 $\Delta w$ 可视为 $E_{in}$ 的导数，推导出 $E_{in}$ 类似于 HAM 的能量函数：
$$E_{in} \approx -\sum_{t} \sum_{l} \mathbf{s}_t^{l-1} \mathbf{w}_t^l \mathbf{s}_t^l$$
这意味着局部学习倾向于加强那些能触发并发放电的连接，形成能量景观中的局部极小值。

Metric learning analysis

在少样本学习中，局部模块构建了一个 Hebbian 矩阵：
$$\mathbf{w}_{LP} = \sum_{k} \mathbf{y}_k \mathbf{c}_k^T$$
其中 $\mathbf{c}_k$ 是类别的特征中心。对于查询样本 $\tilde{\mathbf{x}}$，局部模块产生归纳偏置 $I_{LP} \propto \mathbf{c}_k^T \tilde{\mathbf{x}}$（余弦相似度）。这迫使网络在度量空间中学习，使得类内距离小、类间距离大。

Availability

• 数据: MNIST, N-MNIST, Omniglot 公开可用。
• 代码: https://github.com/yjwu17/Spiking-hybrid-plasticity-model