Discovering Reinforcement Learning Algorithms

作者/机构: DeepMind

日期: 2021-01

原文链接: https://arxiv.org/abs/2007.08794

1. 摘要与核心贡献

强化学习 (RL) 算法通常依赖于人工设计的更新规则（如 TD-learning, Policy Gradient）。本文提出了 Learned Policy Gradient (LPG)，一种通过元学习 (Meta-learning) 从数据中自动发现的强化学习算法。

LPG 的核心突破在于：
* 端到端发现更新规则：不预设“价值函数”等概念，而是让算法自己发现“预测什么”（What to predict）以及“如何利用预测进行学习”（How to learn from it）。
* 通用性：虽然仅在简单的玩具环境（Toy Environments）中进行元训练，LPG 能够泛化到复杂的 Atari 游戏中，并取得非凡的性能。
* 自发现的引导机制 (Bootstrapping)：LPG 自动发现了类似价值函数的语义，并学会了利用这些预测进行引导（Bootstrapping）。

2. 方法 (Method)

LPG 将寻找最优 RL 算法的问题转化为一个元学习问题。目标是找到一个参数化的更新规则 $\eta$，使得使用该规则更新的 Agent 在各种环境分布 $p(\mathcal{E})$ 下能获得最大的累积回报。

2.1 总体架构

LPG 的架构包含两个主要部分：
1. Agent ($\theta$)：在环境中交互，产生策略 $\pi_\theta(a|s)$ 和预测向量 $y_\theta(s)$。
2. LPG Update Rule ($\eta$)：这是一个元学习到的 LSTM 网络，它观察 Agent 的轨迹，并输出如何更新 Agent 的参数。

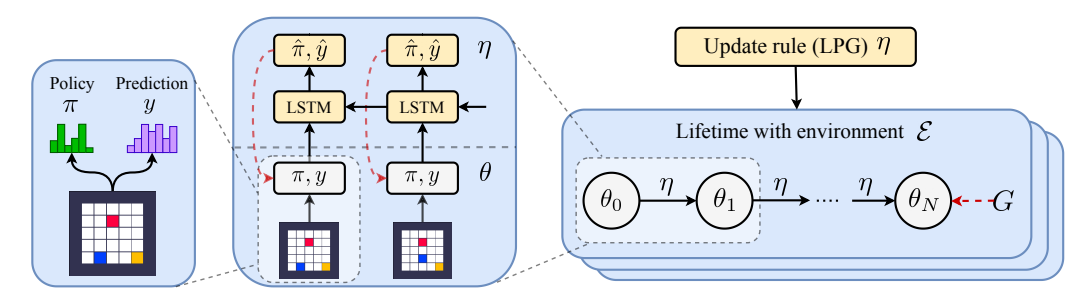
图 1: LPG 元训练流程。(左) Agent 产生策略 $\pi$ 和预测向量 $y$。(中) LPG ($\eta$) 接收 Agent 的输出作为输入，通过反向 LSTM (Backward LSTM) 生成更新目标 $\hat{\pi}$ 和 $\hat{y}$。(右) 在多个并行环境中元训练 $\eta$。

2.2 LPG 架构细节

LPG 是一个由 $\eta$ 参数化的反向 LSTM 网络。在每个时间步 $t$，它接收以下输入：
$$ x_t = [r_t, d_t, \gamma, \pi(a_t|s_t), y_{\theta}(s_t), y_{\theta}(s_{t+1})] $$
其中：
* $r_t$: 奖励
* $d_t$: 终止信号
* $\gamma$: 折扣因子
* $\pi(a_t|s_t)$: 当前动作的概率
* $y_\theta(s)$: Agent 对当前状态的预测向量（$m$ 维，$y \in [0, 1]^m$）

LPG 输出两个更新目标：
1. $\hat{\pi} \in \mathbb{R}$: 策略调整方向。
2. $\hat{y} \in [0, 1]^m$: 预测向量的目标值。

注意：LPG 不接收原始观测 $s_t$ 或动作 $a_t$ 作为输入，这使得它与环境的观测空间和动作空间解耦，从而具备跨环境泛化的能力。

2.3 Agent 更新规则 (The Inner Loop)

Agent 的参数 $\theta$ 通过梯度上升进行更新。LPG 输出的 $\hat{\pi}$ 和 $\hat{y}$ 定义了更新的方向：

$$ \Delta \theta \propto \mathbb{E}_{\pi_{\theta}} \left[ \underbrace{\nabla_{\theta} \log \pi_{\theta}(a|s) \hat{\pi}}_{\text{Policy Update}} - \alpha_{y} \underbrace{\nabla_{\theta} D_{\text{KL}}(y_{\theta}(s) \| \hat{y})}_{\text{Prediction Update}} \right] \tag{2} $$

• 策略更新: $\hat{\pi}$ 直接调节动作概率。如果 $\hat{\pi} > 0$，则增加当前动作的概率；反之则减少。这类似于 Policy Gradient 中的优势函数 $A(s, a)$。
• 预测更新: Agent 的预测向量 $y_\theta(s)$ 被训练去逼近 LPG 输出的目标 $\hat{y}$（通过最小化 KL 散度）。
  • 关键点: $y_\theta$ 最初没有预定义的语义（不是 Value Function）。LPG 必须自己学会在 $\hat{y}$ 中编码有用的信息（如未来奖励），并通过 $\hat{\pi}$ 利用这些信息来改进策略。

2.4 LPG 更新规则 (The Outer Loop)

LPG 的参数 $\eta$ 通过元梯度（Meta-gradient）进行更新，目标是最大化 Agent 在生命周期结束时的预期回报 $G$：

$$ \eta^* = \arg\max_{\eta} \mathbb{E}_{\mathcal{E} \sim p(\mathcal{E})} \mathbb{E}_{\theta_0 \sim p(\theta_0)} [G] \tag{1} $$

实际的元梯度更新包含正则化项，以稳定极其困难的优化过程：

$$ \Delta \eta \propto \mathbb{E}_{\mathcal{E}} \mathbb{E}_{\theta_0} \left[ \nabla_{\eta} \log \pi_{\theta_N}(a|s) G + \text{Regularizers} \right] \tag{4} $$

正则化项 (Regularizers):
$$ \beta_0\nabla_{\eta}\mathcal{H}(\pi_{\theta_N}) + \beta_1\nabla_{\eta}\mathcal{H}(y_{\theta_N}) - \beta_2\nabla_{\eta}\|\hat{\pi}\|_2^2 - \beta_3\nabla_{\eta}\|\hat{y}\|_2^2 $$
* 熵正则化 ($\mathcal{H}(\pi), \mathcal{H}(y)$): 鼓励策略和预测保持一定的随机性，防止过早收敛到确定性行为。
* L2 正则化 ($\|\hat{\pi}\|, \|\hat{y}\|$): 防止更新步长过大。

2.5 自动超参数平衡 (Hyperparameter Balancing)

由于不同环境适合的学习率 ($\alpha$) 不同，固定超参数会导致元训练不稳定。论文提出联合优化更新规则 $\eta$ 和环境特定的超参数 $\alpha$：

$$ \eta^* = \arg\max_{\eta} \mathbb{E}_{\mathcal{E} \sim p(\mathcal{E})} \max_{\alpha} \mathbb{E}_{\theta_0 \sim p(\Theta)} [G] \tag{5} $$

实现上，使用一个 Bandit 算法 $p(\alpha|\mathcal{E})$ 来为每个环境采样超参数，并根据回报更新采样概率：

$$ p(\alpha|\mathcal{E}) \propto \exp\left(\frac{R(\alpha,\mathcal{E}) + \rho/\sqrt{N(\alpha,\mathcal{E})}}{\tau}\right) \tag{6} $$
这确保了 LPG 在元训练期间总是配合“合适”的超参数进行学习，减少了梯度的噪声。

3. 实验结果 (Experiments)

3.1 预测语义的发现

LPG 发现了什么？它是否重新发明了 Value Function？
实验表明，尽管没有强制要求，LPG 发现的预测向量 $y$ 确实编码了类似价值函数的信息。

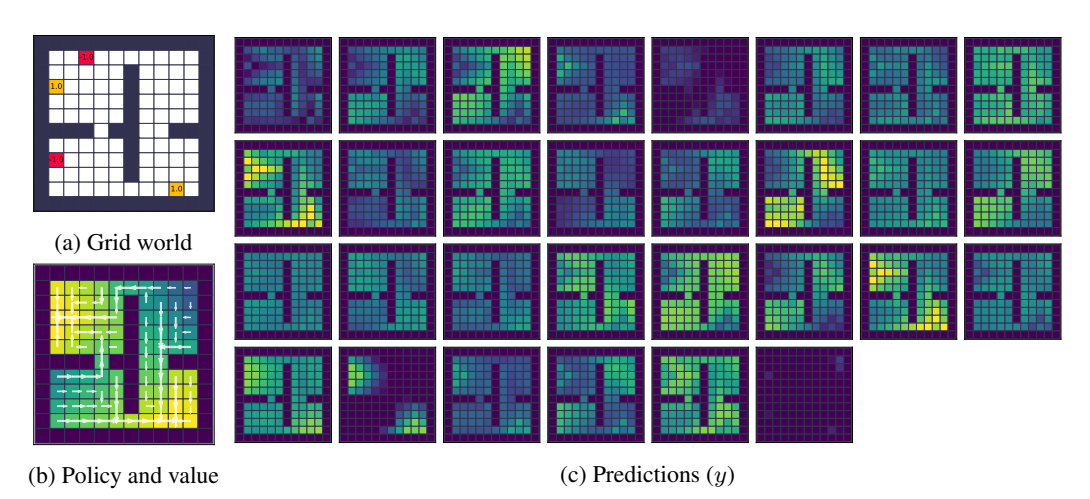
图 4: 预测可视化。(c) 展示了 $y$ 向量在网格世界中的激活情况，可以看到它能够像价值函数一样在空间上传播奖励信号。

进一步的回归分析显示，$y$ 向量中包含了不同时间尺度（不同折扣因子）的价值信息，甚至比标准的 TD($\lambda$) 包含的信息更丰富。

3.2 泛化到 Atari 游戏

这是论文最令人惊讶的结果。LPG 仅在简单的 Grid World 和 Chain MDP 等玩具环境中训练，却能直接应用到从未见过的、视觉复杂的 Atari 游戏中。

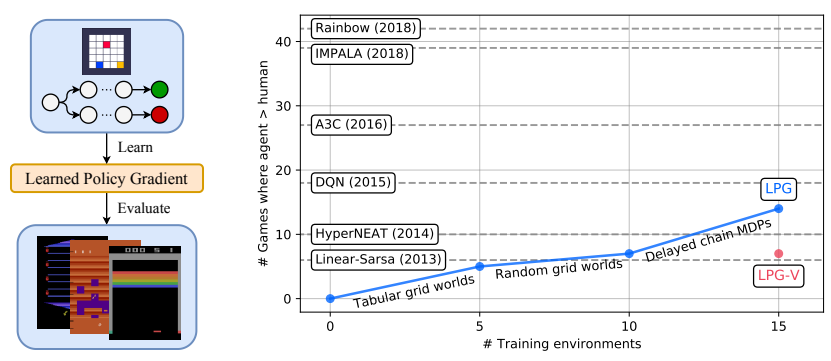
图 9: 从玩具环境到 Atari 的泛化。随着训练环境数量的增加，LPG 在 Atari 上的表现显著提升，甚至在某些游戏中超越了 A2C 和 DQN。

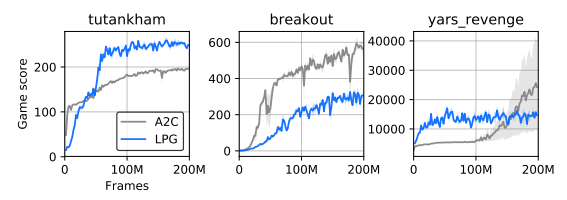
图 8: Atari 游戏上的学习曲线。LPG (蓝色) 在某些游戏上表现优于 A2C (橙色)。

4. 结论 (Conclusion)

LPG 展示了完全从数据中发现通用 RL 算法的可能性。它不仅学会了策略更新规则，还自发地重新发现了“价值函数”和“Bootstrapping”的概念，以此来处理长期信用分配问题。其在 Atari 游戏上的零样本泛化能力（Zero-shot Generalization）表明，通过精心设计的一组小型基础环境，我们可以提炼出极其通用的智能体学习规则。