Meta Learning Backpropagation And Improving It

会议: NeurIPS 2021

时间：2022-03

链接：https://arxiv.org/abs/2012.14905

Abstract

许多神经网络的元学习概念被提出，如学习重编程快速权重（fast weights）、Hebbian可塑性、学习到的学习规则和元循环神经网络（Meta RNN）。本文提出了变量共享元学习 (Variable Shared Meta Learning, VSML)，统一了上述概念。VSML表明，仅通过神经网络中的简单权重共享和稀疏性，就足以以可复用的方式表达强大的学习算法（Learning Algorithms, LAs）。

VSML的一个简单实现是将神经网络的权重替换为微小的LSTM。这允许仅通过前向传递（forward-mode）来实现反向传播（Backpropagation, BP）算法。它甚至可以元学习出不同于在线反向传播的新LAs，并且能够泛化到元训练分布之外的数据集（例如从MNIST泛化到Fashion MNIST），而无需显式的梯度计算。分析表明，VSML元学习到的LAs通过快速关联进行学习，这与梯度下降在性质上是不同的。

1. Introduction

第一段：首先所谓的meta-learning就是learning the learning algorithm itself。然后掰扯了一下meta-learning学出来的策略和人工的的泛化性。然后Unfortunately, 它们还是依赖大量人为设计的规则和inner-loop。

第二段：说自己的VSML。

2. Background

把deep learning-based meta-learning分为了两类：

1. Fast weight programmers & Learned learning rules (FWPs / LLRs)
2. Black-box learning in activations (Meta RNNs)

3. Variable Shared Meta Learning (VSML)

VSML 的目标: 结合 Meta RNNs 的简单性和 FWPs/LLRs 的 $|V^L| \gg |V^M|$ 特性。

3.1 VSML 的三种视角

VSML 可以被理解为以下三种等价的视角（见下图）：

• A. 具有稀疏共享权重矩阵的单个 Meta RNN: 最通用的描述。
• B. RNN 之间的消息传递: 将权重矩阵设计为简单的共享和稀疏模式，对应于多个共享参数的 RNN 之间交换信息。
• C. 具有学习更新的复杂神经元: 当选择特定的 RNN 连接方式时，这些 RNN 的状态/激活值 $V^L$ 可以解释为传统 NN 的权重，从而模糊了权重和激活之间的界限。

3.2 形式化定义 (Mathematical Formulation)

基础 RNN 更新

考虑一个标准的 RNN，隐藏状态 $s \in \mathbb{R}^N$，更新公式为：
$$s_j \leftarrow f_{\text{RNN}}(s)_j = \sigma(\sum_i s_i W_{ij}) \tag{1}$$
其中 $W \in \mathbb{R}^{N \times N}$。

引入变量共享 (Variable Sharing)

我们在两个大小为 $A, B$ 的轴上复制计算，得到状态 $s \in \mathbb{R}^{A \times B \times N}$。对于 $a \in \{1, \dots, A\}, b \in \{1, \dots, B\}$：
$$s_{abj} \leftarrow f_{\text{RNN}}(s_{ab})_j = \sigma(\sum_i s_{abi} W_{ij}) \tag{2}$$
这可以看作是在二维网格上排列的多个独立 RNN，它们共享参数 $W$。

VSML 作为 RNN 间的消息传递 (视角 B)

为了连接这些独立的 RNN，引入消息传递机制：
$$s_{ab} \leftarrow f_{\text{RNN}}(s_{ab}, \overrightarrow{m}_a) \tag{3}$$
其中消息 $\overrightarrow{m}_b = \sum_{a'} f_{\overrightarrow{m}}(s_{a'b})$ 作为额外输入。这里 $f_{\overrightarrow{m}}$ 是一个线性变换。
求和操作模拟了标准 NN 中权重的连接方式。对于简单的线性变换矩阵 $C \in \mathbb{R}^{N \times N}$，公式 (3) 可以写为：
$$s_{abj} \leftarrow \sigma(\sum_{i} s_{abi} W_{ij} + \sum_{a',i} s_{a'ai} C_{ij}) \tag{4}$$
这是 VSML 的最小版本，元参数为 $V_M := (W, C)$。

VSML 作为稀疏共享权重矩阵的 Meta RNN (视角 A)

公式 (4) 等价于一个具有稀疏共享权重矩阵 $\tilde{W}$ 的单个大 RNN：
$$s_{abj} \leftarrow \sigma(\sum_{c,d,i} s_{cdi} \tilde{W}_{cdiabj}) \tag{5}$$
其中 $\tilde{W}$ 满足：
$$\tilde{W}_{cdiabj} = \begin{cases} C_{ij}, & \text{if } d = a \land (d \neq b \lor c \neq a) \\ W_{ij}, & \text{if } d \neq a \land d = b \land c = a \\ C_{ij} + W_{ij}, & \text{if } d = a \land d = b \land c = a \\ 0, & \text{otherwise} \end{cases} \tag{6}$$
这对应于图 1a 中的可视化。

VSML 作为复杂神经元 (视角 C)

在视角 C 中，每个子 RNN ($s_{ab}$) 对应于标准 NN 中的一个权重。
* $V_M$ (Meta Variables): RNN 的参数，定义了“权重”的性质、它们如何参与神经计算以及它们如何更新（学习算法）。
* $V_L$ (Learned Variables): RNN 的状态，代表具体的权重值。

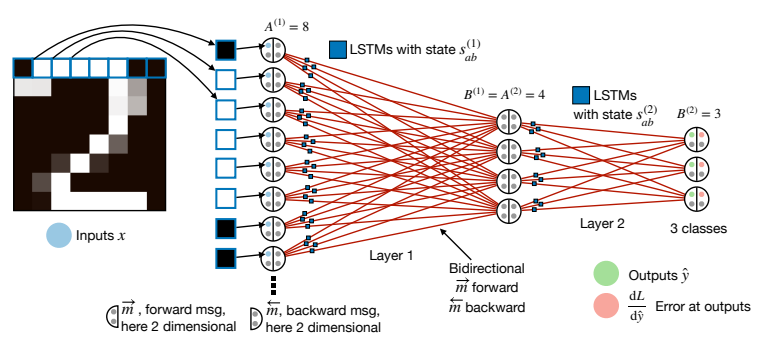
图 2: VSML 的神经解释。标准 NN 的权重被替换为共享参数的微型 LSTM。信息通过多维消息 $\overrightarrow{m}$ (前向) 和 $\overleftarrow{m}$ (后向) 在网络中流动。

3.3 堆叠 VSML RNN 和输入馈送

为了构建类似多层前馈网络（FNN）的结构，可以堆叠多个 VSML RNN 层。
第 $k$ 层的状态为 $s^{(k)}$，层大小为 $A^{(k)}, B^{(k)}$，约束 $A^{(k)} = B^{(k-1)}$。
为了支持反向传播等算法，引入后向消息 (Backward Message) $\overleftarrow{m}$：

$$s_{ab}^{(k)} \leftarrow f_{\text{RNN}}(s_{ab}^{(k)}, \overrightarrow{m}_a^{(k)}, \overleftarrow{m}_b^{(k)}) \tag{7}$$

其中：
* 前向消息: $\overrightarrow{m}_{b}^{(k+1)} := \sum_{a'} f_{\overrightarrow{m}}(s_{a'b}^{(k)})$ (类似于神经元的激活输出)
* 后向消息: $\overleftarrow{m}_{a}^{(k-1)} := \sum_{b'} f_{\overleftarrow{m}}(s_{ab'}^{(k)})$ (类似于反向传播的误差信号)

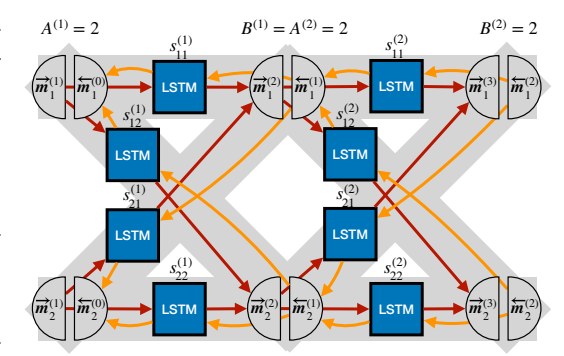
图 3: 带有前向消息 $\overrightarrow{m}$ 和后向消息 $\overleftarrow{m}$ 的两层 VSML 结构。

数据输入与输出:
* 输入 $x$: 初始化第一层的前向消息 $\overrightarrow{m}_{a1}^{(1)} := x_a$。
* 输出 $\hat{y}$: 读取最后一层的前向消息 $\hat{y}_a := \overrightarrow{m}_{a1}^{(K+1)}$。
* 误差 $e$: 将误差注入最后一层的后向消息 $\overleftarrow{m}_{b1}^{(K)} := e_b$。

3.4 算法：元学习通用学习算法

VSML 可以通过端到端的元学习从头开始创建 LAs。

Algorithm 1: VSML Meta Training
简述流程：
1. 初始化 LSTM 参数 $V_M$。
2. 循环直到收敛：
* 初始化 LSTM 状态 $V_L = \{s_{ab}^{(k)}\}$ (即“权重”)。
* 对数据集 $D$ 中的序列 $(x, y)$ 进行内循环：
* 设置输入 $\overrightarrow{m}$。
* 通过公式 (7) 更新所有层的状态 $s_{ab}^{(k)}$ (前向/后向/内部动态同时进行)。
* 计算前向消息 $\overrightarrow{m}$ 和后向消息 $\overleftarrow{m}$。
* 计算输出 $\hat{y}$ 和损失 $L$。
* 计算输出误差 $e$ 并设置 $\overleftarrow{m}$。
* 更新 $V_M$: $V_M \leftarrow V_M - \alpha \nabla_{V_M} \sum L$，梯度可以通过 BPTT 或 进化策略 (Evolution Strategies, ES) 获得。

关键点：在元测试（Meta Testing）阶段，没有显式的梯度下降。学习完全由 RNN 的前向动力学（Forward Dynamics）驱动。

4. 实验 (Experiments)

4.1 VSML RNN 实现反向传播 (Learning Algorithm Cloning)

作者首先验证 VSML 是否能够学会实现反向传播算法。
* 方法: 训练 $V_M$ 使 RNN 状态的一部分存储权重 $w$ 和偏置 $b$，计算 $y=\tanh(x)w+b$，并根据 BP 更新 $w, b$。
* 结果: VSML 成功在 RNN 动力学中克隆了 BP。在 MNIST 和 Fashion MNIST 上，无需显式梯度计算即可进行学习。

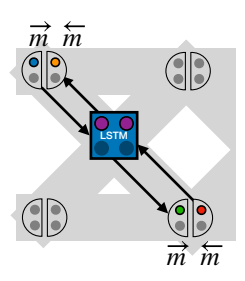
图 4: 学习算法克隆示意图。

4.2 从头元学习监督学习 (Meta Learning from Scratch)

使用进化策略 (ES) 在 MNIST 上元训练 VSML，使其最小化在线分类的累积误差。
* 结果:
* 在 MNIST 上，VSML 的学习速度比在线梯度下降 (SGD) 更快。
* 泛化性: 同一个元学习到的模型可以直接应用到 Fashion MNIST (域外分布) 并成功学习。
* 相比之下，标准的 Meta RNN 严重过拟合，无法泛化。

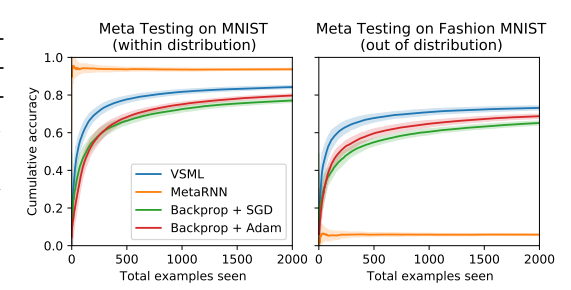
图 6: VSML 在 MNIST 上元训练后，在 MNIST 和 Fashion MNIST (未见过) 上的表现。VSML 展现了强大的泛化能力。

4.3 鲁棒性 (Robustness)

VSML 对输入/输出维度的变化和排列具有鲁棒性。
* 在不同的类别数 (3, 4, 6, 7)、不同的分辨率 (14x14, 28x28, 32x32) 和随机投影下进行元训练。
* 元测试时，模型在未见过的配置下表现良好。

4.4 跨数据集泛化 (Varying Datasets)

在多个数据集（MNIST, Fashion MNIST, EMNIST, KMNIST, Random, Sum Sign）的子集上进行元训练，并在其他数据集上测试。
* VSML 能够泛化到完全未见过的任务（如 Random 和 Sum Sign）。
* 表现优于 Meta RNN, Hebbian Fast Weights 和 External Memory baselines。

5. 分析 (Analysis)

VSML 如何学习？
通过内省（Introspection）分析，作者比较了 VSML 和 SGD 的行为。
* 快速关联 (Fast Association): VSML 倾向于在第一次犯错后，立即以高置信度修正预测。它似乎能够快速将新输入与标签进行关联。
* SGD: 学习速度较慢，需要多次迭代或更小的学习率才能收敛，且容易遗忘。

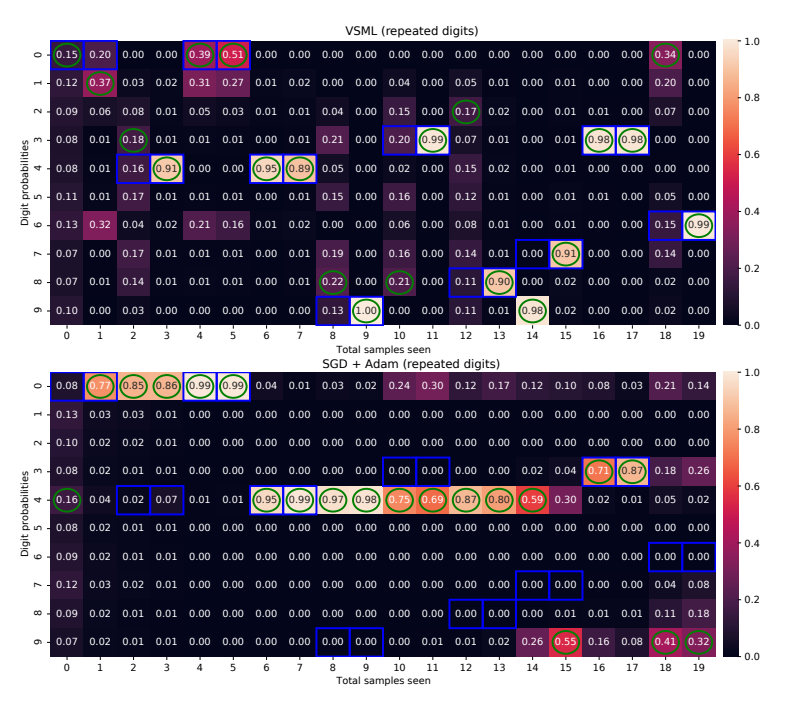
图 9: VSML (上) 与 SGD (下) 的对比。VSML 能够迅速纠正错误并保持高置信度，而 SGD 学习缓慢。

6. 结论 (Conclusion)

• VSML 是一种利用权重共享和稀疏性的元学习原则。
• 它将神经网络的权重替换为共享参数的微型 LSTM。
• 它可以克隆反向传播算法，仅通过 RNN 的前向传播实现学习。
• 它能够从头元学习出通用的学习算法，这些算法比 SGD 更具样本效率，且能泛化到未见过的分布（Out-of-Distribution Generalization）。
• VSML 的学习机制主要基于快速关联，与梯度下降有质的区别。