title: Evolving Artificial Neural Networks
source_pdf: /home/lzr/code/thesis-reading/Neuroevolution/Chapter 3/Evolving Artificial Neural Networks/Evolving Artificial Neural Networks.pdf

Evolving Artificial Neural Networks

XIN YAO, SENIOR MEMBER, IEEE

Invited Paper

Learning and evolution are two fundamental forms of adaptation. There has been a great interest in combining learning and evolution with artificial neural networks (ANN's) in recent years. This paper: 1) reviews different combinations between ANN's and evolutionary algorithms (EA's), including using EA's to evolve ANN connection weights, architectures, learning rules, and input features; 2) discusses different search operators which have been used in various EA's; and 3) points out possible future research directions. It is shown, through a considerably large literature review, that combinations between ANN's and EA's can lead to significantly better intelligent systems than relying on ANN's or EA's alone.

Keywords—Evolutionary computation, intelligent systems, neural networks.

I. INTRODUCTION

Evolutionary artificial neural networks (EANN's) refer to a special class of artificial neural networks (ANN's) in which evolution is another fundamental form of adaptation in addition to learning [1]–[5]. Evolutionary algorithms (EA's) are used to perform various tasks, such as connection weight training, architecture design, learning rule adaptation, input feature selection, connection weight initialization, rule extraction from ANN's, etc. One distinct feature of EANN's is their adaptability to a dynamic environment. In other words, EANN's can adapt to an environment as well as changes in the environment. The two forms of adaptation, i.e., evolution and learning in EANN's, make their adaptation to a dynamic environment much more effective and efficient. In a broader sense, EANN's can be regarded as a general framework for adaptive systems, i.e., systems that can change their architectures and learning rules appropriately without human intervention.

This paper is most concerned with exploring possible benefits arising from combinations between ANN's and EA's. Emphasis is placed on the design of intelligent systems based on ANN's and EA's. Other combinations

Manuscript received July 10, 1998; revised February 18, 1999. This work was supported in part by the Australian Research Council through its small grant scheme.

The author is with the School of Computer Science, University of Birmingham, Edgbaston, Birmingham B15 2TT U.K. (e-mail: xin@cs.bham.ac.uk).

Publisher Item Identifier S 0018-9219(99)06906-6.

between ANN's and EA's for combinatorial optimization will be mentioned but not discussed in detail.

A. Artificial Neural Networks

1) Architectures: An ANN consists of a set of processing elements, also known as neurons or nodes, which are interconnected. It can be described as a directed graph in which each node i performs a transfer function $f_i$ of the form

$$y_i = f_i \left( \sum_{j=1}^n w_{ij} x_j - \theta_i \right) \tag{1}$$

where $y_i$ is the output of the node i, $x_j$ is the jth input to the node, and $w_{ij}$ is the connection weight between nodes i and j. $\theta_i$ is the threshold (or bias) of the node. Usually, $f_i$ is nonlinear, such as a heaviside, sigmoid, or Gaussian function.

ANN's can be divided into feedforward and recurrent classes according to their connectivity. An ANN is feedforward if there exists a method which numbers all the nodes in the network such that there is no connection from a node with a large number to a node with a smaller number. All the connections are from nodes with small numbers to nodes with larger numbers. An ANN is recurrent if such a numbering method does not exist.

In (1), each term in the summation only involves one input $x_j$ . High-order ANN's are those that contain high-order nodes, i.e., nodes in which more than one input are involved in some of the terms of the summation. For example, a second-order node can be described as

$$y_i = f_i \left( \sum_{j,k=1}^n w_{ijk} x_j x_k - \theta_i \right)$$

where all the symbols have similar definitions to those in (1).

The architecture of an ANN is determined by its topological structure, i.e., the overall connectivity and transfer function of each node in the network.

• 1. Generate the initial population G(0) at random, and set i = 0;
• 1. REPEAT
• (a) Evaluate each individual in the population;
• (b) Select parents from G(i) based on their fitness in G(i);
• (c) Apply search operators to parents and produce offspring which form G(i+1);
• (d) i = i + 1;
• 1. UNTIL 'termination criterion' is satisfied

Fig. 1. A general framework of EA's.

2) Learning in ANN's: Learning in ANN's is typically accomplished using examples. This is also called "training" in ANN's because the learning is achieved by adjusting the connection weights1 in ANN's iteratively so that trained (or learned) ANN's can perform certain tasks. Learning in ANN's can roughly be divided into supervised, unsupervised, and reinforcement learning. Supervised learning is based on direct comparison between the actual output of an ANN and the desired correct output, also known as the target output. It is often formulated as the minimization of an error function such as the total mean square error between the actual output and the desired output summed over all available data. A gradient descent-based optimization algorithm such as backpropagation (BP) [6] can then be used to adjust connection weights in the ANN iteratively in order to minimize the error. Reinforcement learning is a special case of supervised learning where the exact desired output is unknown. It is based only on the information of whether or not the actual output is correct. Unsupervised learning is solely based on the correlations among input data. No information on "correct output" is available for learning.

The essence of a learning algorithm is the learning rule, i.e., a weight-updating rule which determines how connection weights are changed. Examples of popular learning rules include the delta rule, the Hebbian rule, the anti-Hebbian rule, and the competitive learning rule [7].

More detailed discussion of ANN's can be found in [7].

B. EA's

EA's refer to a class of population-based stochastic search algorithms that are developed from ideas and principles of natural evolution. They include evolution strategies (ES) [8], [9], evolutionary programming (EP) [10], [11], [12], and genetic algorithms (GA's) [13], [14]. One important feature of all these algorithms is their population-based search strategy. Individuals in a population compete and exchange information with each other in order to perform certain tasks. A general framework of EA's can be described by Fig. 1.

EA's are particularly useful for dealing with large complex problems which generate many local optima. They are less likely to be trapped in local minima than traditional

$^{1}$ Thresholds (biases) can be viewed as connection weights with fixed input -1.

gradient-based search algorithms. They do not depend on gradient information and thus are quite suitable for problems where such information is unavailable or very costly to obtain or estimate. They can even deal with problems where no explicit and/or exact objective function is available. These features make them much more robust than many other search algorithms. Fogel [15] and Bäck et al. [16] give a good introduction to various evolutionary algorithms for optimization.

C. Evolution in EANN's

Evolution has been introduced into ANN's at roughly three different levels: connection weights; architectures; and learning rules. The evolution of connection weights introduces an adaptive and global approach to training, especially in the reinforcement learning and recurrent network learning paradigm where gradient-based training algorithms often experience great difficulties. The evolution of architectures enables ANN's to adapt their topologies to different tasks without human intervention and thus provides an approach to automatic ANN design as both ANN connection weights and structures can be evolved. The evolution of learning rules can be regarded as a process of "learning to learn" in ANN's where the adaptation of learning rules is achieved through evolution. It can also be regarded as an adaptive process of automatic discovery of novel learning rules.

D. Organization of the Article

The remainder of this paper is organized as follows. Section II discusses the evolution of connection weights. The aim is to find a near-optimal set of connection weights globally for an ANN with a fixed architecture using EA's. Various methods of encoding connection weights and different search operators used in EA's will be discussed. Comparisons between the evolutionary approach and conventional training algorithms, such as BP, will be made. In general, no single algorithm is an overall winner for all kinds of networks. The best training algorithm is problem dependent.

Section III is devoted to the evolution of architectures, i.e., finding a near-optimal ANN architecture for the tasks at hand. It is known that the architecture of an ANN determines the information processing capability of the ANN. Architecture design has become one of the most

• 1. Decode each individual (genotype) in the current generation into a set of connection weights and construct a corresponding ANN with the weights.
• 1. Evaluate each ANN by computing its total mean square error between actual and target outputs. (Other error functions can also be used.) The fitness of an individual is determined by the error. The higher the error, the lower the fitness. The optimal mapping from the error to the fitness is problem dependent. A regularization term may be included in the fitness function to penalize large weights.
• 1. Select parents for reproduction based on their fitness.
• 1. Apply search operators, such as crossover and/or mutation, to parents to generate offspring, which form the next generation.

Fig. 2. A typical cycle of the evolution of connection weights.

important tasks in ANN research and application. Two most important issues in the evolution of architectures, i.e., the representation and search operators used in EA's, will be addressed in this section. It is shown that evolutionary algorithms relying on crossover operators do not perform very well in searching for a near-optimal ANN architecture. Reasons and empirical results will be given in this section to explain why this is the case.

If imagining ANN's connection weights and architectures as their "hardware," it is easier to understand the importance of the evolution of ANN's "software"—learning rules. Section IV addresses the evolution of learning rules in ANN's and examines the relationship between learning and evolution, e.g., how learning guides evolution and how learning itself evolves. It is demonstrated that an ANN's learning ability can be improved through evolution. Although research on this topic is still in its early stages, further studies will no doubt benefit research in ANN's and machine learning as a whole.

Section V summarizes some other forms of combinations between ANN's and EA's. They do not intend to be exhaustive, simply indicative. They demonstrate the breadth of possible combinations between ANN's and EA's.

Section VI first describes a general framework of EANN's in terms of adaptive systems where interactions among three levels of evolution are considered. The framework provides a common basis for comparing different EANN models. The section then gives a brief summary of the paper and concludes with a few remarks.

II. THE EVOLUTION OF CONNECTION WEIGHTS

Weight training in ANN's is usually formulated as minimization of an error function, such as the mean square error between target and actual outputs averaged over all examples, by iteratively adjusting connection weights. Most training algorithms, such as BP and conjugate gradient algorithms [7], [17]–[19], are based on gradient descent. There have been some successful applications of BP in various areas [20]–[22], but BP has drawbacks due to its use of gradient descent [23], [24]. It often gets trapped in a local minimum of the error function and is incapable of finding

a global minimum if the error function is multimodal and/or nondifferentiable. A detailed review of BP and other learning algorithms can be found in [7], [17], and [25].

One way to overcome gradient-descent-based training algorithms' shortcomings is to adopt EANN's, i.e., to formulate the training process as the evolution of connection weights in the environment determined by the architecture and the learning task. EA's can then be used effectively in the evolution to find a near-optimal set of connection weights globally without computing gradient information. The fitness of an ANN can be defined according to different needs. Two important factors which often appear in the fitness (or error) function are the error between target and actual outputs and the complexity of the ANN. Unlike the case in gradient-descent-based training algorithms, the fitness (or error) function does not have to be differentiable or even continuous since EA's do not depend on gradient information. Because EA's can treat large, complex, nondifferentiable, and multimodal spaces, which are the typical case in the real world, considerable research and application has been conducted on the evolution of connection weights [24], [26]–[112].

The evolutionary approach to weight training in ANN's consists of two major phases. The first phase is to decide the representation of connection weights, i.e., whether in the form of binary strings or not. The second one is the evolutionary process simulated by an EA, in which search operators such as crossover and mutation have to be decided in conjunction with the representation scheme. Different representations and search operators can lead to quite different training performance. A typical cycle of the evolution of connection weights is shown in Fig. 2. The evolution stops when the fitness is greater than a predefined value (i.e., the training error is smaller than a certain value) or the population has converged.

A. Binary Representation

The canonical genetic algorithm (GA) [13], [14] has always used binary strings to encode alternative solutions, often termed chromosomes. Some of the early work in evolving ANN connection weights followed this approach

Fig. 3. (a) An ANN with connection weights shown. (b) A binary representation of the weights, assuming that each weight is represented by four bits.

[24], [26], [28], [37], [38], [41], [52], [53]. In such a representation scheme, each connection weight is represented by a number of bits with certain length. An ANN is encoded by concatenation of all the connection weights of the network in the chromosome.

A heuristic concerning the order of the concatenation is to put connection weights to the same hidden/output node together. Hidden nodes in ANN's are in essence feature extractors and detectors. Separating inputs to the same hidden node far apart in the binary representation would increase the difficulty of constructing useful feature detectors because they might be destroyed by crossover operators. It is generally very difficult to apply crossover operators in evolving connection weights since they tend to destroy feature detectors found during the evolutionary process.

Fig. 3 gives an example of the binary representation of an ANN whose architecture is predefined. Each connection weight in the ANN is represented by 4 bits, the whole ANN is represented by 24 bits where weight 0000 indicates no connection between two nodes.

The advantages of the binary representation lie in its simplicity and generality. It is straightforward to apply classical crossover (such as one-point or uniform crossover) and mutation to binary strings. There is little need to design complex and tailored search operators. The binary representation also facilitates digital hardware implementation of ANN's since weights have to be represented in terms of bits in hardware with limited precision.

There are several encoding methods, such as uniform, Gray, exponential, etc., that can be used in the binary representation. They encode real values using different ranges and precisions given the same number of bits. However, a tradeoff between representation precision and the length of chromosome often has to be made. If too few bits are used to represent each connection weight, training might fail because some combinations of real-valued connection weights cannot be approximated with sufficient accuracy by discrete values. On the other hand, if too many bits are used, chromosomes representing large ANN's will become extremely long and the evolution in turn will become very inefficient.

One of the problems faced by evolutionary training of ANN's is the permutation problem [32], [113], also known as the competing convention problem. It is caused by the

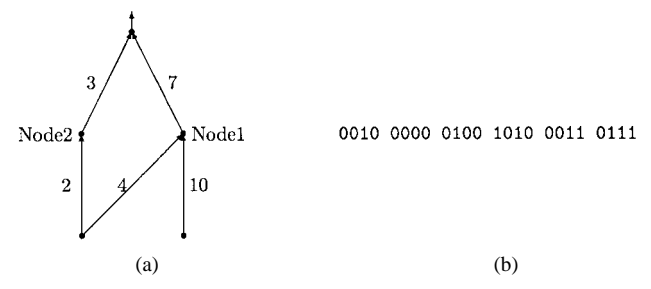
Fig. 4. (a) An ANN which is equivalent to that given in Fig. 3(a). (b) Its binary representation under the same representation scheme.

many-to-one mapping from the representation (genotype) to the actual ANN (phenotype) since two ANN's that order their hidden nodes differently in their chromosomes will still be equivalent functionally. For example, ANN's shown by Figs. 3(a) and 4(a) are equivalent functionally, but they have different chromosomes as shown by Figs. 3(b) and 4(b). In general, any permutation of the hidden nodes will produce functionally equivalent ANN's with different chromosome representations. The permutation problem makes crossover operator very inefficient and ineffective in producing good offspring.

B. Real-Number Representation

There have been some debates on the cardinality of the genotype alphabet. Some have argued that the minimal cardinality, i.e., the binary representation, might not be the best [48], [114]. Formal analysis of nonstandard representations and operators based on the concept of equivalent classes [115], [116] has given representations other than k ary strings a more solid theoretical foundation. Real numbers have been proposed to represent connection weights directly, i.e., one real number per connection weight [27], [29], [30], [48], [63]–[65], [74], [95], [96], [102], [110], [111], [117], [118]. For example, a real-number representation of the ANN given by Fig. 3(a) could be (4.0, 10.0, 2.0, 0.0, 7.0, 3.0).

As connection weights are represented by real numbers, each individual in an evolving population will be a real vector. Traditional binary crossover and mutation can no longer be used directly. Special search operators have to be designed. Montana and Davis [27] defined a large number of tailored genetic operators which incorporated many heuristics about training ANN's. The idea was to retain useful feature detectors formed around hidden nodes during evolution. Their results showed that the evolutionary training approach was much faster than BP for the problems they considered. Bartlett and Downs [30] also demonstrated that the evolutionary approach was faster and had better scalability than BP.

A natural way to evolve real vectors would be to use EP or ES since they are particularly well-suited for treating continuous optimization. Unlike GA's, the primary search operator in EP and ES is mutation. One of the major advantages of using mutation-based EA's is that they can reduce the negative impact of the permutation problem. Hence the evolutionary process can be more efficient. There

have been a number of successful examples of applying EP or ES to the evolution of ANN connection weights [29], [63]–[65], [67], [68], [95], [96], [102], [106], [111], [117], [119], [120]. In these examples, the primary search operator has been Gaussian mutation. Other mutation operators, such as Cauchy mutation [121], [122], can also be used. EP and ES also allow self adaptation of strategy parameters. Evolving connection weights by EP can be implemented as follows.

• 1) Generate an initial population of $\mu$ individuals at random and set k=1. Each individual is a pair of real-valued vectors, $(\mathbf{w}_i,\eta_i), \ \forall i \in \{1,\ldots,\mu\}$ , where $\mathbf{w}_i$ 's are connection weight vectors and $\eta_i$ 's are variance vectors for Gaussian mutations (also known as strategy parameters in self-adaptive EA's). Each individual corresponds to an ANN.
• 2) Each individual $(\mathbf{w}_i, \eta_i)$ , $i = 1, ..., \mu$ , creates a single offspring $(\mathbf{w}_i', \eta_i')$ by: for j = 1, ..., n

$$\eta_i'(j) = \eta_i(j) \exp(\tau' N(0,1) + \tau N_j(0,1)) \tag{2} $$

$$w_i'(j) = w_i(j) + \eta_i'(j)N_j(0,1) \tag{3} $$

where $w_i(j)$ , $w_i'(j)$ , $\eta_i(j)$ , and $\eta_i'(j)$ denote the jth component of the vectors $\mathbf{w}_i$ , $\mathbf{w}_i'$ , $\eta_i$ and $\eta_i'$ , respectively. N(0,1) denotes a normally distributed one-dimensional random number with mean zero and variance one. $N_j(0,1)$ indicates that the random number is generated anew for each value of j. The parameters $\tau$ and $\tau'$ are commonly set to $(\sqrt{2\sqrt{n}})^{-1}$ and $(\sqrt{2n})^{-1}$ [15], [123]. $N_j(0,1)$ in (3) may be replaced by Cauchy mutation [121], [122], [124] for faster evolution.

• Determine the fitness of every individual, including all parents and offspring, based on the training error. Different error functions may be used here.
• 4) Conduct pairwise comparison over the union of parents $(\mathbf{w}_i, \eta_i)$ and offspring $(\mathbf{w}_i', \eta_i')$ , $\forall i \in \{1, \dots, \mu\}$ . For each individual, q opponents are chosen uniformly at random from all the parents and offspring. For each comparison, if the individual's fitness is no smaller than the opponent's, it receives a "win." Select $\mu$ individuals out of $(\mathbf{w}_i, \eta_i)$ and $(\mathbf{w}_i', \eta_i')$ , $\forall i \in \{1, \dots, \mu\}$ , that have most wins to form the next generation. (This tournament selection scheme may be replaced by other selection schemes, such as [1251.)
• 5) Stop if the halting criterion is satisfied; otherwise, k = k + 1 and go to Step 2).

C. Comparison Between Evolutionary Training and Gradient-Based Training

As indicated at the beginning of Section II, the evolutionary training approach is attractive because it can handle the global search problem better in a vast, complex, multimodal, and nondifferentiable surface. It does not depend on gradient information of the error (or fitness) function and thus is particularly appealing when this information

is unavailable or very costly to obtain or estimate. For example, the evolutionary approach has been used to train recurrent ANN's [41], [60], [65], [100], [102], [103], [106], [117], [126]–[128], higher order ANN's [52], [53], and fuzzy ANN's [76], [77], [129], [130]. Moreover, the same EA can be used to train many different networks regardless of whether they are feedforward, recurrent, or higher order ANN's. The general applicability of the evolutionary approach saves a lot of human efforts in developing different training algorithms for different types of ANN's.

The evolutionary approach also makes it easier to generate ANN's with some special characteristics. For example, the ANN's complexity can be decreased and its generalization increased by including a complexity (regularization) term in the fitness function. Unlike the case in gradient-based training, this term does not need to be differentiable or even continuous. Weight sharing and weight decay can also be incorporated into the fitness function easily.

Evolutionary training can be slow for some problems in comparison with fast variants of BP [131] and conjugate gradient algorithms [19], [132]. However, EA's are generally much less sensitive to initial conditions of training. They always search for a globally optimal solution, while a gradient descent algorithm can only find a local optimum in a neighborhood of the initial solution.

For some problems, evolutionary training can be significantly faster and more reliable than BP [30], [34], [40], [63], [83], [89]. Prados [34] described a GA-based training algorithm which is "significantly faster than methods that use the generalized delta rule (GDR)." For the three tests reported in his paper [34], the GA-based training algorithm "took a total of about 3 hours and 20 minutes, and the GDR took a total of about 23 hours and 40 minutes." Bartlett and Downs [30] also gave a modified GA which was "an order of magnitude" faster than BP for the 7-bit parity problem. The modified GA seemed to have better scalability than BP since it was "around twice" as slow as BP for the XOR problem but faster than BP for the larger 7-bit parity problem.

Interestingly, quite different results were reported by Kitano [133]. He found that the GA–BP method, a technique that runs a GA first and then BP, "is, at best, equally efficient to faster variants of back propagation in very small scale networks, but far less efficient in larger networks." The test problems he used included the XOR problem, various size encoder/decoder problems, and the two-spiral problem. However, there have been many other papers which report excellent results using hybrid evolutionary and gradient descent algorithms [32], [67], [70], [71], [74], [80], [81], [86], [103], [105], [110]–[112].

The discrepancy between two seemingly contradictory results can be attributed at least partly to the different EA's and BP compared. That is, whether the comparison is between a classical binary GA and a fast BP algorithm, or between a fast EA and a classical BP algorithm. The discrepancy also shows that there is no clear winner in terms of the best training algorithm. The best one is always problem dependent. This is certainly true according to the

no-free-lunch theorem [134]. In general, hybrid algorithms tend to perform better than others for a large number of problems.

D. Hybrid Training

Most EA's are rather inefficient in fine-tuned local search although they are good at global search. This is especially true for GA's. The efficiency of evolutionary training can be improved significantly by incorporating a local search procedure into the evolution, i.e., combining EA's global search ability with local search's ability to fine tune. EA's can be used to locate a good region in the space and then a local search procedure is used to find a near-optimal solution in this region. The local search algorithm could be BP [32], [133] or other random search algorithms [30], [135]. Hybrid training has been used successfully in many application areas [32], [67], [70], [71], [74], [80], [81], [86], [103], [105], [110]–[112].

Lee [81] and many others [32], [136]–[138] used GA's to search for a near-optimal set of initial connection weights and then used BP to perform local search from these initial weights. Their results showed that the hybrid GA/BP approach was more efficient than either the GA or BP algorithm used alone. If we consider that BP often has to run several times in practice in order to find good connection weights due to its sensitivity to initial conditions, the hybrid training algorithm will be quite competitive. Similar work on the evolution of initial weights has also been done on competitive learning neural networks [139] and Kohonen networks [140].

It is interesting to consider finding good initial weights as locating a good region in the weight space. Defining that basin of attraction of a local minimum as being composed of all the points, sets of weights in this case, which can converge to the local minimum through a local search algorithm, then a global minimum can easily be found by the local search algorithm if an EA can locate a point, i.e., a set of initial weights, in the basin of attraction of the global minimum. Fig. 5 illustrates a simple case where there is only one connection weight in the ANN. If an EA can find an initial weight such as $w_{I2}$ , it would be easy for a local search algorithm to arrive at the globally optimal weight $w_B$ even though $w_{I2}$ itself is not as good as $w_{I1}$ .

III. THE EVOLUTION OF ARCHITECTURES

Section II assumed that the architecture of an ANN is predefined and fixed during the evolution of connection weights. This section discusses the design of ANN architectures. The architecture of an ANN includes its topological structure, i.e., connectivity, and the transfer function of each node in the ANN. As indicated in the beginning of this paper, architecture design is crucial in the successful application of ANN's because the architecture has significant impact on a network's information processing capabilities. Given a learning task, an ANN with only a few connections and linear nodes may not be able to perform the task at all due to its limited capability, while an ANN with

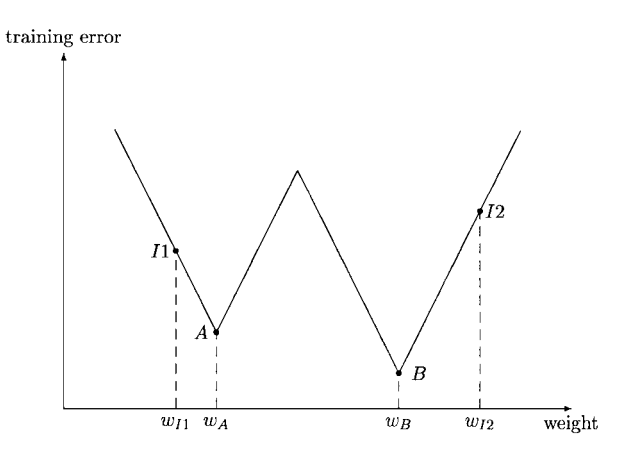
Fig. 5. An illustration of using an EA to find good initial weights such that a local search algorithm can find the globally optimal weights easily. $w_{I2}$ in this figure is an optimal initial weight because it can lead to the global optimum $w_B$ using a local search algorithm.

a large number of connections and nonlinear nodes may overfit noise in the training data and fail to have good generalization ability.

Up to now, architecture design is still very much a human expert's job. It depends heavily on the expert experience and a tedious trial-and-error process. There is no systematic way to design a near-optimal architecture for a given task automatically. Research on constructive and destructive algorithms represents an effort toward the automatic design of architectures [141]–[148]. Roughly speaking, a constructive algorithm starts with a minimal network (network with minimal number of hidden layers, nodes, and connections) and adds new layers, nodes, and connections when necessary during training while a destructive algorithm does the opposite, i.e., starts with the maximal network and deletes unnecessary layers, nodes, and connections during training. However, as indicated by Angeline et al. [149], "Such structural hill climbing methods are susceptible to becoming trapped at structural local optima." In addition, they "only investigate restricted topological subsets rather than the complete class of network architectures" [149].

Design of the optimal architecture for an ANN can be formulated as a search problem in the architecture space where each point represents an architecture. Given some performance (optimality) criteria, e.g., lowest training error, lowest network complexity, etc., about architectures, the performance level of all architectures forms a discrete surface in the space. The optimal architecture design is equivalent to finding the highest point on this surface. There are several characteristics of such a surface as indicated by Miller et al. [150] which make EA's a better candidate for searching the surface than those constructive and destructive algorithms mentioned above. These characteristics are [150]:

• the surface is infinitely large since the number of possible nodes and connections is unbounded;

• the surface is nondifferentiable since changes in the number of nodes or connections are discrete and can have a discontinuous effect on EANN's performance;

• Decode each individual in the current generation into an architecture. If the indirect encoding scheme is used, further detail of the architecture is specified by some developmental rules or a training process.

• Train each ANN with the decoded architecture by a predefined learning rule (some parameters of the learning rule could be evolved during training) starting from different sets of random initial connection weights and, if any, learning rule parameters.
• Compute the fitness of each individual (encoded architecture) according to the above training result and other performance criteria such as the complexity of the architecture.
• 1. Select parents from the population based on their fitness.
• 1. Apply search operators to the parents and generate offspring which form the next generation.

Fig. 6. A typical cycle of the evolution of architectures.

• the surface is complex and noisy since the mapping from an architecture to its performance is indirect, strongly epistatic, and dependent on the evaluation method used;
• 4) the surface is deceptive since similar architectures may have quite different performance;
• 5) the surface is multimodal since different architectures may have similar performance.

Similar to the evolution of connection weights, two major phases involved in the evolution of architectures are the genotype representation scheme of architectures and the EA used to evolve ANN architectures. One of the key issues in encoding ANN architectures is to decide how much information about an architecture should be encoded in the chromosome. At one extreme, all the details, i.e., every connection and node of an architecture, can be specified by the chromosome. This kind of representation scheme is called direct encoding. At the other extreme, only the most important parameters of an architecture, such as the number of hidden layers and hidden nodes in each layer, are encoded. Other details about the architecture are left to the training process to decide. This kind of representation scheme is called indirect encoding. After a representation scheme has been chosen, the evolution of architectures can progress according to the cycle shown in Fig. 6. The cycle stops when a satisfactory ANN is found.

Considerable research on evolving ANN architectures has been carried out in recent years [33], [42], [45], [118], [127], [128], [130], [138], [149]–[225]. Most of the research has concentrated on the evolution of ANN topological structures. Relatively little has been done on the evolution of node transfer functions, let alone the simultaneous evolution of both topological structures and node transfer functions. In this paper, we will analyze the genotypical representation scheme of topological structures in Sections III-A and III-B. For convenience, the term architecture will be used interchangeably with the

term topological structure (topology) in these two sections. Section III-C discusses the evolution of node transfer functions briefly. Then we explain why the simultaneous evolution of ANN connection weights and architectures is beneficial and what search operators should be used in evolving architectures in Section III-D.

A. The Direct Encoding Scheme

Two different approaches have been taken in the direct encoding scheme. The first separates the evolution of architectures from that of connection weights [24], [150], [153], [154], [165], [167], [169], [170]. The second approach evolves architectures and connection weights simultaneously [149], [179], [180], [182], [185]–[200]. This section will focus on the first approach. The second approach will be discussed in Section III-D.

In the first approach, each connection of an architecture is directly specified by its binary representation [24], [150], [153], [154], [165], [167], [169], [170], [202]. For example, an $N \times N$ matrix $C = (c_{ij})_{N \times N}$ can represent an ANN architecture with N nodes, where $c_{ij}$ indicates presence or absence of the connection from node i to node j. We can use $c_{ij} = 1$ to indicate a connection and $c_{ij} = 0$ to indicate no connection. In fact, $c_{ij}$ can represent real-valued connection weights from node i to node j so that the architecture and connection weights can be evolved simultaneously [37], [42], [45], [165], [166], [169]–[171].

Each matrix C has a direct one-to-one mapping to the corresponding ANN architecture. The binary string representing an architecture is the concatenation of rows (or columns) of the matrix. Constraints on architectures being explored can easily be incorporated into such a representation scheme by imposing constraints on the matrix, e.g., a feedforward ANN will have nonzero entries only in the upper-right triangle of the matrix. Figs. 7 and 8 give two examples of the direct encoding scheme of ANN architectures. It is obvious that such an encoding scheme can handle both feedforward and recurrent ANN's.

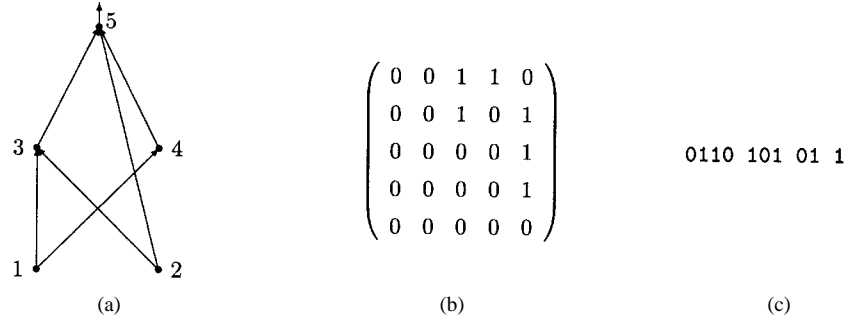
Fig. 7. An example of the direct encoding of a feedforward ANN. (a), (b), and (c) show the architecture, its connectivity matrix, and its binary string representation, respectively. Because only feedforward architectures are under consideration, the binary string representation only needs to consider the upper-right triangle of the matrix.

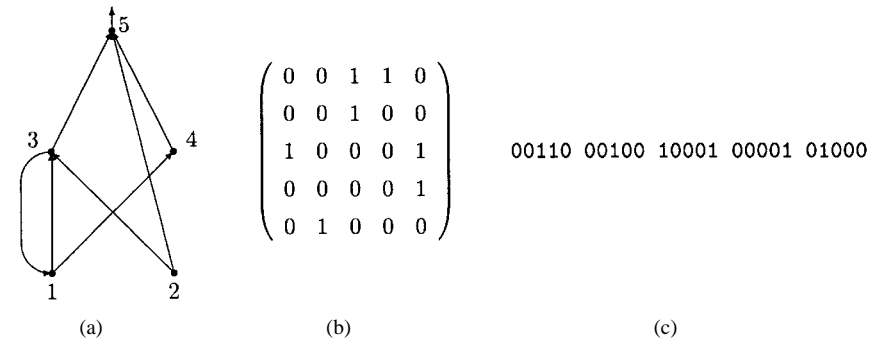
Fig. 8. An example of the direct encoding of a recurrent ANN. (a), (b), and (c) show the architecture, its connectivity matrix, and its binary string representation, respectively.

Fig. 7(a) shows a feedforward ANN with two inputs and one output. Its connectivity matrix is given by Fig. 7(b), where entry $c_{ij}$ indicates the presence or absence of a connection from node i to node j. For example, the first row indicates connections from node 1 to all other nodes. The first two columns are 0's because there is no connection from node 1 to itself and no connection to node 2. However, node 1 is connected to nodes 3 and 4. Hence columns 3 and 4 have 1's. Converting this connectivity matrix to a chromosome is straightforward. We can concatenate all the rows (or columns) and obtain

Since the ANN is feedforward, we only need to represent the upper triangle of the connectivity matrix in order to reduce the chromosome length. The reduced chromosome is given by Fig. 7(c). An EA can then be employed to evolve a population of such chromosomes. In order to evaluate the fitness of each chromosome, we need to convert a chromosome back to an ANN, initialize it with random weights, and train it. The training error will be used to measure the fitness. It is worth noting that the ANN in Fig. 7 has a shortcut connection from the input to output. Such shortcuts pose no problems to the representation and evolution. An EA is capable of exploring all possible connectivities.

Fig. 8 shows a recurrent ANN. Its representation is basically the same as that for feedforward ANN's. The only difference is that no reduction in chromosome length

is possible if we want to explore the whole connectivity space. The EA used to evolve recurrent ANN's can be the same as that used to evolve feedforward ones.

The direct encoding scheme as described above is quite straightforward to implement. It is very suitable for the precise and fine-tuned search of a compact ANN architecture, since a single connection can be added or removed from the ANN easily. It may facilitate rapid generation and optimization of tightly pruned interesting designs that no one has hit upon so far [150].

Another flexibility provided by the evolution of architectures stems from the fitness definition. There is virtually no limitation such as being differentiable or continuous on how the fitness function should be defined at Step 3 in Fig. 6. The training result pertaining to an architecture such as the error and the training time is often used in the fitness function. The complexity measurement such as the number of nodes and connections is also used in the fitness function. As a matter of fact, many criteria based on the information theory or statistics [226]-[228] can readily be introduced into the fitness function without much difficulty. Improvement on ANN's generalization ability can be expected if these criteria are adopted. Schaffer et al. [153] have presented an experiment which showed that an ANN designed by the evolutionary approach had better generalization ability than one trained by BP using a human-designed architecture.

One potential problem of the direct encoding scheme is scalability. A large ANN would require a very large matrix and thus increase the computation time of the evolution. One way to cut down the size of matrices is to use domain knowledge to reduce the search space. For example, if complete connection is to be used between two neighboring layers in a feedforward ANN, its architecture can be encoded by just the number of hidden layers and nodes in each hidden layer. The length of chromosome can be reduced greatly in this case [153], [154]. However, doing so requires sufficient domain knowledge and expertise, which are difficult to obtain in practice. We also run the risk of missing some very good solutions when we restrict the search space manually.

The permutation problem as illustrated by Figs. 3 and 4 in Section II-A still exists and causes unwanted side effects in the evolution of architectures. Because two functionally equivalent ANN's which order their hidden nodes differently have two different genotypical representations, the probability of producing a highly fit offspring by recombining them is often very low. Some researchers thus avoided crossover and adopted only mutations in the evolution of architectures [45], [128], [149], [179], [185]–[197], [217], [223], although it has been shown that crossover may be useful and important in increasing the efficiency of evolution for some problems [48], [113], [212], [229]. Hancock [113] suggested that the permutation problem might "not be as severe as had been supposed" with the population size and the selection mechanism he used because "The increased number of ways of solving the problem outweigh the difficulties of bringing building blocks together." Thierens [101] proposed a genetic encoding scheme of ANN's which can avoid the permutation problem, however, only very limited experimental results were presented. It is worth indicating that most studies on the permutation problem concentrate on the GA used, e.g., genetic operators, population sizes, selection mechanisms, etc. While it is necessary to investigate the algorithm, it is equally important to study the genotypical representation scheme, since the performance surface defined in the beginning of Section III is determined by the representation. More research is needed to further understand the impact of the permutation problem on the evolution of architectures.

B. The Indirect Encoding Scheme

In order to reduce the length of the genotypical representation of architectures, the indirect encoding scheme has been used by many researchers [151], [152], [155], [156], [159], [160], [168], [184], [205], [208], [211], [230]–[232] where only some characteristics of an architecture are encoded in the chromosome. The details about each connection in an ANN is either predefined according to prior knowledge or specified by a set of deterministic developmental rules. The indirect encoding scheme can produce more compact genotypical representation of ANN architectures, but it may not be very good at finding a compact ANN with good generalization ability. Some [151], [230], [231] have argued that the indirect encoding scheme is biologically more plausible than the direct one, because it is impossible for genetic information encoded in

chromosomes to specify independently the whole nervous system according to the discoveries of neuroscience.

1) Parametric Representation: ANN architectures may be specified by a set of parameters such as the number of hidden layers, the number of hidden nodes in each layer, the number of connections between two layers, etc. These parameters can be encoded in various forms in a chromosome. Harp et al. [152], [156] used a "blueprint" to represent an architecture which consists of one or more segments representing an area (layer) and its efferent connectivity (projections). The first and last area are constrained to be the input and output area, respectively. Each segment includes two parts of the information: 1) that about the area itself, such as the number of nodes in the area and the spatial organization of the area, and 2) that about the efferent connectivity. It should be noted that only the connectivity pattern instead of each connection is specified here. The detailed node-to-node connection is specified by implicit developmental rules, e.g., the network instantiation software used by Harp et al. [152], [156]. Similar parametric representation methods with different sets of parameters have also been proposed by others [155], [159]. An interesting aspect of Harp et al.'s work is their combination of learning parameters with architectures in the genotypical representation. The learning parameters can evolve along with architecture parameters. The interaction between the two can be explored through evolution.

Although the parametric representation method can reduce the length of binary chromosome specifying ANN's architectures, EA's can only search a limited subset of the whole feasible architecture space. For example, if we encode only the number of hidden nodes in the hidden layer, we basically assume strictly layered feedforward ANN's with a single hidden layer. We will have to assume two neighboring layers are fully connected as well. In general, the parametric representation method will be most suitable when we know what kind of architectures we are trying to find.

2) Developmental Rule Representation: A quite different indirect encoding method from the above is to encode developmental rules, which are used to construct architectures, in chromosomes [151], [168], [184], [205], [230], [232]. The shift from the direct optimization of architectures to the optimization of developmental rules has brought some benefits, such as more compact genotypical representation, to the evolution of architectures. The destructive effect of crossover will also be lessened since the developmental rule representation is capable of preserving promising building blocks found so far [151]. But this method also has some problems [233].

A developmental rule is usually described by a recursive equation [230] or a generation rule similar to a production rule in a production system with a left-hand side (LHS) and a right-hand side (RHS) [151]. The connectivity pattern of the architecture in the form of a matrix is constructed from a basis, i.e., a single-element matrix, by repetitively applying suitable developmental rules to nonterminal elements in

$$S \longrightarrow \begin{pmatrix} A & B \\ C & D \end{pmatrix}$$

$$A \longrightarrow \begin{pmatrix} a & a \\ a & a \end{pmatrix} \quad B \longrightarrow \begin{pmatrix} i & i \\ i & a \end{pmatrix} \quad C \longrightarrow \begin{pmatrix} i & a \\ a & c \end{pmatrix} \quad D \longrightarrow \begin{pmatrix} a & e \\ a & e \end{pmatrix} \quad \cdots$$

$$a \longrightarrow \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \quad c \longrightarrow \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} \quad e \longrightarrow \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \quad i \longrightarrow \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} \quad \cdots$$

Fig. 9. Examples of some developmental rules used to construct a connectivity matrix. S is the initial element (or state).

the current matrix until the matrix contains only terminal2 elements which indicate the presence or absence of a connection, that is, until a connectivity pattern is fully specified.

Some examples of developmental rule are given in Fig. 9. Each developmental rule consists of a LHS which is a nonterminal element and a RHS which is a 2 2 matrix with either terminal or nonterminal elements. A typical step of constructing a connection matrix is to find rules whose LHS's appear in the current matrix and replace all the appearance with respective RHS's. For example, given a set of rules as described by Fig. 9, where is the starting symbol (state), one step application of these rules will produce the matrix

$$\begin{pmatrix} A & B \\ C & D \end{pmatrix}$$

by replacing with . If we apply these rules again, we can generate the following matrix:

$$\begin{pmatrix} a & a & i & i \\ a & a & i & a \\ i & a & a & e \\ a & c & a & e \end{pmatrix}$$

by replacing with with with , and with . Another step of applying these rules would lead us to the matrix

$$\begin{pmatrix} 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 &$$

by replacing with with with , and with . Since the above matrix consists of ones and zeros only (i.e., terminals only), there will be no further application of developmental rules. The above matrix will be an ANN's connection matrix.

Fig. 10 summarizes the previous three rule-rewriting steps and the final ANN generated according to Fig. 10(d).

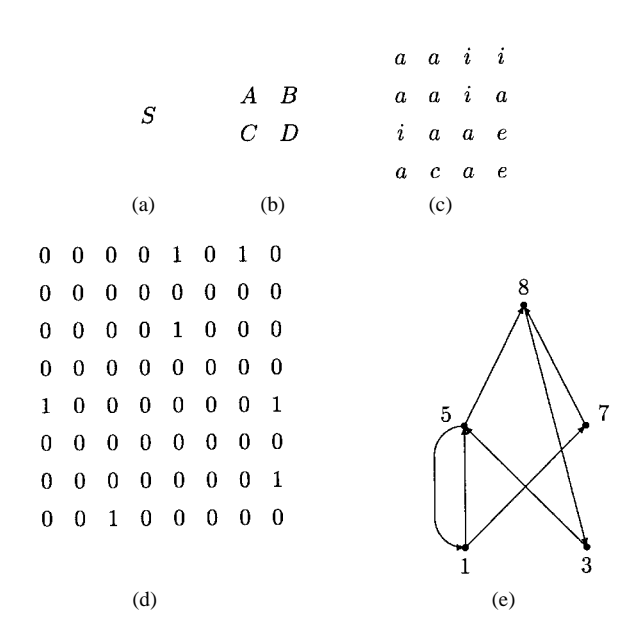
Fig. 10. Development of an EANN architecture using the rules given in Fig. 9: (a) the initial state; (b) step 1; (c) step 2; (d) step 3 when all the entries in the matrix are terminal elements, i.e., either 1 or 0; and (e) the architecture. The nodes in the architecture are numbered from one to eight. Isolated nodes are not shown.

Note that nodes 2, 4, and 6 do not appear in the ANN because they are not connected to any other nodes.

The example described by Figs. 9 and 10 illustrates how an ANN architecture can be defined given a set of rules. The question now is how to get such a set of rules to construct an ANN. One answer is to evolve them. We can encode the whole rule set as an individual [151] (the socalled Pitt approach) or encode each rule as an individual [184] (the so-called Michigan approach). Each rule may be represented by four allele positions corresponding to four elements in the RHS of the rule. The LHS can be represented implicitly by the rule's position in the chromosome. Each position in a chromosome can take one of many different values, depending on how many nonterminal elements (symbols) we use in the rule set. For example, the nonterminals may range from " " to " " and " " to " ." The 16 rules with " " to " " on the LHS and 2 2 matrices with only ones and zeros on the RHS are predefined and do not participate in evolution in order to guarantee that different connectivity patterns can be reached. Since there are 26 different rules, whose LHS is " ," " ," ," ," respectively, a chromosome encoding all of them would need 26 4 104 alleles, four per rule.

² In this paper, a terminal element is either 1 (existence of a connection) or 0 (nonexistence of a connection) and a nonterminal element is a symbol other than 1 and 0. These definitions are slightly different from those used by others [151].

The LHS of a rule is implicitly determined by its position in the chromosome. For example, the rule set in Fig. 9 can be represented by the following chromosome:

ABCDaaaaiiiaiaacaeae...

where the first four elements indicate the RHS of rule "S", the second four indicate the RHS of rule "A," etc.

Some good results from the developmental rule representation method have been reported [151] using various size encoder/decoder problems. However, the method has some limitations. It often needs to predefine the number of rewriting steps. It does not allow recursive rules. It is not very good at evolving detailed connectivity patterns among individual nodes. A compact genotypical representation does not imply a compact phenotypical representation, i.e., a compact ANN architecture. Recent work by Siddigi and Lucas [233] shows that the direct encoding scheme can be at least as good as the developmental rule method. They have reimplemented Kitano's system and discovered that the performance difference between the direct and indirect encoding schemes was not caused by the encoding scheme itself, but by how sparsely connected the initial ANN architectures were in the initial population [151]. The direct encoding scheme achieved the same performance as that achieved by the developmental rule representation when the initial conditions were the same [233].

The developmental rule representation method normally separates the evolution of architectures from that of connection weights. This creates some problems for evolution. Section III-D will discuss these in more detail.

Mjolsness et al. [230] described a similar rule encoding method where rules are represented by recursive equations which specify the growth of connection matrices. Coefficients of these recursive equations, represented by decomposition matrices, are encoded in genotypes and optimized by simulated annealing instead of EA's. Connection weights are optimized along with connectivity by simulated annealing since each entry of a connection matrix can have a real-valued weight. One advantage of using simulated annealing instead of GA's in the evolution is the avoidance of the destructive effect of crossover. Wilson [234] also used simulated annealing in ANN architecture design.

• 3) Fractal Representation: Merrill and Port [231] proposed another method for encoding architectures which is based on the use of fractal subsets of the plane. They argued that the fractal representation of architectures was biologically more plausible than the developmental rule representation. They used three real-valued parameters, i.e., an edge code, an input coefficient, and an output coefficient to specify each node in an architecture. In a sense, this encoding method is closer to the direct encoding scheme rather to the indirect one. Fast simulated annealing [235] was used in the evolution.
• 4) Other Representations: A very different approach to the evolution of architectures has been proposed by Andersen and Tsoi [236]. Their approach is unique in that each individual in a population represents a hidden node rather than the whole architecture. An architecture is built layer by layer, i.e., hidden layers are added one by one if the

current architecture cannot reduce the training error below certain threshold. Each hidden layer is constructed automatically through an evolutionary process which employs the GA with fitness sharing. Fitness sharing encourages the formation of different feature detectors (hidden nodes) in the population. The number of hidden nodes in each hidden layer can vary.

One limitation of this approach [236] is that it could only deal with strictly layered feedforward ANN's. Another limitation is that there are usually several hidden nodes in the same species which have very similar functionality, i.e., which are basically the same feature detector in a population. Such redundancy needs to be removed by an additional clean-up algorithm.

Smith and Cribbs [181], [237] also used an individual to represent a hidden node rather than the whole ANN. Their approach can only deal with strictly three-layered feedforward ANN's.

C. The Evolution of Node Transfer Functions

The discussion on the evolution of architectures so far only deals with the topological structure of an architecture. The transfer function of each node in the architecture has been assumed to be fixed and predefined by human experts, yet the transfer function has been shown to be an important part of an ANN architecture and have significant impact on ANN's performance [238]–[240]. The transfer function is often assumed to be the same for all the nodes in an ANN, at least for all the nodes in the same layer.

Stork et al. [241] were, to our best knowledge, the first to apply EA's to the evolution of both topological structures and node transfer functions even though only simple ANN's with seven nodes were considered. The transfer function was specified in the structural genes in their genotypic representation. It was much more complex than the usual sigmoid function because they tried to model a biological neuron in the tailflip circuitry of crayfish.

White and Ligomenides [171] adopted a simpler approach to the evolution of both topological structures and node transfer functions. For each individual (i.e., ANN) in the initial population, 80% nodes in the ANN used the sigmoid transfer function and 20% nodes used the Gaussian transfer function. The evolution was used to decide the optimal mixture between these two transfer functions automatically. The sigmoid and Gaussian transfer function themselves were not evolvable. No parameters of the two functions were evolved.

Liu and Yao [191] used EP to evolve ANN's with both sigmoidal and Gaussian nodes. Rather than fixing the total number of nodes and evolve mixture of different nodes, their algorithm allowed growth and shrinking of the whole ANN by adding or deleting a node (either sigmoidal or Gaussian). The type of node added or deleted was determined at random. Good performance was reported for some benchmark problems [191]. Hwang et al. [225] went one step further. They evolved ANN topology, node transfer function, as well as connection weights for projection neural networks.

Sebald and Chellapilla [242] used the evolution of node transfer function as an example to show the importance of evolving representations. Representation and search are the two key issues in problem solving. Co-evolving solutions and their representations may be an effective way to tackle some difficult problems where little human expertise is available.

D. Simultaneous Evolution of Architectures and Connection Weights

The evolutionary approaches discussed so far in designing ANN architectures evolve architectures only, without any connection weights. Connection weights have to be learned after a near-optimal architecture is found. This is especially true if one uses the indirect encoding scheme, such as the developmental rule method. One major problem with the evolution of architectures without connection weights is noisy fitness evaluation [194]. In other words, fitness evaluation as described in step 3 of Fig. 6 is very inaccurate and noisy because a phenotype's (i.e., an ANN with a full set of weights) fitness was used to approximate its genotype's (i.e., an ANN without any weight information) fitness. There are two major sources of noise [194].

• The first source is the random initialization of the weights. Different random initial weights may produce different training results. Hence, the same genotype may have quite different fitness due to different random initial weights used in training.
• 2) The second source is the training algorithm. Different training algorithms may produce different training results even from the same set of initial weights. This is especially true for multimodal error functions. For example, BP may reduce an ANN's error to 0.05 through training, but an EA could reduce the error to 0.001 due to its global search capability.

Such noise may mislead evolution because the fact that the fitness of a phenotype generated from genotype $G_1$ is higher than that generated from genotype $G_2$ does not mean that $G_1$ truly has higher quality than $G_2$ . In order to reduce such noise, an architecture usually has to be trained many times from different random initial weights. The average result is then used to estimate the genotype's mean fitness. This method increases the computation time for fitness evaluation dramatically. It is one of the major reasons why only small ANN's were evolved in previous studies.

In essence, the noise identified in this paper is caused by the one-to-many mapping from genotypes to phenotypes. Angeline et al. [149] and Fogel [12], [243] have provided a more general discussion on the mapping between genotypes and phenotypes. It is clear that the evolution of architectures without any weight information has difficulties in evaluating fitness accurately. As a result, the evolution would be very inefficient.

One way to alleviate this problem is to evolve ANN architectures and connection weights simultaneously [37], [42], [45], [149], [165], [166], [169]–[172], [179], [180],

[182], [185]–[200], [230], [232]. In this case, each individual in a population is a fully specified ANN with complete weight information. Since there is a one-to-one mapping between a genotype and its phenotype, fitness evaluation is accurate.

One issue in evolving ANN's is the choice of search operators used in EA's. Both crossover-based and mutation-based EA's have been used. However, use of crossover appears to contradict the basic ideas behind ANN's, because crossover works best when there exist "building blocks" but it is unclear what a building block might be in an ANN since ANN's emphasize distributed (knowledge) representation [244]. The knowledge in an ANN is distributed among all the weights in the ANN. Recombining one part of an ANN with another part of another ANN is likely to destroy both ANN's.

However, if ANN's do not use a distributed representation but rather a localized one, such as radial basis function (RBF) networks or nearest-neighbor multilayer perceptrons, crossover might be a very useful operator. There has been some work in this area where good results were reported [119], [120], [245]–[253]. In general, ANN's using distributed representation are more compact and have better generalization capability for most practical problems.

Yao and Liu [193], [194] developed an automatic system, EPNet, based on EP for simultaneous evolution of ANN architectures and connection weights. EPNet does not use any crossover operators for the reason given above. It relies on a number of mutation operators to modify architectures and weights. Behavioral (i.e., functional) evolution, rather genetic evolution, is emphasized in EPNet. A number of techniques were adopted to maintain the behavioral link between a parent and its offspring [190]. Fig. 11 shows the main structure of EPNet.

EPNet uses rank-based selection [125] and five mutations: hybrid training; node deletion; connection deletion; connection addition; and node addition [188], [194], [254]. Hybrid training is the only mutation in EPNet which modifies ANN's weights. It is based on a modified BP (MBP) algorithm with an adaptive learning rate and simulated annealing. The other four mutations are used to grow and prune hidden nodes and connections.

The number of epochs used by MBP to train each ANN's in a population is defined by two user-specified parameters. There is no guarantee that an ANN will converge to even a local optimum after those epochs. Hence this training process is called partial training. It is used to bridge the behavioral gap between a parent and its offspring.

The five mutations are attempted sequentially. If one mutation leads to a better offspring, it is regarded as successful. No further mutation will be applied. Otherwise the next mutation is attempted. The motivation behind ordering mutations is to encourage the evolution of compact ANN's without sacrificing generalization. A validation set is used in EPNet to measure the fitness of an individual.

EPNet has been tested extensively on a number of benchmark problems and achieved excellent results, including parity problems of size from four to eight, the two-spiral

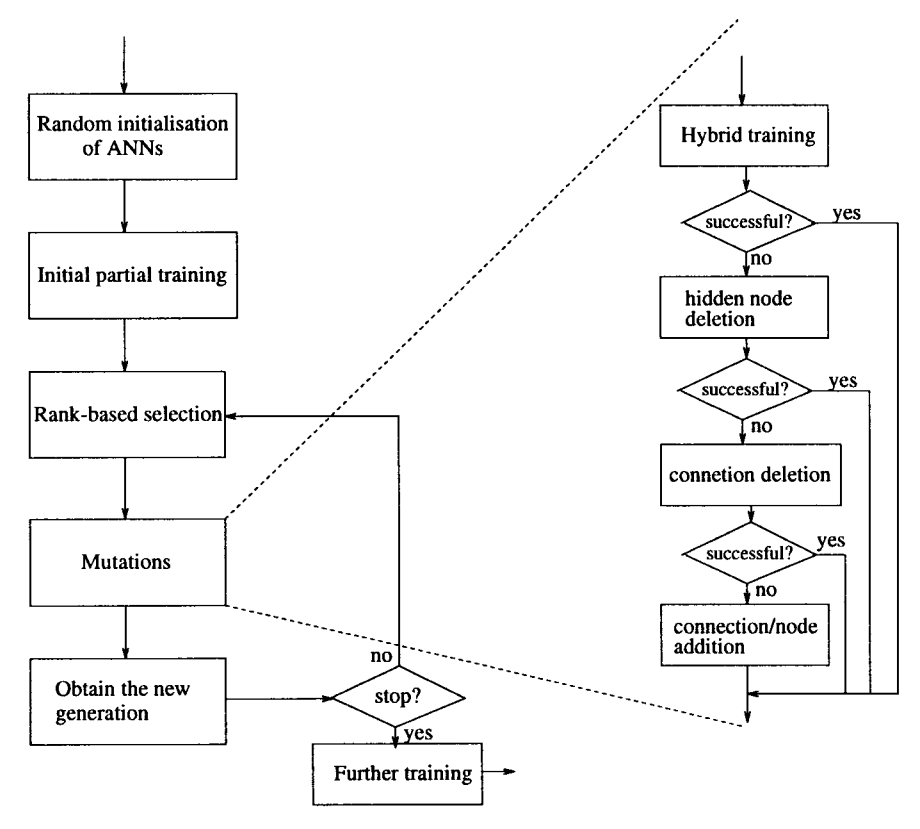
Fig. 11. The main structure of EPNet.

problem, the breast cancer problem, the diabetes problem, the heart disease problem, the thyroid problem, the Australian credit card problem, the Mackey–Glass time series prediction problem, etc. Very compact ANN's with good generalization ability have been evolved [185]–[195]. There are some other different EP-based systems for designing ANN's [128], [129], [217], [223], but none has been tested on as many different benchmark problems.

IV. THE EVOLUTION OF LEARNING RULES

An ANN training algorithm may have different performance when applied to different architectures. The design of training algorithms, more fundamentally the learning rules used to adjust connection weights, depends on the type of architectures under investigation. Different variants of the Hebbian learning rule have been proposed to deal with different architectures. However, designing an optimal learning rule becomes very difficult when there is little prior knowledge about the ANN's architecture, which is often the case in practice. It is desirable to develop an automatic and systematic way to adapt the learning rule to an architecture and the task to be performed. Designing a learning rule manually often implies that some assumptions, which are not necessarily true in practice, have to be made. For example, the widely accepted Hebbian learning rule has recently been shown to be outperformed by a new rule proposed by Artola et al. [255] in many cases [256]. The new rule can learn more patterns than the optimal Hebbian rule and can learn exceptions as well as regularities. It is, however, still difficult to say that this rule is optimal for

all ANN's. In fact, what is needed from an ANN is its ability to adjust its learning rule adaptively according to its architecture and the task to be performed. In other words, an ANN should learn its learning rule dynamically rather than have it designed and fixed manually. Since evolution is one of the most fundamental forms of adaptation, it is not surprising that the evolution of learning rules has been introduced into ANN's in order to learn their learning rules.

The relationship between evolution and learning is extremely complex. Various models have been proposed [257]-[271], but most of them deal with the issue of how learning can guide evolution [257]-[260] and the relationship between the evolution of architectures and that of connection weights [261]-[263]. Research into the evolution of learning rules is still in its early stages [264]-[267], [269], [270]. This research is important not only in providing an automatic way of optimizing learning rules and in modeling the relationship between learning and evolution, but also in modeling the creative process since newly evolved learning rules can deal with a complex and dynamic environment. This research will help us to understand better how creativity can emerge in artificial systems, like ANN's, and how to model the creative process in biological systems. A typical cycle of the evolution of learning rules can be described by Fig. 12. The iteration stops when the population converges or a predefined maximum number of iterations has been reached.

Similar to the reason explained in Section III-D, the fitness evaluation of each individual, i.e., the encoded learning rule, is very noisy because we use phenotype's

• 1. Decode each individual in the current generation into a learning rule.
• 1. Construct a set of ANNs with randomly generated architectures and initial connection weights, and train them using the decoded learning rule.
• 1. Calculate the fitness of each individual (encoded learning rule) according to the average training result.
• 1. Select parents from the current generation according to their fitness.
• 1. Apply search operators to parents to generate offspring which form the new generation.

Fig. 12. A typical cycle of the evolution of learning rules.

fitness (i.e., an ANN's training result) to approximate genotype's fitness (i.e., a learning rule's fitness). Such approximation may be inaccurate. Some techniques have been used to alleviate this problem, e.g., using a weighted average of the training results from ANN's with different initial connection weights in the fitness function. If the ANN architecture is predefined and fixed, the evolved learning rule would be optimized toward this architecture. If a near-optimal learning rule for different ANN architectures is to be evolved, the fitness evaluation should be based on the average training result from different ANN architectures in order to avoid overfitting a particular architecture.

A. The Evolution of Algorithmic Parameters

The adaptive adjustment of BP parameters (such as the learning rate and momentum) through evolution could be considered as the first attempt of the evolution of learning rules [32], [152], [272]. Harp et al. [152] encoded BP's parameters in chromosomes together with ANN's architecture. This evolutionary approach is different from the nonevolutionary one such as offered by Jacobs [273] because the simultaneous evolution of both algorithmic parameters and architectures facilitates exploration of interactions between the learning algorithm and architectures such that a near-optimal combination of BP with an architecture can be found.

Other researchers [32], [139], [213], [272] also used an evolutionary process to find parameters for BP but ANN's architecture was predefined. The parameters evolved in this case tend to be optimized toward the architecture rather than being generally applicable to learning. There are a number of BP algorithms with an adaptive learning rate and momentum where a nonevolutionary approach is used. Further comparison between the two approaches would be quite useful.

B. The Evolution of Learning Rules

The evolution of algorithmic parameters is certainly interesting but it hardly touches the fundamental part of a training algorithm, i.e., its learning rule or weight updating rule. Adapting a learning rule through evolution is expected to enhance ANN's adaptivity greatly in a dynamic environment.

Unlike the evolution of connection weights and architectures which only deal with static objects in an ANN, i.e., weights and architectures, the evolution of learning rules has to work on the dynamic behavior of an ANN. The key issue here is how to encode the dynamic behavior of a learning rule into static chromosomes. Trying to develop a universal representation scheme which can specify any kind of dynamic behaviors is clearly impractical, let alone the prohibitive long computation time required to search such a learning rule space. Constraints have to be set on the type of dynamic behaviors, i.e., the basic form of learning rules being evolved in order to reduce the representation complexity and the search space.

Two basic assumptions which have often been made on learning rules are: 1) weight updating depends only on local information such as the activation of the input node, the activation of the output node, the current connection weight, etc., and 2) the learning rule is the same for all connections in an ANN. A learning rule is assumed to be a linear function of these local variables and their products. That is, a learning rule can be described by the function [5]

$$\Delta w(t) = \sum_{k=1}^{n} \sum_{i_1, i_2, \dots, i_k=1}^{n} \left( \theta_{i_1 i_2 \dots i_k} \prod_{j=1}^{k} x_{i_j} (t-1) \right) \tag{4} $$

where t is time, $\Delta w$ is the weight change, $x_1, x_2, \ldots, x_n$ are local variables, and the $\theta$ 's are real-valued coefficients which will be determined by evolution. In other words, the evolution of learning rules in this case is equivalent to the evolution of real-valued vectors of $\theta$ 's. Different $\theta$ 's determine different learning rules. Due to a large number of possible terms in (4), which would make evolution very slow and impractical, only a few terms have been used in practice according to some biological or heuristic knowledge.

There are three major issues involved in the evolution of learning rules: 1) determination of a subset of terms described in (4); 2) representation of their real-valued coefficients as chromosomes; and 3) the EA used to evolve these chromosomes. Chalmers [264] defined a learning rule as a linear combination of four local variables and their six pairwise products. No third- or fourth-order^{3} terms

^<sup>3The order is defined as the number of variables in a product.

were used. Ten coefficients and a scale parameter were encoded in a binary string via exponential encoding. The architecture used in the fitness evaluation was fixed because only single-layer ANN's were considered and the number of inputs and outputs were fixed by the learning task at hand. After 1000 generations, starting from a population of randomly generated learning rules, the evolution discovered the well-known delta rule [7], [274] and some of its variants. These experiments, although simple and preliminary, demonstrated the potential of evolution in discovering novel learning rules from a set of randomly generated rules. However, constraints set on learning rules could prevent some from being evolved such as those which include third-or fourth-order terms.

Similar experiments on the evolution of learning rules were also carried out by others [265], [266], [267], [269], [270]. Fontanari and Meir [267] used Chalmers' approach to evolve learning rules for binary perceptrons. They also considered four local variables but only seven terms were adopted in their learning rules, which included one firstorder, three second-order, and three third-order terms in (4). Baxter [269] took one step further than just the evolution of learning rules. He tried to evolve complete ANN's (including connection weights, architectures, and learning rules) in a single level of evolution. It is clear that the search space of possible ANN's would be enormous if constraints were not set on the connection weights, architectures, and learning rules. In his experiments, only ANN's with binary threshold nodes were considered, so the weights could only be +1 or -1. The number of nodes in ANN's was fixed. The learning rule only considered two Boolean variables. Although Baxter's experiments were rather simple, they confirmed that complex behaviors could be learned and the ANN's learning ability could be improved through evolution [269].

Bengio et al.'s approach [265], [266] is slightly different from Chalmers' in the sense that gradient descent algorithms and simulated annealing, rather than EA's, were used to find near-optimal $\theta$ 's. In their experiments, four local variables and one zeroth-order, three first-order, and three second-order terms in (4) were used.

Research related to the evolution of learning rules includes Parisi et al.'s work on "econets," although they did not evolve learning rules explicitly [260], [275]. They emphasized the crucial role of the environment in which the evolution occured while only using some simple neural networks. The issue of environmental diversity is closely related to the noisy fitness evaluation as pointed out in Section III-D and at the beginning of Section IV. There are two possible sources of noise. The first is the decoding process (morphogenesis) of chromosomes. The second is introduced when a decoded learning rule is evaluated by using it to train ANN's. The environmental diversity is essential in obtaining a good approximation to the fitness of the decoded learning rule and thus in reducing the noise from the second source. If a general learning rule which is applicable to a wide range of ANN architectures and learning tasks is needed, the environmental diversity has to be very high, i.e., many different architectures and learning tasks have to be used in the fitness evaluation.

V. OTHER COMBINATIONS BETWEEN ANN'S AND EA'S

A. The Evolution of Input Features

For many practical problems, the possible inputs to an ANN can be quite large. There may be some redundancy among different inputs. A large number of inputs to an ANN increase its size and thus require more training data and longer training times in order to achieve a reasonable generalization ability. Preprocessing is often needed to reduce the number of inputs to an ANN. Various dimension reduction techniques, including the principal component analysis, have been used for this purpose.

The problem of finding a near-optimal set of input features to an ANN can be formulated as a search problem. Given a large set of potential inputs, we want to find a nearoptimal subset which has the fewest number of features but the performance of the ANN using this subset is no worse than that of the ANN using the whole input set. EA's have been used to perform such a search effectively [267], [277]–[287]. Very good results, i.e., better performance with fewer inputs, have been reported from these studies. In the evolution of input features, each individual in the population represents a subset of all possible inputs. This can be implemented using a binary chromosome whose length is the same as the total number of input features. Each bit in the chromosome corresponds to a feature. "1" indicates presence of a feature, while "0" indicates absence of the feature. The evaluation of an individual is carried out by training an ANN with these inputs and using the result to calculate its fitness value. The ANN architecture is often fixed. Such evaluation is very noisy, however, because of the reason explained in Section III-D.

Not only does the evolution of input features provide a way to discover important features from all possible inputs automatically, it can also be used to discover new training examples. Zhang and Veenker [288] described an active learning paradigm where a training algorithm based on EA's can self-select training examples. Cho and Cha [289] proposed another algorithm for evolving training sets by adding virtual samples.

B. ANN as Fitness Estimator

EA's have been used with success to optimize various control parameters [290]–[292]. However, it is very time consuming and costly to obtain fitness values for some control problems as it is impractical to run a real system for each combination of control parameters. In order to get around this problem and make evolution more efficient, fitness values are often approximated rather than computed exactly. ANN's are often used to model and approximate a real control system due to their good generalization abilities. The input to such ANN's will be a set of control parameters. The output will be the control system output from which an evaluation of the whole system can easily be

obtained. When an EA is used to search for a near-optimal set of control parameters, the ANN will be used in fitness evaluation rather than the real control system [293]–[297].

This combination of ANN's and EA's has a couple of advantages in evolving control systems. First, the time-consuming fitness evaluation based on real control systems is replaced by fast fitness evaluation based on ANN's. Second, this combination provides safer evolution of control systems. EA's are stochastic algorithms. It is possible that some poor control parameters may be generated in the evolutionary process. These parameters could damage a real control system. If we use ANN's to estimate fitness, we do not need to use the real system and thus can avoid damages to the real system. However, how successful this combination approach will be depends largely on how well ANN's learn and generalize.

C. Evolving ANN Ensembles

Learning is often formulated as an optimization problem in the machine learning field. However, learning is different from optimization in practice because we want the learned system to have best generalization, which is different from minimizing an error function on a training data set. The ANN with the minimum error on a training data set may not have best generalization unless there is an equivalence between generalization and the error on the training data. Unfortunately, measuring generalization quantitatively and accurately is almost impossible in practice [298] although there are many theories and criteria on generalization, such as the minimum description length (MDL) [299], Akaike information criteria (AIC) [300], and minimum message length (MML) [301]. In practice, these criteria are often used to define better error functions in the hope that minimizing the functions will maximize generalization. While these functions often lead to better generalization of learned systems, there is no guarantee.

EA's are often used to maximize a fitness function or minimize an error function, and thus they face the same problem as described above: maximizing a fitness function is different from maximizing generalization. The EA is actually used as an optimization, not learning, algorithm. While little can be done for traditional nonpopulation-based learning, there are opportunities for improving population-based learning, e.g., evolutionary learning.

Since the maximum fitness may not be equivalent to best generalization in evolutionary learning, the best individual with the maximum fitness in a population may not be the one we want. Other individuals in the population may contain some useful information that will help to improve generalization of learned systems. It is thus beneficial to make use of the whole population rather than any single individual. A population always contains at least as much information as any single individual. Hence, combining different individuals in the population to form an integrated system is expected to produce better results. Such a population of ANN's is called an ANN ensemble in this section. There have been some very successful

experiments which show that EA's can be used to evolve ANN ensembles [192], [193], [302]–[305].

D. Others

There are some other novel combinations between ANN's and EA's. For example, Zitar and Hassoun [306] used EA's to extract rules in a reinforcement learning system and then used them to train ANN's. Sziranyi [99] and Pal and Bhandari [98] used EA's to tune circuit parameters and templates in cellular ANN's. Olmez [97] used EA's to optimize a modified restricted Coulomb energy (RCE) ANN. Imada and Araki [307] used EA's to evolve connection weights for Hopfield ANN's. Many others used EA's and ANN's for combinatorial or global (numerical) optimization in order to combine EA's global search capability with ANN's fast convergence to local optima [308]–[318].

VI. CONCLUDING REMARKS

Although evolution has been introduced into ANN's at various levels, they can roughly be divided into three: the evolution of connection weights, architectures, and learning rules. This section first describes a general framework for ANN's and then draws some conclusions.

A. A General Framework for EANN's

A general framework for EANN's can be described by Fig. 13 [3]–[5]. The evolution of connection weights proceeds at the lowest level on the fastest time scale in an environment determined by an architecture, a learning rule, and learning tasks. There are, however, two alternatives to decide the level of the evolution of architectures and that of learning rules: either the evolution of architectures is at the highest level and that of learning rules at the lower level or vice versa. The lower the level of evolution, the faster the time scale it is on.

From the engineering perspective, the decision on the level of evolution depends on what kind of prior knowledge is available. If there is more prior knowledge about an ANN's architecture than that about their learning rules, or if a particular class of architectures is pursued, it is better to put the evolution of architectures at the highest level because such knowledge can be encoded in an architecture's genotypic representation to reduce the (architecture) search space and the lower-level evolution of learning rules can be biased toward this type of architectures. On the other hand, the evolution of learning rules should be at the highest level if there is more prior knowledge about them available or if there is a special interest in certain type of learning rules. Unfortunately, there is usually little prior knowledge available about either architectures or learning rules in practice except for some very vague statements [319]. In this case, it is more appropriate to put the evolution of architectures at the highest level since the optimality of a learning rule makes more sense when evaluated in an environment including the architecture to which the

Fig. 13. A general framework for EANN's.

learning rule is applied. Fig. 13 summarizes different levels of evolution in ANN's.

Fig. 13 can also be viewed as a general framework of adaptive systems if we do not restrict ourselves to EA's and three levels. Simulated annealing, gradient descent, and even exhaustive search could be considered as special cases of EA's. For example, the traditional BP network can be considered as a special case of our general framework with one-shot (only-one-candidate) search used in the evolution of architectures and learning rules and BP used in the evolution of connection weights. In fact, the general framework provides a basis for comparing various specific EANN models according to the search procedures they used at three different levels since it defines a three-dimensional space where zero represents one-shot search and $+\infty$ represents exhaustive search along each axis. Each EANN model corresponds to a point in this space.

B. Conclusions

Evolution can be introduced into ANN's at many different levels. The evolution of connection weights provides a global approach to connection weight training, especially when gradient information of the error function is difficult or costly to obtain. Due to the simplicity and generality of the evolution and the fact that gradient-based training algorithms often have to be run multiple times in order to avoid being trapped in a poor local optimum, the evolutionary approach is quite competitive.

Evolution can be used to find a near-optimal ANN architecture automatically. This has several advantages over heuristic methods of architecture design because of the

characteristics of the design problem given in the beginning of Section III. The direct encoding scheme of ANN architectures is very good at fine tuning and generating a compact architecture. The indirect encoding scheme is suitable for finding a particular type of ANN architecture quickly. Separating the evolution of architectures and that of connection weights can make fitness evaluation inaccurate and mislead evolution. Simultaneous evolution of ANN architectures and connection weights generally produces better results. It is argued that crossover produces more harm than benefit in evolving ANN's using distributed representation (e.g., multilayer perceptrons) because it destroys knowledge learned and distributed among different connections easily. Crossover would be more suitable for localized ANN's, such as RBF networks.

Evolution can also be used to allow an ANN to adapt its learning rule to its environment. In a sense, the evolution provides ANN's with the ability of learning to learn. It also helps to model the relationship between learning and evolution. Preliminary experiments have shown that efficient learning rules can be evolved from randomly generated rules. Current research on the evolution of learning rules normally assumes that learning rules can be specified by (4). While constraints on learning rules are necessary to reduce the search space in the evolution, they might prevent some interesting learning rules from being discovered.

Global search procedures such as EA's are usually computationally expensive. It would be better not to employ EA's at all three levels of evolution. It is, however, beneficial to introduce global search at some levels of evolution, especially when there is little prior knowledge available at that level and the performance of the ANN is required to be high, because the trial-and-error and other heuristic methods are very ineffective in such circumstances.

With the increasing power of parallel computers, the evolution of large ANN's becomes feasible. Not only can such evolution discover possible new ANN architectures and learning rules, but it also offers a way to model the creative process as a result of ANN's adaptation to a dynamic environment.

ACKNOWLEDGMENT

The author is grateful to D. B. Fogel and an anonymous referee for their constructive comment on earlier versions of this paper.

REFERENCES

• [1] X. Yao, "Evolution of connectionist networks," in Preprints Int. Symp. AI, Reasoning & Creativity, Queensland, Australia, Griffith Univ., 1991, pp. 49–52.
• Griffith Univ., 1991, pp. 49–52.
  [2] _____, "A review of evolutionary artificial neural networks," Int. J. Intell. Syst., vol. 8, no. 4, pp. 539–567, 1993.
• J. Intell. Syst., vol. 8, no. 4, pp. 539–567, 1993.
  [3] _____, "Evolutionary artificial neural networks," Int. J. Neural Syst., vol. 4, no. 3, pp. 203–222, 1993.
• Syst., vol. 4, no. 3, pp. 203–222, 1993.

[4] _____, "The evolution of connectionist networks," in Artificial Intelligence and Creativity, T. Dartnall, Ed. Dordrecht, The Netherlands: Kluwer, pp. 233–243, 1994.
- [5] _____, "Evolutionary artificial neural networks," in Encyclopedia of Computer Science and Technology, vol. 33, A. Kent and J. G. Williams, Eds. New York: Marcel Dekker, 1995, pp. 137–170.

• [6] G. E. Hinton, "Connectionist learning procedures," Artificial Intell., vol. 40, no. 1–3, pp. 185–234, Sept. 1989.
  [7] J. Hertz, A. Krogh, and R. Palmer, Introduction to the Theory of
• Veural Computation. Reading, MA: Addison-Wesley, 1991.
• [8] H.-P. Schwefel, Numerical Optimization of Computer Models. Chichester, U.K.: Wiley, 1981.
• H.-P. Schwefel, Evolution and Optimum Seeking. New York: Wiley, 1995.
• [10] L. J. Fogel, A. J. Owens, and M. J. Walsh, Artificial Intelligence Through Simulated Evolution. New York: Wiley, 1966.
• [11] D. B. Fogel, System Identification Through Simulated Evolution: A Machine Learning Approach to Modeling. Needham Heights, MA: Ginn, 1991.
• , Evolutionary Computation: Toward a New Philosophy of Machine Intelligence. New York: IEEE Press, 1995
• [13] J. H. Holland, Adaptation in Natural and Artificial Systems. Ann Arbor, MI: Univ. Michigan Press, 1975.
• [14] D. E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning. Reading, MA: Addison-Wesley, 1989.
• [15] D. B. Fogel, "An introduction to simulated evolutionary optimization," IEEE Trans. Neural Networks, vol. 5, pp. 3-14, Jan.
• [16] T. Bäck, U. Hammel, and H.-P. Schwefel, "Evolutionary computation: Comments on the history and current state," IEEE Trans. Evolutionary Computation, vol. 1, pp. 3-17, Apr. 1997.
• [17] D. R. Hush and B. G. Horne, "Progress in supervised neural networks," IEEE Signal Processing Mag., vol. 10, pp. 8-39, Jan. 1993.
• [18] D. E. Rumelhart, G. E. Hinton, and R. J. Williams, "Learning internal representations by error propagation," in Parallel Distributed Processing: Explorations in the Microstructures of Cognition, vol. I, D. E. Rumelhart and J. L. McClelland, Eds.
• Cambridge, MA: MIT Press, 1986, pp. 318–362. [19] M. F. Møller, "A scaled conjugate gradient algorithm for fast supervised learning," Neural Networks, vol. 6, no. 4, pp. 525-533, 1993.
• [20] K. J. Lang, A. H. Waibel, and G. E. Hinton, "A time-delay neural network architecture for isolated word recognition,
• Neural Networks, vol. 3, no. 1, pp. 33–43, 1990.
  [21] S. S. Fels and G. E. Hinton, "Glove-talk: A neural network interface between a data-glove and a speech synthesizer," IEEE Trans. Neural Networks, vol. 4, pp. 2-8, Jan. 1993.
• [22] S. Knerr, L. Personnaz, and G. Dreyfus, "Handwritten digit recognition by neural networks with single-layer training, IEEE Trans. Neural Networks, vol. 3, pp. 962-968, Nov. 1992.
• [23] R. S. Sutton, "Two problems with backpropagation and other steepest-descent learning procedures for networks," in Proc. 8th Annual Conf. Cognitive Science Society. Hillsdale, NJ:
• Erlbaum, 1986, pp. 823–831. [24] D. Whitley, T. Starkweather, and C. Bogart, "Genetic algorithms and neural networks: Optimizing connections and connectivity," Parallel Comput., vol. 14, no. 3, pp. 347-361,
• [25] Y. Chauvin and D. E. Rumelhart, Eds., Backpropagation: Theory, Architectures, and Applications. Hillsdale, NJ: Erlbaum, 1995.
• [26] D. Whitley, "The GENITOR algorithm and selective pressure: Why rank-based allocation of reproductive trials is best," in Proc. 3rd Int. Conf. Genetic Algorithms and Their Applications, J. D. Schaffer, Ed. San Mateo, CA: Morgan Kaufmann, 1989, pp. 116–121.
• [27] D. Montana and L. Davis, "Training feedforward neural networks using genetic algorithms," in Proc. 11th Int. Joint Conf. Artificial Intelligence. San Mateo, CA: Morgan Kaufmann,
• 1989, pp. 762–767. [28] T. P. Caudell and C. P. Dolan, "Parametric connectivity: Training of constrained networks using genetic algorithms," in Proc. 3rd Int. Conf. Genetic Algorithms and Their Applications, J. D. Schaffer, Ed. San Mateo, CA: Morgan Kaufmann, 1989, p. 370-374.
• [29] D. B. Fogel, L. J. Fogel, and V. W. Porto, "Evolving neural networks," Biological Cybern., vol. 63, no. 6, pp. 487-493,
• [30] P. Bartlett and T. Downs, "Training a neural network with a genetic algorithm," Dep. Elect. Eng., Univ. Queensland, Australia, Tech. Rep., Jan. 1990.

• [31] J. Heistermann and H. Eckardt, "Parallel algorithms for learning in neural networks with evolution strategy," in Proc. Parallel

• Computing'89, D. J. Evans, G. R. Joubert, and F. J. Peters, Eds. Amsterdam, The Netherlands: Elsevier, 1989, pp. 275-280.

• [32] R. K. Belew, J. McInerney, and N. N. Schraudolph, "Evolving networks: Using genetic algorithm with connectionist learning, Comput. Sci. Eng. Dep. (C-014), , Univ. of California, San
• Diego, Tech. Rep. CS90-174 (revised), Feb. 1991. [33] N. J. Radcliffe, "Genetic neural networks on MIMD computers (compressed edition)," Ph.D. dissertation, Dep. Theoretical Phys., Univ. Edinburgh, U.K., 1990.
• [34] D. L. Prados, "Training multilayered neural networks by replacing the least fit hidden neurons," in Proc. IEEE SOUTHEAST-
• CON'92, vol. 2, pp. 634–637. [35] H. de Garis, "Steerable genNets: The genetic programming of steerable behaviors in genNets," in Toward a Practice of Autonomous Systems: Proc. 1st Europ. Conf. Artificial Life, F. J. Varela and P. Bourgine, Eds. Cambridge, MA: MIT Press, 1991, pp. 272–281.
• _, "Using the genetic algorithm to train time dependent behaviors in neural networks," in Proc. 1st Int. Workshop Multistrategy Learning (MSL-91), R. S. Michalski and G. Tecuci, Eds. Fairfax, VA: Center for Artificial Intelligence, 1991, pp. 273-280.
• [37] M. Srinivas and L. M. Patnaik, "Learning neural network weights using genetic algorithms—Improving performance by search-space reduction," in Proc. 1991 IEEE Int. Joint Conf. Neural Networks (IJCNN'91 Singapore), vol. 3, pp. 2331–2336.
• [38] H. de Garis, "GenNets: Genetically programmed neural nets—Using the genetic algorithm to train neural nets whose inputs and/or outputs vary in time," in Proc. 1991 IEEE Int. Joint Conf. Neural Networks (IJCNN'91 Singapore), vol. 2, pp. 1391-1396.
• [39] A. Homaifar and S. Guan, "Training weights of neural networks by genetic algorithms and messy genetic algorithms," in Proc. 2nd IASTED Int. Symp. Expert Systems and Neural Networks,
• M. H. Hamza, Ed. Anaheim, CA: Acta, 1990, pp. 74–77. [40] D. L. Prados, "New learning algorithm for training multilayered neural networks that uses genetic-algorithm techniques," Electron. Lett., vol. 28, pp. 1560-1561, July 1992.
• [41] A. P. Wieland, "Evolving neural network controllers for unstable systems," in Proc. 1991 IEEE Int. Joint Conf. Neural Networks (IJCNN'91 Seattle), vol. 2, pp. 667–673. [42] J. R. Koza and J. P. Rice, "Genetic generation of both the
• weights and architecture for a neural network," in Proc. 1991 IEEE Int. Joint Conf. Neural Networks (IJCNN'91 Seattle), vol. , pp. 397–404.
• [43] S. Dominic, R. Das, D. Whitley, and C. Anderson, "Genetic reinforcement learning for neural networks," in Proc. 1991 IEEE Int. Joint Conf. Neural Networks (IJCNN'91 Seattle), vol. 2, pp. 71–76.
• [44] F. A. Dill and B. C. Deer, "An exploration of genetic algorithms for the selection of connection weights in dynamical neural networks," in Proc. IEEE 1991 National Aerospace and Electronics
• Conf. NAECON 1991, vol. 3, pp. 1111–1115. [45] S. Bornholdt and D. Graudenz, "General asymmetric neural networks and structure design by genetic algorithms," Neural
• Networks, vol. 5, no. 2, pp. 327–334, 1992. [46] B. Maricic, "Genetically programmed neural network for solving pole-balancing problem," in Artificial Neural Networks: Proc. Int. Conf. Artificial Neural Networks—ICANN-91, vol. 2, T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, Eds. Amsterdam, The Netherlands: North-Holland, 1991,
• pp. 1273–1276.
  [47] J. J. Spofford and K. J. Hintz, "Evolving sequential machines in amorphous neural networks," in Artificial Neural Networks: Proc. Int. Conf. Artificial Neural Networks—ICANN-91, vol. 1, T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, Eds. Amsterdam, The Netherlands: North-Holland, 1991, pp. 973-978.
• [48] F. Menczer and D. Parisi, "Evidence of hyperplanes in the genetic learning of neural networks," Biological Cybern., vol. 66, pp. 283–289, 1992.
• [49] Y. Ichikawa and T. Sawa, "Neural network application for direct feedback controllers," IEEE Trans. Neural Networks, vol. 3, pp. 224-231, Mar. 1992.
• [50] A. W. O'Neil, "Genetic based training of two-layer, optoelectronic neural network," Electron. Lett., vol. 28, pp. 47–48, Jan.

• [51] J. Heistermann, "A mixed genetic approach to the optimization of neural controllers," in Proc. CompEuro '92, P. Dewilde and J.

• Vandewallele, Eds. Los Alamitos, CA: IEEE Computer Soc., 1992, pp. 459–464.

• [52] D. J. Janson and J. F. Frenzel, "Application of genetic algorithms to the training of higher order neural networks," J. Syst. Eng., vol. 2, pp. 272–276, 1992.
• [53] D. J. Janson and J. F. Frenzel, "Training product unit neural networks with genetic algorithms," IEEE Expert, vol. 8, pp. 26–33, May 1993.
• [54] A. V. Scherf and L. D. Voelz, "Training neural networks with genetic algorithms for target detection," in Proc. SPIE, Conf. Science of Artificial Neural Networks, vol. 1710, pt. 1, Orlando, FL, 1992, pp. 734–741.
• [55] E. DeRouin and J. Brown, "Alternative learning methods for training neural network classifiers," in Proc. SPIE, Conf. Science of Artificial Neural Networks, pt. 1, vol. 1710, Orlando, FL, 1992, pp. 474–483.
• [56] M. A. Lewis, A. H. Fagg, and A. Solidum, "Genetic programming approach to the construction of a neural network for control of a walking robot," in Proc. 1992 IEEE Int. Conf. Robotics and Automation, vol. 3. Los Alamitos, CA: IEEE Computer Soc., 1992, pp. 2618–2623.
• [57] H. B. Penfold, O. F. Diessel, and M. W. Bentink, "A genetic breeding algorithm which exhibits self-organizing in neural networks," in Proc. IASTED Int. Symp. Artificial Intelligence Application and Neural Networks—AINN'90, M. H. Hamza, Ed. Anaheim, CA: ACTA, 1990, pp. 293–296.
• [58] M. L. Gargano, R. A. Marose, and L. von Kleeck, "An application of artificial neural networks and genetic algorithms to personnel selection in the financial industry," in Proc. 1st Int. Conf. Artificial Intelligence on Wall Street. Los Alamitos, CA: IEEE Computer Soc., 1991, pp. 257–262.
• IEEE Computer Soc., 1991, pp. 257–262.
  [59] J. G. Elias, "Genetic generation of connection patterns for a dynamic artificial neural network," in Proc. Int. Workshop Combinations of Genetic Algorithms and Neural Networks (COGANN-92), D. Whitley and J. D. Schaffer, Eds. Los Alamitos, CA: IEEE Computer Soc., 1992, pp. 38–54.
• [60] R. D. Beer and J. C. Gallagher, "Evolving dynamical neural networks for adaptive behavior," Adaptive Behavior, vol. 1, no. 1, pp. 91–122, 1992.
• [61] L. Meeden, "Incremental approach to developing intelligent neural network controllers for robots," IEEE Trans. Syst., Man, Cybern. B, vol. 26, pp. 474–485, Mar. 1996.
• [62] S. Baluja, "Evolution of an artificial neural network based autonomous land vehicle controller," IEEE Trans. Syst., Man, Cybern. B, vol. 26, pp. 450–463, Mar. 1996.
• [63] V. W. Porto, D. B. Fogel, and L. J. Fogel, "Alternative neural network training methods," IEEE Expert, vol. 10, pp. 16–22, Mar. 1995.
• [64] S. Yao, C. J. Wei, and Z. Y. He, "Evolving wavelet neural networks for function approximation," Electron. Lett., vol. 32, no. 4, pp. 360–361, 1996.
• [65] G. W. Greenwood, "Training partially recurrent neural networks using evolutionary strategies," IEEE Trans. Speech Audio Processing, vol. 5, pp. 192–194. Feb. 1997.
• Processing, vol. 5, pp. 192–194, Feb. 1997.
  [66] A. Chilingarian, S. Ter-Antonyan, and A. Vardanyan, "Comparison of Bayesian and neural techniques in problems of classification to multiple categories," Nuclear Instrum. Methods in Phys. Res., Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 389, nos. 1–2, pp. 230–232, 1997
• [67] A. P. Topchy and O. A. Lebedko, "Neural network training by means of cooperative evolutionary search," Nuclear Instrum. Methods in Phys. Res., Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 389, nos. 1–2, pp. 240–241, 1997.
• [68] R. Berlich and M. Kunze, "Comparison between the performance of feed forward neural networks and the supervised growing neural gas algorithm," Nuclear Instrum. Methods in Phys. Res., Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 389, nos. 1–2, pp. 274–277, 1997
• [69] Y. Ikuno, H. Kawabata, Y. Hirao, M. Hirata, T. Nagahara, and Y. Inagaki, "Application of an improved genetic algorithm to the learning of neural networks," Solid State Commun., vol. 91, no. 3, pp. 731–735, 1994.

• [70] W. Kinnebrock, "Accelerating the standard backpropagation method using a genetic approach," Neurocomput., vol. 6, nos. 5–6, pp. 583–588, 1994.

• [71] S. L. Hung and H. Adeli, "Parallel genetic/neural network learning algorithm for MIMD shared memory machines," IEEE Trans. Neural Networks, vol. 5, pp. 900–909, Nov. 1994.

• Trans. Neural Networks, vol. 5, pp. 900–909, Nov. 1994.
  [72] T. Maifeld and G. Sheble, "Short-term load forecasting by a neural network and a refined genetic algorithm," Electric Power Syst. Res., vol. 31, no. 3, pp. 147–152, 1994.
• [73] B. Deo, A. Datta, B. Kukreja, R. Rastogi, and K. Deb, "Optimization of back propagation algorithm and GAS-assisted ANN models for hot metal desulphurization," Steel Res., vol. 65, no. 12, pp. 528–533, 1994.
• 12, pp. 528–533, 1994.
  [74] A. J. Skinner and J. Q. Broughton, "Neural networks in computational materials science: Training algorithms," Modeling and Simulation in Materials Sci. Eng., vol. 3, no. 3, pp. 371–390, 1995
• [75] Y. Chen, M. Narita, and T. Yamada, "Nuclear reactor diagnostic system using genetic algorithm (GA)-trained neural networks," Elect. Eng. Japan (English Translation of Denki Gakkai Ron-bunshi), vol. 115, no. 5, pp. 88–99, 1995.
• [76] M. Lehotsky, V. Olej, and J. Chmurny, "Pattern recognition based on the fuzzy neural networks and their learning by modified genetic algorithms," Neural Network World, vol. 5, no. 1, pp. 91–97, 1995.
• no. 1, pp. 91–97, 1995. [77] N. Wang, D. Yao, and F. Zhang, "Genetic-based fuzzy net controller and its application," Advances in Modeling and Anal. B, vol. 38, nos. 1–2, pp. 49–58, 1997.
• [78] P. Osmera, "Optimization of neural networks by genetic algorithms," Neural Network World, vol. 5, no. 6, pp. 965–976, 1995.
• [79] S. Jain, P.-Y. Peng, A. Tzes, and F. Khorrami, "Neural network design with genetic learning for control of a single link flexible manipulator," J. Intell. Robot. Syst.: Theory Applicat., vol. 15, no. 2, pp. 135–151, 1996.
• no. 2, pp. 135–151, 1996.
  [80] M. A. Taha and A. S. Hanna, "Evolutionary neural network model for the selection of pavement maintenance strategy,"

Transportation Res. Rec., vol. 1497, pp. 70–76. May 1995.
- Transportation Res. Rec., vol. 1497, pp. 70–76, May 1995.

[81] S.-W. Lee, "Off-line recognition of totally unconstrained handwritten numerals using multilayer cluster neural network," IEEE Trans. Pattern Anal. Machine Intell., vol. 18, pp. 648–652, June 1996
- [82] S.-K. Lee and D. Jang, "Translation, rotation and scale invariant pattern recognition using spectral analysis and hybrid geneticneural-fuzzy networks," Comput. Ind. Eng., vol. 30, no. 3, pp. 511–522, 1996.
- [83] J. V. Hansen and R. D. Meservy, "Learning experiments with genetic optimization of a generalized regression neural network," Decision Support Syst., vol. 18, nos. 3–4, pp. 317–325, 1996.
- [84] S.-J. Huang and C.-L. Huang, "Genetic-based multilayered perceptron for Taiwan power system short-term load forecasting," Electric Power Syst. Res., vol. 38, no. 1, pp. 69–74, 1996.
- [85] _____, "Application of genetic-based neural networks to thermal unit commitment," IEEE Trans. Power Syst., vol. 12, pp. 654–660, Feb. 1997.
- [86] Y. M. Chen and R. M. O'Connell, "Active power line conditioner with a neural network control," IEEE Trans. Ind. Applicat., vol. 33, pp. 1131–1136, July/Aug. 1997.
- Applicat., vol. 33, pp. 1131–1136, July/Aug. 1997.
[87] C. R. Chen and C. H. Chu, "Concurrent training algorithm for supervised learning in artificial neural networks," J. Inform. Sci. Eng., vol. 13, no. 2, pp. 267–291, 1997.
- [88] J. Jarmulak, P. Spronck, and E. J. H. Kerckhoffs, "Neural networks in process control: Model-based and reinforcement trained controllers," Comput. Electron. Agriculture, vol. 18, nos. 2–3, pp. 149–166, 1997.
- [89] R. S. Sexton, R. E. Dorsey, and J. D. Johnson, "Toward global optimization of neural networks: A comparison of the genetic algorithm and backpropagation," Decision Support Syst., vol. 22, no. 2, pp. 171–185, 1998.
- [90] M. Kamo, T. Kubo, and Y. Iwasa, "Neural network for female mate preference, trained by a genetic algorithm," Philosophical Trans. Roy. Soc., vol. 353, no. 1367, p. 399, 1998.
[91] J. Zhou and D. L. Civco, "Using genetic learning neural
- [91] J. Zhou and D. L. Civco, "Using genetic learning neural networks for spatial decision making in GIS," PE & RS: Photogrammetric Eng. Remote Sensing, vol. 62, no. 11, pp. 1287–1295, 1996.
- [92] B. Yoon, D. J. Holmes, and G. Langholz, "Efficient genetic algorithms for training layered feedforward neural networks," Inform. Sci., vol. 76, nos. 1–2, pp. 67–85, 1994.
- [93] P. G. Korning, "Training neural networks by means of genetic

• algorithms working on very long chromosomes," Int. J. Neural Syst., vol. 6, no. 3, pp. 299–316, 1995.
• [94] S. Park, L.-J. Park, and C. Park, "A neuro-genetic controller for nonminimum phase systems," IEEE Trans. Neural Networks, vol. 6, pp. 1297-1300, Sept. 1995.
• [95] D. B. Fogel, E. C. Wasson, and V. W. Porto, "A step toward computer-assisted mammography using evolutionary programming and neural networks," Cancer Lett., vol. 119, no. 1, p. 93, 1997.
• [96] D. B. Fogel, E. C. Wasson, and E. M. Boughton, "Evolving neural networks for detecting breast cancer," Cancer Lett., vol.
• 96, no. 1, pp. 49–53, 1995. [97] T. Olmez, "Classification of EEG waveforms by using RCE neural networks and genetic algorithms," Electron. Lett., vol. 33, no. 18, pp. 1561-1562, 1997.
• [98] S. Pal and D. Bhandari, "Genetic algorithms with fuzzy fitness function for object extraction using cellular networks," Fuzzy Sets and Syst., vol. 65, nos. 2-3, pp. 129-139, 1994.
• [99] T. Sziranyi, "Robustness of cellular neural networks in image deblurring and texture segmentation," Int. J. Circuit Theory
• Applicat., pt 2, vol. 24, no. 3, pp. 381–396, 1996.
  [100] P. Adamidis and V. Petridis, "Co-operating populations with different evolution behaviors," in Proc. 1996 IEEE Int. Conf. Evolutionary Computation, ICEC'96, pp. 188-191.
• [101] D. Thierens, "Non-redundant genetic coding of neural networks," in Proc. 1996 IEEE Int. Conf. Evolutionary Compu-
• tation, ICEC'96, pp. 571–575.
  [102] R. G. Hutchins, "Identifying nonlinear dynamic systems using neural nets and evolutionary programming," in Proc. 28th Asilomar Conf. Signals, Systems & Computers. Part 2 (of 2). Los Alamitos, CA: IEEE Computer Soc., 1994, pp. 887–891. [103] J. Lei, G. He, and J.-P. Jiang, "State estimation of the CSTR
• system based on a recurrent neural network trained by HGA's,' in Proc. 1997 IEEE Int. Conf. Neural Networks. Part 2 (of 4), pp. 779-782.
• [104] D. Popvic and K. C. S. Murty, "Retaining diversity of search point distribution through a breeder genetic algorithm for neural network learning," in Proc. 1997 IEEE Int. Conf. Neural Networks. Part 1 (of 4), pp. 495–498.
• [105] A. Likartsis, I. Vlachavas, and L. H. Tsoukalas, "New hybrid neural-genetic methodology for improving learning," in Proc. 9th IEEE Int. Conf. Tools with Artificial Intelligence, pp. 32–36.
• [106] A. Schultz and H. Wechsler, "Data fusion in neural networks via computational evolution," in Proc. 1994 IEEE Int. Conf. Neural Networks. Part 5 (of 7), pp. 3044–3049.
  [107] M. Koeppen, M. Teunis, and B. Nickolay, "Neural network
• that uses evolutionary learning," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation, ICEC'97, pp. 635–639.
• [108] J. Aguilar and A. Colmenares, "Recognition algorithm using evolutionary learning on the random neural networks," in Proc. 1997 IEEE Int. Conf. Neural Networks. Part 2 (of 4), pp. 1023-1028.
• [109] R. Hochman, T. M. Khoshgoftaar, E. B. Allen, and J. P. Hudepohl, "Evolutionary neural networks: A robust approach to software reliability problems," in Proc. 1997 8th Int. Symp. Software Reliability Engineering. Los Alamitos, CA: IEEE
• Computer Soc., 1997, pp. 13–26. [110] W. Yan, Z. Zhu, and R. Hu, "Hybrid genetic/BP algorithm and its application for radar target classification," in Proc. 1997 IEEE National Aerospace and Electronics Conf., NAECON. Part 2 (of 2), pp. 981–984.
• [111] J.-M. Yang, C.-Y. Kao, and J.-T. Horng, "Evolving neural induction regular language using combined evolutionary algorithms," in Proc. 1996 1st Joint Conf. Intelligent Systems/ISAI/IFIS, pp. 162-169.
• [112] P. Zhang, Y. Sankai, and M. Ohta, "Hybrid adaptive learning control of nonlinear system," in Proc. 1995 American Control
• Conf. Part 4 (of 6), pp. 2744–2748.
  [113] P. J. B. Hancock, "Genetic algorithms and permutation problems: A comparison of recombination operators for neural net structure specification," in Proc. Int. Workshop Combinations of Genetic Algorithms and Neural Networks (COGANN-92), D. Whitley and J. D. Schaffer, Eds. Los Alamitos, CA: IEEE

• Computer Soc., 1992, pp. 108–122. [114] J. Antonisse, "A new interpretation of schema notation that overturns the binary encoding constraint," in Proc. 3rd Int. Conf. Genetic Algorithms and Their Applications, J. D. Schaffer, Ed. San Mateo, CA: Morgan Kaufmann, 1989, pp. 86-91.

• [115] N. J. Radcliffe, "Equivalence class analysis of genetic algo-

• rithms," Complex Syst., vol. 5, no. 2, pp. 183–205, 1991.
  [116] D. B. Fogel and A. Ghozeil, "A note on representations and variation operators," IEEE Trans. Evolutionary Computation, vol. 1, pp. 159-161, July 1997.
• [117] N. Saravanan and D. B. Fogel, "Evolving neural control systems," IEEE Expert, vol. 10, pp. 23-27, Mar. 1995.
• [118] K. S. Tang, C. Y. Chan, K. F. Man, and S. Kwong, "Genetic structure for NN topology and weights optimization," in Proc. 1st IEE/IEEE Int. Conf. Genetic Algorithms in Engineering Systems: Innovations and Applications (GALESIA'95), Stevenage,
• U.K., Inst. Elect. Eng. Conf. Pub. 414, pp. 250–255. [119] M. Sarkar and B. Yegnanarayana, "Evolutionary programmingbased probabilistic neural networks construction technique," in Proc. 1997 IEEE Int. Conf. Neural Networks, Part 1 (of 4), pp.
• [120] P. J. Angeline, "Evolving basis functions with dynamic receptive fields," in Proc. 1997 IEEE Int. Conf. Systems, Man, and
• Cybernetics, Part 5 (of 5), pp. 4109–4114. [121] X. Yao and Y. Liu, "Fast evolutionary programming," in Evolutionary Programming V: Proc. 5th Annu. Conf. Evolutionary Programming, L. J. Fogel, P. J. Angeline, and T. Bäck, Eds. Cambridge, MA: MIT Press, 1996, pp. 451-460.
• [122] X. Yao, G. Lin, and Y. Liu, "An analysis of evolutionary algorithms based on neighborhood and step sizes," in Evolutionary Programming VI: Proc. 6th Annu. Conf. Evolutionary Programming, vol. 1213 of Lecture Notes in Computer Science, P. J. Angeline, R. G. Reynolds, J. R. McDonnell, and R. Eberhart, Eds. Berlin, Germany: Springer-Verlag, 1997, pp. 297-307.
• [123] T. Bäck and H.-P. Schwefel, "An overview of evolutionary algorithms for parameter optimization," Evolutionary Computation, vol. 1, no. 1, pp. 1-23, 1993.
• [124] X. Yao and Y. Liu, "Fast evolution strategies," Control Cybern., vol. 26, no. 3, pp. 467-496, 1997.
• [125] X. Yao, "An empirical study of genetic operators in genetic algorithms," Microprocessing and Microprogramming, vol. 38,
• no. 1–5, pp. 707–714, Sept. 1993. [126] J. Torreele, "Temporal processing with recurrent networks: An evolutionary approach," in Proc. 4th Int. Conf. Genetic Algorithms, R. K. Belew and L. B. Booker, Eds. San Mateo, CA: Morgan Kaufmann, 1991, pp. 555-561.
• [127] M. Mandischer, "Evolving recurrent neural networks with nonbinary encoding," in Proc. 1995 IEEE Int. Conf. Evolutionary Computation, Part 2 (of 2), pp. 584-589.
• [128] F. Heimes, G. Zalesski, W. L. Jr., and M. Oshima, "Traditional and evolved dynamic neural networks for aircraft simulation," in Proc. 1997 IEEE Int. Conf. Systems, Man, and Cybernetics,
• Part 3 (of 5), pp. 1995–2000. [129] K.-H. Wu, C.-H. Chen, and J.-D. Lee, "Cache-genetic-based modular fuzzy neural network for robot path planning," in Proc. 1996 IEEE Int. Conf. Systems, Man and Cybernetics, Part 4 (of 4), pp. 3089–3094, 1996.
• [130] T. Ichimura, T. Takano, and E. Tazaki, "Reasoning and learning method for fuzzy rules using neural networks with adaptive structured genetic algorithm," in Proc. 1995 IEEE Int. Conf. Systems, Man and Cybernetics, Part 4 (of 5), pp. 3269-3274.
• [131] S. E. Fahlman, "Faster-learning variations on back-propagation: An empirical study," in Proc. 1988 Connectionist Models Summer School, D. S. Touretzky, G. E. Hinton, and T. J. Sejnowski, Eds. San Mateo, CA: Morgan Kaufmann, 1988, pp. 38–51.
• [132] E. M. Johansson, F. U. Dowla, and D. M. Goodman, "Backpropagation learning for multilayer feed-forward neural networks using the conjugate gradient method," Int. J. Neural Syst., vol. 2, no. 4, pp. 291-301, 1991.
• [133] H. Kitano, "Empirical studies on the speed of convergence of neural network training using genetic algorithms," in Proc. 8th Nat. Conf. AI (AAAI-90). Cambridge, MA: MIT Press, 1990, p. 789–795.
• [134] D. H. Wolpert and W. G. Macready, "No free lunch theorems for optimization," IEEE Trans. Evolutionary Computation, vol.
• 1, pp. 67–82, Apr. 1997. [135] X. Yao, "Optimization by genetic annealing," in Proc. 2nd Australian Conf. Neural Networks, Sydney, Australia, 1991, pp. 94_97
• [136] S. Omatu and S. Deris, "Stabilization of inverted pendulum by the genetic algorithm," in Proc. 1996 IEEE Conf. Emerging Technologies and Factory Automation, ETFA'96. Part 1 (of 2),

pp. 282–287. [137] S. Omatu and M. Yoshioka, "Self-tuning neuro-PID control and applications," in Proc. 1997 IEEE Int. Conf. Systems, Man, and

Cybernetics, Part 3 (of 5), pp. 1985–1989. [138] I. Erkmen and A. Ozdogan, "Short term load forecasting using genetically optimized neural network cascaded with a modified Kohonen clustering process," in Proc. 1997 IEEE Int. Symp. Intelligent Control, pp. 107-112.

• [139] J. J. Merelo, M. Patón, A. Cañas, A. Prieto, and F. Morán, "Optimization of a competitive learning neural network by genetic algorithms," in Proc. Int. Workshop Artificial Neural Networks (IWANN'93), Lecture Notes in Computer Science, vol.
• 1. Berlin, Germany: Springer-Verlag, 1993, pp. 185–192. [140] D. D. Wang and J. Xu, "Fault detection based on evolving LVQ neural networks," in Proc. 1996 IEEE Int. Conf. Systems, Man and Cybernetics, vol. 1, pp. 255-260.
• [141] S. E. Fahlman and C. Lebiere, "The cascade-correlation learning architecture," in Advances in Neural Information Processing Systems 2, D. S. Touretzky, Ed. San Mateo, CA: Morgan Kaufmann, 1990, pp. 524–532. [142] M. Frean, "The upstart algorithm: A method for constructing
• and training feedforward neural networks," Neural Computa-
• tion, vol. 2, no. 2, pp. 198–209, 1990. [143] M. C. Mozer and P. Smolensky, "Skeletonization: A technique for trimming the fat from a network via relevance assessment," Connection Sci., vol. 1, no. 1, pp. 3-26, 1989.
• [144] J. Sietsma and R. J. F. Dow, "Creating artificial neural networks that generalize," Neural Networks, vol. 4, no. 1, pp. 67-79,
• [145] Y. Hirose, K. Yamashita, and S. Hijiya, "Back-propagation algorithm which varies the number of hidden units," Neural Networks, vol. 4, no. 1, pp. 61–66, 1991.
• [146] Y. LeCun, J. S. Denker, and S. A. Solla, "Optimal brain damage," in Advances in Neural Information Processing Systems 2, D. S. Touretzky, Ed. San Mateo, CA: Morgan Kaufmann, 1990, pp. 598–605.
• [147] A. Roy, L. S. Kim, and S. Mukhopadhyay, "A polynomial time algorithm for the construction and training of a class of multilayer perceptrons," Neural Networks, vol. 6, no. 4, pp. 535-545, 1993.
• [148] J.-N. Hwang, S.-S. You, S.-R. Lay, and I.-C. Jou, "What's wrong with a cascaded correlation learning network: A projection pursuit learning perspective," Dep. Elect. Eng., Univ. Washington, Seattle, Tech. Rep. FT-10, 1993.
• [149] P. J. Angeline, G. M. Sauders, and J. B. Pollack, "An evolutionary algorithm that constructs recurrent neural networks," IEEE
• Trans. Neural Networks, vol. 5, pp. 54-65, Jan. 1994. [150] G. F. Miller, P. M. Todd, and S. U. Hegde, "Designing neural networks using genetic algorithms," in Proc. 3rd Int. Conf. Genetic Algorithms and Their Applications, J. D. Schaffer, Ed. San Mateo, CA: Morgan Kaufmann, 1989, pp. 379–384.
• [151] H. Kitano, "Designing neural networks using genetic algorithms with graph generation system," Complex Syst., vol. 4, no. 4, pp. 461-476, 1990.
• [152] S. A. Harp, T. Samad, and A. Guha, "Toward the genetic synthesis of neural networks," in Proc. 3rd Int. Conf. Genetic Algorithms and Their Applications, J. D. Schaffer, Ed. San Mateo, CA: Morgan Kaufmann, 1989, pp. 360-369.
• [153] J. D. Schaffer, R. A. Caruana, and L. J. Eshelman, "Using genetic search to exploit the emergent behavior of neural
• networks," Phys. D, vol. 42, pp. 244–248, 1990. [154] S. W. Wilson, "Perceptron redux: Emergence of structure," Phys. D, vol. 42, pp. 249–256, 1990.
• [155] N. Dodd, D. Macfarlane, and C. Marland, "Optimization of artificial neural network structure using genetic techniques implemented on multiple transputers," in Proc. Transputing'91, P. Welch, D. Stiles, T. L. Kunii, and A. Bakkers, Eds. Amsterdam, The Netherlands: IOS, 1991, pp. 687–700. [156] S. A. Harp, T. Samad, and A. Guha, "Designing application-
• specific neural networks using the genetic algorithm," in Advances in Neural Information Processing Systems 2, D. S. Touretzky, Ed. San Mateo, CA: Morgan Kaufmann, 1990, pp. 447-454.
• [157] W. B. Dress, "Darwinian optimization of synthetic neural systems," in Proc. 1st IEEE Int. Conf. Neural Networks, vol. 3, 1987, pp. 769–775.
• [158] A. Bergman and M. Kerszberg, "Breeding intelligent automata," in Proc. of the 1st IEEE Int. Conf. Neural Networks, vol. 3,

1987, pp. 63–69.

• [159] P. J. B. Hancock, "GANNET: Design of a neural net for face recognition by genetic algorithm," Center for Cognitive and Computational Neuroscience, Dep. Comput. Sci. Psychology, Stirling Univ., Stirling, U.K., Tech. Rep. CCCN-6, Aug. 1990.
• [160] C. P. Dolan and M. G. Dyer, "Toward the evolution of symbols," in Proc. 2nd Int. Conf. Genetic Algorithms and Their Applications. Hillsdale, NJ: Erlbaum, 1987, pp. 123–131.
• [161] B. Fullmer and R. Miikkulainen, "Using marker-based genetic encoding of neural networks to evolve finite-state behavior, in Toward a Practice of Autonomous Systems: Proc. 1st Europ. Conf. Artificial Life, F. J. Varela and P. Bourgine, Eds. Cambridge, MA: MIT Press, 1991, pp. 255-262.
• [162] M. Zaus and R. Megnet, "Fusion-technology and the design of evolutionary machines for neural networks," in Artificial Neural Networks: Proc. Int. Conf. Artificial Neural Networks—ICANN-91, vol. 2, T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, Eds. Amsterdam, The Netherlands: North-Holland, 1991, pp. 1165-1168.
• [163] N. Dodd, "Optimization of neural-network structure using genetic techniques," in Proc. Conf. Applications of Artificial Intelligence in Engineering VI, G. Rzevski and R. A. Adey, Eds. London, U.K.: Elsevier, 1991, pp. 939–944. [164] S. J. Marshall and R. F. Harrison, "Optimization and training of
• feedforward neural networks by genetic algorithms," in Proc. 2nd IEE Int. Conf. Artificial Neural Networks. London, U.K.:
• Inst. Elect. Eng. Press, 1991, pp. 39–43. [165] S. Oliker, M. Furst, and O. Maimon, "A distributed genetic algorithm for neural network design and training," Complex
• Syst., vol. 6, no. 5, pp. 459–477, 1992. [166] L. Marti, "Genetically generated neural networks I: Representational effects," in Proc. Int. Joint Conf. Neural Networks (IJCNN'92 Baltimore), vol. IV, pp. 537–542. [167] W. Schiffmann, M. Joost, and R. Werner, "Synthesis and per-
• formance analysis of multilayer neural network architectures, Inst. Phys., Koblenz, Univ. Koblenz, Tech. Rep. 16/1992, 1992.
• [168] H.-M. Voigt, J. Born, and I. Santibáñez-Koref, "Evolutionary structuring of artificial neural networks," Bionics and Evolution Techniques Lab., Tech. Univ. Berlin, Germany, Tech. Rep., 1993.
• [169] F. J. Marin and F. Sandoval, "Genetic synthesis of discrete-time recurrent neural network," in Proc. Int. Workshop Artificial Neural Networks (IWANN'93), Lecture Notes in Computer Science, vol. 686. Berlin, Germany: Springer-Verlag, 1993, pp. 179–184.
• [170] E. Alba, J. F. Aldana, and J. M. Troya, "Fully automatic ANN design: A genetic approach," in Proc. Int. Workshop Artificial Neural Networks (IWANN'93), Lecture Notes in Computer Science, vol. 686. Berlin, Germany: Springer-Verlag, 1993, pp. 399-404.
• [171] D. White and P. Ligomenides, "GANNet: A genetic algorithm for optimizing topology and weights in neural network design," in Proc. Int. Workshop Artificial Neural Networks (IWANN'93), Lecture Notes in Computer Science, vol. 686. Berlin, Germany: Springer-Verlag, 1993, pp. 322–327.
• [172] H. Andersen, "A constructive algorithm for a multilayer perceptron based on co-operative population concepts in genetic algorithms," Master's thesis, Dep. Elect. Comput. Eng., Univ. Queensland, Brisbane, Australia, Sept. 1993. [173] D. H. Gariglio and A. J. Helget, "Identification and control of a
• simulated distillation plant using connectionist and evolutionary techniques," Simulation, vol. 63, no. 6, pp. 393-404, 1994.
• [174] L. A. Belfore, II, and A.-R. A. Arkadan, "Modeling faulted switched reluctance motors using evolutionary neural networks," IEEE Trans. Ind. Electron., vol. 44, pp. 226-233, Feb. 1997.
• [175] A. Dobnikar, "Evolutionary design of application-specific neural networks: A genetic approach," Neural Network World, vol. 5, no. 1, pp. 41–50, 1995.
• [176] Y. Sato and T. Furuya, "Coevolution in recurrent neural networks using genetic algorithms," Syst. Comput. Japan, vol. 27, no. 5, pp. 64-73, 1996.
• [177] F. Mondada and D. Floreano, "Evolution of neural control structures: Some experiments on mobile robots," Robot. Autonomous

• Syst., vol. 16, nos. 2–4, pp. 183–195, 1995. [178] H. Ishigami, T. Fukuda, and F. Arai, "Structure optimization of fuzzy neural network by genetic algorithm," Fuzzy Sets Syst., vol. 71, no. 3, pp. 257–264, 1995.

• [179] J. Fang and Y. Xi, "Neural network design based on evolutionary programming," Artificial Intell. Eng., vol. 11, no. 2, pp. 155–161, 1997.

• [180] C. Nikolopoulos and P. Fellrath, "Hybrid expert system for investment advising," Expert Syst., vol. 11, no. 4, pp. 245–248, 1994
• [181] R. E. Smith and I. H. B. Cribbs, "Combined biological paradigms: A neural, genetics-based autonomous systems strategy," Robot. Autonomous Syst., vol. 22, no. 1, pp. 65–74, 1997.
• [182] V. Maniezzo, "Genetic evolution of the topology and weight distribution of neural networks," IEEE Trans. Neural Networks, vol. 5, pp. 39–53, Jan. 1994.
• [183] J. Sklansky and M. Vriesenga, "Genetic selection and neural modeling of piecewise linear classifiers," Int. J. Pattern Recognition Artificial Intell., vol. 10, no. 5, pp. 587–612, 1996.
• [184] X. Yao and Y. Shi, "A preliminary study on designing artificial neural networks using co-evolution," in Proc. IEEE Singapore Int. Conf. Intelligent Control and Instrumentation, Singapore, June 1995, pp. 149–154.
  [185] X. Yao and Y. Liu, "EPNet for chaotic time-series prediction,"
• [185] X. Yao and Y. Liu, "EPNet for chaotic time-series prediction," in Select. Papers 1st Asia-Pacific Conf. Simulated Evolution and Learning (SEAL'96), vol. 1285 of Lecture Notes in Artificial Intelligence, X. Yao, J.-H. Kim, and T. Furuhashi, Eds. Berlin, Germany: Springer-Verlag, 1997, pp. 146–156.
• [186] Y. Liu and X. Yao, "A population-based learning algorithm which learns both architectures and weights of neural networks," Chinese J. Advanced Software Res., vol. 3, no. 1, pp. 54–65, 1996.
• [187] X. Yao and Y. Liu, "Toward designing artificial neural networks by evolution," Appl. Math. Computation, vol. 91, no. 1, pp. 83–90, 1998.
• [188] _____, "Evolutionary artificial neural networks that learn and generalize well," in Proc. 1996 IEEE Int. Conf. Neural Networks, Washington, DC, June 3–6, 1996, pp. 159–164.
• works, Washington, DC, June 3–6, 1996, pp. 159–164.

[189] _____, "Evolving artificial neural networks for medical applications," in Proc. 1995 Australia-Korea Joint Workshop Evolutionary Computation, KAIST, Taejon, Korea, Sept. 1995, pp. 1–16
- [190] X. Yao, "The importance of maintaining behavioral link between parents and offspring," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation (ICEC'97), Indianapolis, IN, Apr. 1997, pp. 629–633.
- [191] Y. Liu and X. Yao, "Evolutionary design of artificial neural networks with different nodes," in Proc. 1996 IEEE Int. Conf. Evolutionary Computation (ICEC'96), Nagoya, Japan, pp. 670–675.
- [192] X. Yao and Y. Liu, "Ensemble structure of evolutionary artificial neural networks," in Proc. 1996 IEEE Int. Conf. Evolutionary Computation (ICEC'96), Nagoya, Japan, pp. 659–664.
- [193] _____, "Making use of population information in evolutionary artificial neural networks," IEEE Trans. Syst., Man, Cyber. B, vol. 28, pp. 417–425, Mar. 1998.
- vol. 28, pp. 417–425, Mar. 1998.
[194] _____, "A new evolutionary system for evolving artificial neural networks," IEEE Trans. Neural Networks, vol. 8, pp. 694–713, May 1997.
- [195] _____, "Evolving artificial neural networks through evolutionary programming," in Evolutionary Programming V: Proc. 5th Annu. Conf. Evolutionary Programming, L. J. Fogel, P. J. Angeline, and T. Bäck, Eds. Cambridge, MA: MIT Press, 1996, pp. 257–266.
- [196] J. R. McDonnell and D. E. Waagen, "Evolving cascade-correlation networks for time-series forecasting," Int. J. Artificial Intell. Tools, vol. 3, no. 3, pp. 327–338, 1995.
- Artificial Intell. Tools, vol. 3, no. 3, pp. 327–338, 1995.
[197] J. R. McDonnell and D. Waagen, "Evolving recurrent perceptrons for time-series modeling," IEEE Trans. Neural Networks, vol. 5, pp. 24–38, Jan. 1994.
- [198] J. C. F. Pujol and R. Poli, "Evolving the topology and the weights of neural networks using a dual representation," Appl. Intell., vol. 8, no. 1, pp. 73–84, 1998.
- Intell., vol. 8, no. 1, pp. 73–84, 1998.
[199] N. Richards, D. E. Moriarty, and R. Miikkulainen, "Evolving neural networks to play Go," Appl. Intell., vol. 8, no. 1, pp. 85–96, 1998.
- [200] D. Moriarty and R. Miikkulainen, "Discovering complex othello strategies through evolutionary neural networks," Connection Sci., vol. 7, nos. 3/4, pp. 195–210, 1995.
- [201] R. Smalz and M. Conrad, "Combining evolution with credit apportionment: A new learning algorithm for neural nets,"

• Neural Networks, vol. 7, no. 2, pp. 341-351, 1994.
• [202] B. Kothari, B. Paya, and I. Esat, "Machinery fault diagnostics using direct encoding graph syntax for optimizing artificial neural network structure," in Proc. 1996 3rd Biennial Joint Conf. Engineering Systems Design and Analysis, ESDA, Part 7 (of 9). New York: ASME, 1996, pp. 205–210.
• [203] C. R. Chow and C. H. Chu, "Configuration of multilayered feedforward networks by an evolutionary process," in Proc. 37th Midwest Symp. Circuits and Systems, Part 1 (of 2), 1994, pp. 531–534
• [204] S. Dreiseitl and W. Jacak, "Genetic algorithm based neural networks for dynamical system modeling," in Proc. 1995 IEEE Int. Conf. Evolutionary Computation, Part 2 (of 2), pp. 602–607.
• [205] E. Vonk, L. C. Jain, and R. Johnson, "Using genetic algorithms with grammar encoding to generate neural networks," in Proc. 1995 IEEE Int. Conf. Neural Networks, Part 4 (of 6), pp. 1928–1931.
• [206] S.-B. Cho and K. Shimohara, "Modular neural networks evolved by genetic programming," in Proc. 1996 IEEE Int. Conf. Evolutionary Computation, ICEC'96, pp. 681–684.
• [207] D. H. F. Yip, E. L. Hines, and W. W. H. Yu, "Application of artificial neural networks in sales forecasting," in Proc. 1997 IEEE Int. Conf. Neural Networks, Part 4 (of 4), pp. 2121–2124.
• [208] C. A. Perez and C. A. Holzmann, "Improvements on hand-written digit recognition by genetic selection of neural network topology and by augmented training," in Proc. 1997 IEEE Int. Conf. Systems, Man, and Cybernetics, Part 2 (of 5), pp. 1487–1491.
• [209] K. Shirakawa and N. Okubo, "Genetic determination of large-signal HEMT model," in Proc. 1997 27th Europ. Microwave Conf. Part J. (of 2). Turnbridge Wells, U.K., pp. 432–436.
• Conf, Part 1 (of 2), Turnbridge Wells, U.K., pp. 432–436.

[210] N. Snoad and T. Bossomaier, "MONSTER—The ghost in the connection machine: Modularity of neural systems in theoretical evolutionary research," in Proc. 1995 ACM/IEEE Supercomputing Conf. Los Alamitos, CA: IEEE Computer Soc., 1995, pp. 578–601.
- [211] T. Ragg and S. Gutjahr, "Automatic determination of optimal network topologies based on information theory and evolution," in Proc. 1997 23rd EUROMICRO Conf.. Los Alamitos, CA: IEEE Computer Soc., 1997, pp. 549–555.
- [212] S. D. Likothanassis, E. Georgopoulos, and D. Fotakis, "Optimizing the structure of neural networks using evolution techniques," in Proc. 5th Int. Conf. Application of High-Performance Computers in Engineering. Ashurst, U.K.: Computational Mechanics, 1997, pp. 157–168.
- [213] D. Patel, "Using genetic algorithms to construct a network for financial prediction," in Proc. SPIE: Applications of Artificial Neural Networks in Image Processing, Bellingham, WA, 1996, pp. 204–213.
[214] D. E. Moriarty and R. Miikkulainen, "Improving game-tree
- [214] D. E. Moriarty and R. Miikkulainen, "Improving game-tree search with evolutionary neural networks," in Proc. 1st IEEE Conf. Evolutionary Computation. Part 1 (of 2), 1994, pp. 496–501.
- [215] S. G. Romaniuk, "Applying crossover operators to automatic neural network construction," in Proc. 1st IEEE Conf. Evolutionary Computation, Part 2 (of 2), 1994, pp. 750–752.
- tionary Computation. Part 2 (of 2), 1994, pp. 750–752.

[216] _____, "Toward minimal network architectures with evolutionary growth networks," in Proc. 1994 IEEE Int. Conf. Neural Networks, Part 3 (of 7), pp. 1710–1712.
- Networks, Part 3 (of 7), pp. 1710–1712.

[217] C.-H. Lee and J. H. Kim, "Evolutionary ordered neural network with a linked-list encoding scheme," in Proc. 1996 IEEE Int. Conf. Evolutionary Computation, ICEC'96, pp. 665–669.
- [218] A. I. Esparcia-Alcazar and K. C. Sharman, "Genetic programming techniques that evolve recurrent neural network architectures for signal processing," in Proc. 1996 IEEE Workshop Neural Networks for Signal Processing, pp. 139–148.
- shop Neural Networks for Signal Processing, pp. 139–148.

[219] Z. Q. Bo, H. Y. Li, R. K. Aggarwal, A. T. Johns, and P. J. Moore, "Non-communication protection of transmission line based on genetic evolved neural network," in Proc. 1997 6th Int. Conf. Developments in Power System Protection, Stevenage, U.K. Inst. Elect. Eng. Conf. Pub. 434, 1997, pp. 291–294.
- U.K., Inst. Elect. Eng. Conf. Pub. 434, 1997, pp. 291–294.

[220] Z. Q. Bo, H. Y. Li, R. K. Aggarwal, and A. T. Johns,
"Current transients based faulted phase selection technique using a genetic algorithm evolved neural network," in Proc. 1997 32nd Universities Power Engineering Conf., UPEC'97,
Part 2 (of 2). Iraklio, Greece: Technological Educational Inst.,
1997, pp. 959–962.
- [221] Y. H. Song, A. T. Johns, Q. Y. Xuan, and J. Y. Liu, "Genetic

• algorithm based neural networks applied to fault classification for EHV transmission lines with a UPFC," in Proc. 1997 6th Int. Conf. Developments in Power System Protection, Stevenage, U.K., Inst. Elect. Eng. Conf. Pub. 434, 1997, pp. 278-281.
• [222] Q. Zhao, "EditEr: A combination of IEA and CEA," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation, ICEC'97, pp. 641–645.
• [223] M. Sarkar and B. Yegnanarayana, "Feedforward neural networks configuration using evolutionary programming," in Proc. 1997 IEEE Int. Conf. Neural Networks, Part 1 (of 4), pp. 438–443.
• [224] S. B. Cho, "Combining modular neural networks developed
• by evolutionary algorithm," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation, ICEC'97, pp. 647–650.

[225] M. W. Hwang, J. Y. Choi, and J. Park, "Evolutionary projection neural networks," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation, ICEC'97, pp. 667-671.
- [226] M. Bichsel and P. Seitz, "Minimum class entropy: A maximum information approach to layered networks," Neural Networks,
- vol. 2, no. 2, pp. 133–141, 1989. [227] D. B. Fogel, "An information criterion for optimal neural network selection," IEEE Trans. Neural Networks, vol. 2, pp. 490-497, Sept. 1991.
- [228] J. Utans and J. Moody, "Selecting neural network architectures via the prediction risk: Application to corporate bond rating prediction," in Proc. 1st Int. Conf. AI Applications on Wall Street. Los Alamitos, CA: IEEE Computer Soc., 1991, pp. 35-41
- [229] W. M. Spears and V. Anand, "A study of crossover operators in genetic programming," in Proc. 6th Int. Symp. Methodologies for Intelligent Systems (ISMIS'91), Z. W. Ras and M. Zemankova, Eds. Berlin, Germany: Springer-Verlag, 1991, pp. 409-418
- [230] E. Mjolsness, D. H. Sharp, and B. K. Alpert, "Scaling, machine learning, and genetic neural nets," Advances in Applied Math., vol. 10, pp. 137-163, 1989.
- [231] J. W. L. Merrill and R. F. Port, "Fractally configured neural networks," Neural Networks, vol. 4, no. 1, pp. 53–60, 1991. [232] F. Gruau, "Genetic synthesis of boolean neural networks with
- a cell rewriting developmental process," in Proc. Int. Workshop Combinations of Genetic Algorithms and Neural Networks (COGANN-92), D. Whitley and J. D. Schaffer, Eds. Los Alamitos, CA: IEEE Computer Soc., 1992, pp. 55–74. [233] A. A. Siddiqi and S. M. Lucas, "A comparison of matrix
- rewriting versus direct encoding for evolving neural networks," in Proc. 1998 IEEE Int. Conf. Evolutionary Computation, pp. 392_397
- [234] S. S. Wilson, "Teaching network connectivity using simulated annealing on a massively parallel processor," Proc. IEEE, vol. 79, pp. 559–566, Apr. 1991.
- [235] H. H. Szu and R. L. Hartley, "Nonconvex optimization by fast simulated annealing," Proc. IEEE, vol. 75, pp. 1538–1540, Nov.
- [236] H. C. Andersen and A. C. Tsoi, "A constructive algorithm for the training of a multilayer perceptron based on the genetic
- algorithm," Complex Syst., vol. 7, no. 4, pp. 249–268, 1993. [237] R. E. Smith and H. B. Cribbs III, "Is a learning classifier system a type of neural network," Evolutionary Computation, vol. 2,
- no. 1, pp. 19–36, Spring 1994. [238] G. Mani, "Learning by gradient descent in function space," in Proc. IEEE Int. Conf. System, Man, and Cybernetics, Los
- Angeles, CA, 1990, pp. 242–247. [239] D. R. Lovell and A. C. Tsoi, The Performance of the Neocogni tron with Various S-Cell and C-Cell Transfer Functions, Intell. Machines Lab., Dep. Elect. Eng., Univ. Queensland, Tech. Rep., Apr. 1992.
- [240] B. DasGupta and G. Schnitger, "Efficient approximation with neural networks: A comparison of gate functions," Dep. Comput. Sci., Pennsylvania State Univ., University Park, Tech. Rep., 1992
- [241] D. G. Stork, S. Walker, M. Burns, and B. Jackson, "Preadaptation in neural circuits," in Proc. Int. Joint Conf. Neural Networks, vol. I, Washington, DC, 1990, pp. 202-205.
- [242] A. V. Sebald and K. Chellapilla, "On making problems evolutionarily friendly, part I: Evolving the most convenient representations," in Evolutionary Programming VII: Proc. 7th Annu. Conf. Evolutionary Programming, vol. 1447 of Lecture Notes in Computer Science, V. W. Porto, N. Saravanan, D. Waagen, and

• A. E. Eiben, Eds. Berlin, Germany: Springer-Verlag, 1998,
• pp. 271–280. [243] D. B. Fogel, "Phenotypes, genotypes, and operators in evolutionary computation," in Proc. 1995 IEEE Int. Conf. Evolutionary Computation (ICEC'95), Perf., Australia, pp. 193–198.
• [244] D. E. Rumelhart and J. L. McClelland, Eds., Parallel Distributed Processing: Explorations in the Microstructures of Cognition. Cambridge, MA: MIT Press, 1986.
• [245] S. Jockusch and H. Ritter, "Self-organizing maps: Local competition and evolutionary optimization," Neural Networks, vol. 7, no. 8, pp. 1229–1239, 1994.
• [246] Q. Zhao and T. Higuchi, "Evolutionary learning of nearest-neighbor MLP," IEEE Trans. Neural Networks, vol. 7, pp. 762-767, May 1996.
• [247] Q. Zhao, "Stable on-line evolutionary learning of NN-MLP," IEEE Trans. Neural Networks, vol. 8, pp. 1371–1378, Nov.
• [248] Q. Zhao and T. Higuchi, "Efficient learning of NN-MLP based on individual evolutionary algorithm," Neurocomput., vol. 13, nos. 2-4, pp. 201-215, 1996.
• [249] B. A. Whitehead and T. D. Choate, "Cooperative-competitive genetic evolution of radial basis function centers with widths for time series prediction," IEEE Trans. Neural Networks, vol. 7, pp. 869–880, July 1996. [250] B. A. Whitehead, "Genetic evolution of radial basis function
• coverage using orthogonal niches," IEEE Trans. Neural Networks, vol. 7, pp. 1525-1528, Nov. 1996.
• [251] S. A. Billings and G. L. Zheng, "Radial basis function network configuration using genetic algorithms," Neural Networks, vol. 8, no. 6, pp. 877-890, 1995.
• [252] B. A. Whitehead and T. D. Choate, "Evolving space-filling curves to distribute radial basis functions over an input space,
• IEEE Trans. Neural Networks, vol. 5, pp. 15–23, Jan. 1994. [253] E. P. Maillard and D. Gueriot, "RBF neural network, basis functions and genetic algorithms," in Proc. 1997 IEEE Int. Conf. Neural Networks. Part 4 (of 4), pp. 2187-2190.
• [254] Y. Liu and X. Yao, "A population-based learning algorithm which learns both architectures and weights of neural networks," in Proc. ICYCS'95 Workshop Soft Computing, Beijing,
• China, 1995, pp. 29–38. [255] A. Artola, S. Broecher, and W. Singer, "Different voltagedependent thresholds for inducing long-term depression and long-term potentiation in slices of rat visual cortex," Nature, vol. 347, no. 6288, pp. 69-72, Sept. 1990.
• [256] P. J. B. Hancock, L. S. Smith, and W. A. Phillips, "A biologically supported error-correcting learning rule," in Proc. Int. Conf. Artificial Neural Networks—ICANN-91, vol. 1, T. Kohonen, K. Mäkisara, O. Simula, and J. Kangas, Eds. Amsterdam, The Netherlands: North-Holland, 1991, pp. 531-536.
• [257] J. M. Smith, "When learning guides evolution," Nature, vol. 329, no. 6142, pp. 761–762, Oct. 1987.
• [258] G. E. Hinton and S. J. Nowlan, "How learning can guide evolution," Complex Syst., vol. 1, no. 3, pp. 495–502, 1987.
• [259] R. K. Belew, "Evolution, learning and culture: Computational metaphors for adaptive algorithms," Comput. Sci. Eng. Dep. (C-014), Univ. of California, San Diego, Tech. Rep. #CS89-156, Sept. 1989.
• [260] S. Nolfi, J. L. Elman, and D. Parisi, "Learning and evolution in neural networks," Center Res. Language, Univ. California, San
• Diego, July Tech. Rep. CRT-9019, 1990. [261] H. Mühlenbein and J. Kindermann, "The dynamics of evolution and learning—Toward genetic neural networks," in Connectionism in Perspective, R. Pfeifer et al., Eds. Amsterdam, The Netherlands: Elsevier, pp. 173-198, 1989.
• [262] H. Mühlenbein, "Adaptation in open systems: Learning and evolution," in Workshop Konnektionismus, J. Kindermann and C. Lischka, Eds. Germany: GMD, 1988, pp. 122-130.
• [263] J. Paredis, "The evolution of behavior: Some experiments," in Proc. 1st Int. Conf. Simulation of Adaptive Behavior: From Animals to Animats, J. Meyer and S. W. Wilson, Eds. Cambridge,
• MA: MIT Press, 1991. [264] D. J. Chalmers, "The evolution of learning: An experiment in genetic connectionism," in Proc. 1990 Connectionist Models Summer School, D. S. Touretzky, J. L. Elman, and G. E. Hinton, Eds. San Mateo, CA: Morgan Kaufmann, 1990, pp. 81–90. [265] Y. Bengio and S. Bengio, "Learning a synaptic learning

• rule," Dép. Informatique et de Recherche Opérationelle, Univ. Montréal, Canada, Tech. Rep. 751, Nov. 1990.

• [266] S. Bengio, Y. Bengio, J. Cloutier, and J. Gecsei, "On the optimization of a synaptic learning rule," in Preprints Conf. Optimality in Artificial and Biological Neural Networks, Univ. of Texas, Dallas, Feb. 6-8, 1992

• [267] J. F. Fontanari and R. Meir, "Evolving a learning algorithm for the binary perceptron," Network, vol. 2, no. 4, pp. 353–359, Nov. 1991
• [268] D. H. Ackley and M. S. Littman, "Interactions between learning and evolution," in Artificial Life II, SFI Studies in the Sciences of Complexity, Vol. X, C. G. Langton, C. Taylor, J. D. Farmer, and S. Rasmussen, Eds. Reading, MA: Addison-Wesley, 1991, pp. 487 - 509.
• [269] J. Baxter, "The evolution of learning algorithms for artificial neural networks," in Complex Systems, D. Green and T. Bossomaier, Eds. Amsterdam, The Netherlands: IOS, pp. 313-326, 1992.
• [270] D. Crosher, "The artificial evolution of a generalized class of adaptive processes," in Preprints AI'93 Workshop Evolutionary
• Computation, Nov. 1993, pp. 18–36. [271] P. Turney, D. Whitley, and R. Anderson, Eds., Evolutionary Computation (Special Issue on the Baldwin Effect), vol. 4, no.
• 3, pp. 213–329, 1996. [272] H. B. Kim, S. H. Jung, T. G. Kim, and K. H. Park, "Fast learning method for back-propagation neural network by evolutionary adaptation of learning rates," Neurocomput., vol. 11, no. 1, pp. 101–106, 1996.
• [273] R. A. Jacobs, "Increased rates of convergence through learning rate adaptation," Neural Networks, vol. 1, no. 3, pp. 295-307,
• [274] B. Widrow and M. E. Hoff, "Adaptive switching circuits," in 1960 IRE WESTCON Convention Rec., pp. 96–104, 1960.
• [275] D. Parasi, F. Cecconi, and S. Nolfi, "Econets: Neural networks that learn in an environment," Network, vol. 1, no. 2, pp. 149-168, Apr. 1990.
• [276] M. N. Narayanan and S. B. Lucas, "A genetic algorithm to improve a neural network to predict a patient's response to Warfarin," Methods Inform. Med., vol. 32, pp. 55-58, 1993.
• [277] Z. Guo and R. E. Uhrig, "Using genetic algorithms to select inputs for neural networks," in Proc. Int. Workshop Combinations of Genetic Algorithms and Neural Networks (COGANN-92), D. Whitley and J. D. Schaffer, Eds. Los Alamitos, CA: IEEE Computer Soc., 1992, pp. 223-234.
• [278] F. Z. Brill, D. E. Brown, and W. N. Martin, "Fast genetic selection of features for neural network classifiers," IEEE Trans.
• Neural Networks, vol. 3, pp. 324–328, Mar. 1992.
  [279] L. S. Hsu and Z. B. Wu, "Input pattern encoding through generalized adaptive search," in Proc. Int. Workshop Combinations of Genetic Algorithms and Neural Networks (COGANN-92), D. Whitley and J. D. Schaffer, Eds. Los Alamitos, CA: IEEE
• Computer Soc., 1992, pp. 235–247. [280] E. J. Chang and R. P. Lippmann, "Using genetic algorithms to improve pattern classification performance," in Advances in Neural Information Processing Systems (3), R. P. Lippmann, J. E. Moody, and D. S. Touretzky, Eds. San Mateo, CA: Morgan Kaufmann, 1991, pp. 797-803.
• [281] J. Hornyak and L. Monostori, "Feature extraction technique for ANN-based financial forecasting," Neural Network World, vol. 7, nos. 4–5, pp. 543–552, 1997.
• [282] S. M. Yamany, K. J. Khiani, and A. A. Farag, "Applications of neural networks and genetic algorithms in the classification of enothelial cells," Pattern Recognition Lett., vol. 18, nos. 11-13, pp. 1205-1210, 1997.
• [283] B. Back, T. Laitinen, and K. Sere, "Neural networks and genetic algorithms for bankruptcy predictions," Expert Syst. Applicat.: Int. J., vol. 11, no. 4, pp. 407-413, 1996.
• [284] F. Dellaert and J. Vandewalle, "Automatic design of cellular neural networks by means of genetic algorithms: Finding a feature detector," in Proc. IEEE Int. Workshop Cellular Neural
• Networks and Their Applications, 1994, pp. 189–194. [285] P. R. Weller, R. Summers, and A. C. Thompson, "Using a genetic algorithm to evolve an optimum input set for a predictive neural network," in Proc. 1st IEE/IEEE Int. Conf. Genetic Algorithms in Engineering Systems: Innovations and Applications (GALESIA'95), Stevenage, U.K., Inst. Elect. Eng.

• Conf. Pub. 414, 1995, pp. 256–258. [286] M. A. Kupinski and M. L. Maryellen, "Feature selection and classifiers for the computerized detection of mass lesions in digital mammography," in Proc. 1997 IEEE Int. Conf. Neural

• Networks. Part 4 (of 4), pp. 2460–2463.

• [287] A. D. Brown and H. C. Card, "Evolutionary artificial neural networks," in Proc. 1997 Canadian Conf. Electrical and Computer Engineering, CCECE'97. Part 1 (of 2), pp. 313–317.
• [288] B.-T. Zhang and G. Veenker, "Neural networks that teach themselves through genetic discovery of novel examples," in Proc. 1991 IEEE Int. Joint Conf. Neural Networks (IJCNN'91
• Singapore), vol. 1, pp. 690–695. [289] S. Cho and K. Cha, "Evolution of neural network training set through addition of virtual samples," in Proc. 1996 IEEE Int. Conf. Evolutionary Computation, ICEC'96, pp. 685-688.
• [290] Z. Michalewicz, C. Z. Janikow, and J. B. Krawczyk, "A modified genetic algorithm for optimal control problems," Comput. Math. Applicat., vol. 23, no. 12, pp. 83-94, 1992.
• [291] D. B. Fogel, "Applying evolutionary programming to selected control problems," Comput. Math. Applicat., vol. 27, no. 11, pp. 89–104, 1994. [292] J. Bobbin and X. Yao, "Solving optimal control problems with a
• cost on changing control by evolutionary algorithms," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation (ICEC'97), Indianapolis, IN, pp. 331-336.
• [293] T. Morimoto, J. de Baerdemaeker, and Y. Hashimoto, "Intelligent approach for optimal control of fruit-storage process using neural networks and genetic algorithms," Comput. Electron.
• Agriculture, vol. 18, nos. 2–3, pp. 205–224, 1997. [294] T. Morimoto, J. Suzuki, and Y. Hashimoto, "Optimization of a fuzzy controller for fruit storage using neural networks and genetic algorithms," Eng. Applicat. Artificial Intell., vol. 10, no. 5, pp. 453–461, 1997.
• [295] N. Noguchi and H. Terao, "Path planning of an agricultural mobile robot by neural network and genetic algorithm," Comput.
• Electron. Agriculture, vol. 18, nos. 2–3, pp. 187–204, 1997. [296] L.-D. Chou and J.-L. C. Wu, "Bandwidth allocation of virtual paths using neural-network-based genetic algorithms," Proc. Inst. Elect. Eng. Commun., vol. 145, no. 1, pp. 33-39, 1998.
• _, "Parameter adjustment using neural-network-based genetic algorithms for guaranteed QOS in atm networks," IEICE Trans. Commun., vol. E78-B, no. 4, pp. 572–579, 1995. [298] D. H. Wolpert, "A mathematical theory of generalization,"
• Complex Syst., vol. 4, no. 2, pp. 151-249, 1990.
• [299] J. Rissanen, "Modeling by shortest data description," Automatica, vol. 14, no. 5, pp. 465–471, Sept. 1978.
• [300] H. Akaike, "A new look at the statistical model identification," IEEE Trans. Automat. Contr., vol. AC-19, pp. 716-723, Dec. 1974.
• [301] C. S. Wallace and J. D. Patrick, "Coding decision trees," Dep. Comput. Sci., Monash University, Clayton, Victoria, Australia, Tech. Rep. 91/153, Aug. 1991.
• [302] X. Yao, Y. Liu, and P. Darwen, "How to make best use of evolutionary learning," in Complex Systems: From Local Interactions to Global Phenomena, R. Stocker, H. Jelinek, and B. Durnota, Eds. Amsterdam, The Netherlands: IOS, 1996,
• pp. 229–242. [303] P. G. Harrald and M. Kamstra, "Evolving artificial neural networks to combine financial forecasts," IEEE Trans. Evolu-
• tionary Computation, vol. 1, pp. 40–51, Apr. 1997. [304] Y. Liu and X. Yao, "Toward designing neural network ensembles by evolution," in Parallel Problem Solving from Nature (PPSN) V, vol. 1498 of Lecture Notes in Computer Science, A. E. Eiben, T. Bäck, M. Schoenauer, and H.-P. Schwefel, Eds. Berlin, Germany: Springer-Verlag, 1998, pp. 623-632.
• [305] S. Wesolkowski and K. Hassanein, "Comparative study of combination schemes for an ensemble of digit recognition neural networks," in Proc. 1997 IEEE Int. Conf. Systems, Man,
• and Cybernetics. Part 4 (of 5), pp. 3534–3539, 1997. [306] R. A. Zitar and M. H. Hassoun, "Neurocontrollers trained with rules extracted by a genetic assisted reinforcement learning system," IEEE Trans. Neural Networks, vol. 6, pp. 859–878, July 1995.
• [307] A. Imada and K. Araki, "Application of an evolution strategy to the Hopfield model of associative memory," in Proc. 1997 IEEE Int. Conf. Evolutionary Computation, ICEC'97, pp. 679–683. [308] P. P. C. Yip and Y.-H. Pao, "Combinatorial optimization with
• use of guided evolutionary simulated annealing," IEEE Trans.
• Neural Networks, vol. 6, no. 2, pp. 290–295, 1995. [309] D. W. Coit and A. E. Smith, "Solving the redundancy allocation problem using a combined neural network/genetic algorithm approach," Comput. Oper. Res., vol. 23, no. 6, pp. 515-526,

1996

[310] M. Kishimoto, K. Sakasai, K. Ara, T. Fujita, and Y. Suzuki, "Reconstruction of plasma current profile of tokamaks using combinatorial optimization techniques," IEEE Trans. Plasma Sci., vol. 24, pp. 528–538, Apr. 1996. [311] L. L. Rogers, F. U. Dowla, and V. M. Johnson, "Optical field-

scale groundwater remediation using neural networks and the genetic algorithms," Environmental Sci. Technol., vol. 29, no.

5, pp. 1145–1156, 1995. [312] J. S. Huang and H.-C. Liu, "Object recognition using genetic algorithms with a Hopfield's neural model," Expert Syst. Applicat., vol. 13, no. 3, pp. 191–199, 1997.
[313] J.-V. Potvin, D. Dube, and C. Robillard, "Hybrid approach to

vehicle routing using neural networks and genetic algorithms,"

• Appl. Intell., vol. 6, no. 3, pp. 241–252, 1996.
  [314] C. H. Dagli and P. Poshyanonda, "New approaches to nesting rectangular patterns," J. Intell. Manufact., vol. 8, no. 3, pp. 177-190, 1997.
• [315] H. C. Lee and C. H. Dagli, "Parallel genetic-neuro scheduler for job-shop scheduling problems," Int. J. Production Econ., vol. 51, nos. 1–2, pp. 115–122, 1997. [316] S. Sette, L. Boullart, and P. Kiekens, "Optimizing the
• fiber-to-yarn production process with a combined neural network/genetic algorithm approach," Textile Res. J., vol. 67, no. 2, pp. 84-92, 1997.
• [317] S.-S. Han and G. S. May, "Using neural network process models to perform PECVD silicon dioxide recipe synthesis via genetic algorithms," IEEE Trans. Semiconduct. Manufact., vol. 10, pp. 279–287, May 1997.
• [318] N. Funabiki, J. Kitamichi, and S. Nishikawa, "Evolutionary neural network algorithm for max cut problems," in Proc. 1997 IEEE Int. Conf. Neural Networks, Part 2 (of 4), pp. 1260-1265.

[319] G. Weiss, "Combining neural and evolutionary learning: Aspects and approaches," Institut für Informatik, Technische Univ. München, Germany, Tech. Rep. FKI-132-90, May 1990.

Xin Yao (Senior Member, IEEE) received the B.Sc. degree from the University of Science and Technology of China (USTC), Hefei, Anhui, China, in 1982, the M.Sc. degree from the North China Institute of Computing Technologies (NCI), Beijing, in 1985, and the Ph.D. degree from USTC in 1990.

He is a Professor of Computer Science at the School of Computer Science, University of Birmingham, U.K. He was an Associate Professor in the School of Computer Science, Uni-

versity College, the University of New South Wales, Australian Defence Force Academy (ADFA), Canberra, before joining the University of Birmingham. He held postdoctoral fellowships in the Australian National University (ANU) and the Commonwealth Scientific and Industrial Research Organization (CSIRO) in 1990-1992.

Dr. Yao was the Program Committee Cochair of CEC'99, ICCIMA'99, IEEE ICEC'98, SEAL'98, IEEE ICEC'97, and SEAL'96. He is an Associate Editor of IEEE Transactions on Evolutionary Computation and Knowledge and Information Systems: An International Journal, He is a member of the editorial board of the Journal of Cognitive Systems Research, a member of the IEEE NNC Technical Committee on Evolutionary Computation, and the Second Vice-President of the Evolutionary Programming Society.