title: Evolution Strategies at Scale: LLM Fine-Tuning Beyond Reinforcement Learning
url: http://arxiv.org/abs/2509.24372v1
EVOLUTION STRATEGIES AT SCALE: LLM FINE-TUNING BEYOND REINFORCEMENT LEARNING
Xin Qiu ∗ † Cognizant AI Lab Yulu Gan ∗ ‡ MIT Conor F. Hayes ∗ Cognizant AI Lab Qiyao Liang ‡ MIT
Elliot Meyerson Cognizant AI Lab Babak Hodjat Cognizant AI Lab Risto Miikkulainen Cognizant AI Lab, UT Austin
ABSTRACT
Fine-tuning pre-trained large language models (LLMs) for down-stream tasks is a critical step in the AI deployment pipeline. Reinforcement learning (RL) is arguably the most prominent fine-tuning method, contributing to the birth of many state-of-the-art LLMs. In contrast, evolution strategies (ES), which once showed comparable performance to RL on models with a few million parameters, was neglected due to the pessimistic perception of its scalability to larger models. In this work, we report the first successful attempt to scale up ES for fine-tuning the full parameters of LLMs, showing the surprising fact that ES can search efficiently over billions of parameters and outperform existing RL fine-tuning methods in multiple respects, including sample efficiency, tolerance to long-horizon rewards, robustness to different base LLMs, less tendency to reward hacking, and more stable performance across runs. It therefore serves as a basis to unlock a new direction in LLM fine-tuning beyond what current RL techniques provide. The source codes are provided at: https://github.com/VsonicV/es-fine-tuning-paper.
1 INTRODUCTION
The rapid development of more capable large language models (LLMs; Touvron et al., 2023; Achiam et al., 2024; AI@Meta, 2024; Jiang et al., 2024; Liu et al., 2024; Anthropic, 2025; Google, 2025) has made many scientific and engineering domains amenable to AI-based automation (Singhal et al., 2023; Wu et al., 2023; Roziere et al., 2024; Romera-Paredes et al., 2024). As a result, fine-tuning the ` pre-trained models to accommodate specific tasks and to improve alignment with user preferences has become an important part of the LLM deployment pipeline (Ouyang et al., 2022; Rafailov et al., 2023; Latif & Zhai, 2024; Guo et al., 2025a). Reinforcement learning (RL) is currently the predominant choice for such fine-tuning (Ouyang et al., 2022; Bai et al., 2022; Shao et al., 2024; Guo et al., 2025a;b; Srivastava & Aggarwal, 2025). Several challenges have emerged: First, RL methods incur low sample efficiency (Vemula et al., 2019) and high variance of the gradient estimator (Salimans et al., 2017; Sutton & Barto, 2018) when handling long-horizon rewards, which is a common case for LLM fine-tuning with outcome-only rewards. Proper credit assignment at token level for RL fine-tuning methods is difficult (Zhang et al., 2025; Song et al., 2025; Guo et al., 2025b) and possibly unhelpful (Uesato et al., 2022; Jia et al., 2025; Guo et al., 2025b). Second, RL techniques are sensitive to the choice of base LLMs, resulting in inconsistent fine-tuning performance across different models (Gandhi et al., 2025). Third, RL techniques have an inherent tendency to hack the reward function, leading to undesirable behaviors (Gao et al., 2023; Denison et al., 2024; Fu et al., 2025). Fourth, RL fine-tuning is often unstable across multiple runs even with the same parametric setup, increasing the cost of fine-tuning significantly (Choshen et al., 2020; Zhong et al., 2025).
Evolution Strategies (ES), a class of population-based zeroth-order optimization algorithms, is a possible alternative. ES has several unique advantages over RL in traditional control and gam-
∗Equal Contribution
† Project Lead, Correspondence to: Xin Qiu qiuxin.nju@gmail.com
‡Work done during internship at Cognizant AI Lab
ing problems: it is highly parallel, tolerates long-horizon rewards well, explores extensively, needs less computation (no backpropagation), and is robust to setup parameters (Salimans et al., 2017; Chrabaszcz et al., 2018; Conti et al., 2018). However, ES has received much less attention than RL during the LLM era. Standard ES works by searching and optimizing in the original parameter space directly, for which the dimension was no more than a few million in past implementations (Salimans et al., 2017; Zhang et al., 2017; Lehman et al., 2018; Lorenc & Neruda, 2025). It was assumed that if the model is very large, it is significantly more difficult and sample-inefficient to explore in parameter space compared to action-space (Vemula et al., 2019). The number of parameters in LLMs is usually on the order of billions, which may seem infeasible for ES to directly tackle. Existing workarounds include applying ES only to the last layer of the original model (Toledano-Lopez ´ et al., 2022), using ES to fine-tune a lower-dimensional adapter (Jin et al., 2024), and searching in action space as in standard RL (Huang et al., 2025). Directly searching in the full parameter space of LLMs has remained a daunting challenge.
This paper is aimed at meeting this challenge. For the first time, ES is scaled to multi-billionparameter search spaces, by searching directly over the full parameter space of LLMs in fine-tuning tasks. The approach is based on a memory-efficient implementation of an algorithmically simplified ES variant, with support for parallelization within and across GPUs. Performance is compared with state-of-the-art (SOTA) RL methods in fine-tuning various LLMs in a standard reasoning benchmark task, and behavioral differences from RL are analyzed in terms of fine-tuning for conciseness. This version of ES was able to search directly over billions of parameters, and exhibit surprisingly good fine-tuning performance compared to RL methods in multiple aspects:
- ES only needs response-level rewards, making it a perfect fit for fine-tuning on reasoning tasks that have only sparse long-horizon outcome rewards. In particular, ES obtained significantly better fine-tuned models than RL in the Countdown task with such rewards
- Counterintuitively, even though ES explores in the parameter space with billions of parameters, it is more sample efficient than RL methods that explore in the action space, which is much smaller. Further, ES was able to find good solutions with a population size of only 30. As a comparison, previous ES implementations (Salimans et al., 2017; Zhang et al., 2017; Lehman et al., 2018; Lorenc & Neruda, 2025) utilized a population size of 10,000 or more with much smaller models (i.e. millions of parameters or less).
- ES is significantly more robust than RL across different LLMs. While RL fine-tuning failed on some LLMs, ES provided good fine-tuning for all of them. ES benefits from its exploration in parameter space, making it less sensitive to initial states of the LLMs.
- Whereas RL tends to hack the reward function if no other penalty is added, ES consistently maintains reasonable behaviors during fine-tuning. The main reason is that ES optimizes a solution distribution (Lehman et al., 2018), which is more difficult to hack, while RL optimizes a single solution.
- ES's behavior is more consistent than RL's across different runs. This property can significantly reduce expected cost of fine-tuning.
- Fine-tuning with ES is based on inference, and therefore no backpropagation calculations are needed. A significant amount of GPU memory can therefore be saved (Malladi et al., 2023).
The study reported in this paper serves as a first step in demonstrating the potential of ES for finetuning LLMs. The surprising and counterintuitive findings motivates further work scaling up ES to larger LLM fine-tuning tasks. Given the unique advantages over the state of the art, ES opens up new opportunities in parameter-space exploration, outcome-only fine-tuning, and large-scale distributed post-training.
2 RELATED WORK
Evolution Strategies (ES, Rechenberg, 1973; Schwefel, 1977) are a class of evolutionary algorithms (EAs) for solving numerical optimization problems. The main idea is to sample a population of solutions through perturbations, then recombine the perturbed solutions based on their fitness values to form the population for the next generation. This process repeats until a termination condition is triggered, e.g., the maximum number of generations is reached. Among the different variants of ES, CMA-ES (Hansen & Ostermeier, 2001), which utilizes a multivariate Gaussian distribution with full covariance matrix to sample the population, and natural ES (Wierstra et al., 2008; 2014), which uses natural gradient to guide the search, are two popular methods for traditional optimization problems. Although ES has long been used to evolve parameters of neural networks (NNs), (Igel, 2003), Salimans et al. (2017) were the first to scale the approach up to deep learning networks. Comparable performance to RL methods in control and gaming environments was observed, and several unique advantages of ES highlighted. This seminal work paved the way for several followup studies. Zhang et al. (2017) used ES to optimize a convolutional NN with around three million parameters. They found that with a large enough population size, ES can approximate the performance of traditional stochastic gradient descent (SGD). Lehman et al. (2018) further optimized an NN comprising nearly 167,000 parameters with both ES and a traditional finite-difference (FD) gradient estimator. Because ES optimizes the average reward for the entire population, whereas FD optimizes the reward for a single solution, it obtained models that were more robust to parameter perturbations. Lorenc & Neruda (2025) applied ES to optimize decision transformers in RL environments, and observed promising results for model sizes up to around 2.5 million parameters. In a related study, another traditional EA, namely genetic algorithm (GA) with mutations only, was extended to a high-dimensional space (Such et al., 2017). Encouraging results were observed in different types of models with up to around four million parameters (Such et al., 2017; Risi & Stanley, 2019). However, although these studies were promising, the scale of these implementations was still significantly less than the size of current LLMs.
Synergies between Evolutionary Algorithms (EAs) and LLMs have received increasing attention in recent years (Wang et al., 2025; Wu et al., 2025). Popular research directions include EAs for prompt optimization (Sun et al., 2022b;a; Zhao et al., 2023; Guo et al., 2024), utilizing LLMs as evolutionary operators (Meyerson et al., 2024; Lehman et al., 2024; Romera-Paredes et al., 2024; Novikov et al., 2025), and merging LLMs through evolution (Du et al., 2024; Akiba et al., 2025). Applying EAs to optimize billions of parameters in LLMs is generally perceived to be intractable, but a few studies have been successful at a smaller scale. For example, Toledano-Lopez et al. (2022) ´ fine-tuned the last layer (with 325 parameters) of an mT5-based transformer via CMA-ES. Jin et al. (2024) optimized the low-rank adapter parameters (with dimensionality up to 1600) using CMA-ES and the Fireworks algorithm. Sanchez Carmona et al. (2024) applied a GA to fine-tune around 9.5 million parameters of a transformer encoder, though poorer performance than the traditional Adam optimizer was observed. Huang et al. (2025) proposed a hybrid algorithm that performs exploration in action space instead of parameter space, and it was only used in the final epoch of supervised fine-tuning (SFT). The work in this paper significantly extends this prior research by successfully scaling ES to search in the billions of parameters of LLMs, leading to surprisingly good fine-tuning performance.
Fine-tuning using RL is a critical step during the training of many landmark LLMs (Ouyang et al., 2022; Bai et al., 2022; Shao et al., 2024; Guo et al., 2025a;b). Proximal Policy Optimization (PPO; Schulman et al., 2017) and Group Relative Policy Optimization (GRPO; Shao et al., 2024) are the two predominant methods. PPO introduces a clipped surrogate objective to limit the update scale in each step with respect to the old policy, and it usually works with a value model in an actor-critic manner. GRPO simplifies the pipeline of PPO by replacing the value model with group advantage, which is calculated based on direct evaluations of multiple responses. As discussed in Section 1, in the context of LLM fine-tuning, these methods struggle with several fundamental limitations, including the dilemma in handling long-horizon reward (Vemula et al., 2019; Salimans et al., 2017; Zhang et al., 2025; Song et al., 2025; Uesato et al., 2022; Jia et al., 2025; Guo et al., 2025b), sensitivity to base LLMs (Gandhi et al., 2025), tendency to hack reward (Gao et al., 2023; Denison et al., 2024; Fu et al., 2025), and instability across runs (Choshen et al., 2020; Zhong et al., 2025). ES inherently avoids these limitations, leading to better fine-tuning performance.
Existing RL fine-tuning methods are overwhelmingly based on action-space exploration. Parameter space exploration has received much less attention, though some such studies do exist (Ruckstieß ¨ et al., 2008; Sehnke et al., 2010; Ruckstieß et al., 2010; Plappert et al., 2018). Although promising ¨ performance was observed in problems with sparse rewards, the scale of the tested models was far smaller than that of LLMs. Vemula et al. (2019) performed a theoretical analysis of different exploration strategies, and found that the complexity of the parameter space exploration increased quadratically with the number of parameters, whereas the complexity of action space exploration depended
Algorithm 1 Basic ES Algorithm
Require: Pretrained LLM with initial parameters \theta_0, reward function R(\cdot), total iterations T, population size N, noise scale \sigma, learning rate \alpha.
1: for t=1 to T do \qquad \qquad \triangleright outer ES iterations 2: for n=1 to N do 3: Sample noise \varepsilon_n \sim \mathcal{N}(0, \mathbf{I}) 4: Compute reward for perturbed parameters R_n = R(\boldsymbol{\theta}_{t-1} + \sigma \cdot \boldsymbol{\varepsilon}_n) 5: end for 6: Normalize R_n Update model parameters as \boldsymbol{\theta}_t \leftarrow \boldsymbol{\theta}_{t-1} + \alpha \cdot \frac{1}{N} \sum_{n=1}^N R_n \boldsymbol{\varepsilon}_n 8: end for
on action dimensionality quadratically and horizon length of the reward quartically. Based on the classical SPSA optimization method (Spall, 1992), Malladi et al. (2023) proposed a zeroth-order optimizer MeZO that directly worked in parameter space for fine-tuning LLMs. MeZO significantly reduced memory requirements, but its fine-tuning performance was no better than other baselines. In contrast, the ES implementation in this paper performs exploration in multi-billion-parameter search spaces, and outperforms all baselines.
3 METHOD
This section introduces the basic algorithmic structure of ES, followed by a detailed description of its implementation for LLM fine-tuning.
3.1 Basic ES Algorithm
The ES implementation in this paper is an algorithmically simplified variant of natural evolution strategies (NES) (Wierstra et al., 2008; 2014). The overall design is similar to OpenAI ES (Salimans et al., 2017), which simplified NES with fixed covariance for perturbation noise.
Given a pretrained LLM with initial parameters $\theta_0$ and a target reward function $R(\cdot)$ , the task is to fine-tune the parameters so that the reward function is optimized (Algorithm 1). In each iteration, N perturbed models are sampled by adding random Gaussian noise $\varepsilon_n$ to their parameters. The noise is i.i.d. in each dimension of the parameter space, and it is scaled by the hyperparameter $\sigma$ . The perturbed models are evaluated to obtain their reward scores $R_n$ . The final update of the model parameters aggregates the sampled perturbations by weighting them using their normalized reward scores. The standard update equation $\theta_t \leftarrow \theta_{t-1} + \alpha \cdot \frac{1}{\sigma} \frac{1}{N} \sum_{n=1}^N R_n \varepsilon_n$ is simplified to $\theta_t \leftarrow \theta_{t-1} + \alpha \cdot \frac{1}{\sigma} \sum_{n=1}^N R_n \varepsilon_n$ by digesting the term $\frac{1}{\sigma}$ into the learning rate $\alpha$ .
To improve scalability, a number of modifications to this basic algorithm were made as detailed in the next section.
3.2 IMPLEMENTATION DETAILS
Algorithm 2, the actual implementation of ES for this paper, expands on the above algorithm in seven ways:
(1) Noise retrieval with random seeds: Similar to Salimans et al. (2017); Such et al. (2017), only the random seeds are stored to reduce GPU memory usage. The perturbation noise used during sampling can be retrieved exactly by resetting the random number generator with specific random seeds. (2) Parallel evaluations: In each iteration, the perturbed models can be evaluated fully in parallel by assigning a separate random seed to each process. (3) Layer-level in-place perturbation and restoration: To reduce the peak GPU memory usage, the model parameters are perturbed in-place layer by layer, with corresponding random seeds archived. After evaluation of the perturbed model, the model parameters are restored by subtracting the same noise perturbations using the archived random seeds. For each evaluation process, apart from the model parameters, the only additional memory needed is to store a tensor the size of a layer temporarily. (4) Reward normalization:
Algorithm 2 ES Implementation for LLM Fine-Tuning
Require: Pretrained LLM with initial parameters $\theta_0$ , reward function $R(\cdot)$ , total iterations T, population size N, noise scale $\sigma$ , learning rate $\alpha$ , number of parallel process P.
1: Create P processes, each instantiates a model with the same initial parameters $\theta_0$ , with one process as the main process
2: for t = 1 to T do
▷ ES iterations
Sample N random seeds s_1, s_2, \ldots, s_N
3:
4:
Assign random seeds to P processes
5:
for n=1 to N do
For the process handling s_n, reset its random number generator using random seed s_n
6:
> perturbation within current process
7:
for each LLM layer do
Sample noise \varepsilon_{n,l} \sim \mathcal{N}(0, \mathbf{I}), which has the same shape as the lth layer's parameters
8:
9:
Perturb the lth layer's parameters in-place: \theta_{t-1,l} \leftarrow \theta_{t-1,l} + \sigma \cdot \varepsilon_{n,l}
10:
Compute reward for perturbed parameters R_n = R(\boldsymbol{\theta}_{t-1})
11:
12:
For the process handling s_n, reset its random number generator using random seed s_n
13:
for each LLM layer do
> restoration within current process
14:
Sample noise \varepsilon_{n,l} \sim \mathcal{N}(0, \mathbf{I}), which has the same shape as the lth layer's parameters
15:
Restore the lth layer's parameters in-place: \theta_{t-1,l} \leftarrow \theta_{t-1,l} - \sigma \cdot \varepsilon_{n,l}
16:
end for
17:
Normalize the reward scores by calculating the z-score for each R_n: Z_n = \frac{R_n - R_{\text{mean}}}{R_{\text{std}}}, where R_{\text{mean}} and R_{\text{std}} are the mean and standard deviation of R_1, R_2, \ldots, R_N.
18:
19:
for n=1 to N do
in main process only
Reset current random number generator using random seed s_n
20:
21:
for each LLM layer do
Sample noise \varepsilon_{n,l} \sim \mathcal{N}(0, I), which has the same shape as the lth layer's parameters
22:
Update lth layer's parameters in-place as \theta_{t,l} \leftarrow \theta_{t-1,l} + \alpha \cdot \frac{1}{N} Z_n \varepsilon_{n,l}
23:
24:
end for
25:
end for
Update the model parameters of all processes to \theta_t
27: end for
The rewards of the perturbed models are normalized using z-score within each iteration, so that the normalized rewards for each iteration have a mean of 0 and standard deviation of 1. This normalization makes the reward scale consistent across iterations and tasks. (5) Greedy decoding: The perturbed models use greedy decoding to generate the responses for reward evaluations. As a result, the perturbed models are evaluated deterministically, so that all performance differences come from the exploration in parameter space instead of action space. (6) Decomposition of the parameter update: At the end of each iteration, the aggregated update of model parameters is performed inplace in a decomposed manner, gradually adding up layer by layer and seed by seed, significantly reducing the peak GPU memory needed. (7) Learning rate digestion: The standard update equation $\theta_t \leftarrow \theta_{t-1} + \alpha \cdot \frac{1}{\sigma} \sum_{n=1}^{N} R_n \varepsilon_n$ is simplified to $\theta_t \leftarrow \theta_{t-1} + \alpha \cdot \frac{1}{N} \sum_{n=1}^{N} R_n \varepsilon_n$ by digesting the term $\frac{1}{\sigma}$ into the learning rate $\alpha$ , simplifying the computation and parametric setup.
In order to keep the algorithm simple, common enhancements in OpenAI ES Salimans et al. (2017) such as rank transformation of rewards (Wierstra et al., 2014), mirrored sampling (Sehnke et al., 2010), weight decay, and virtual batch normalization (Salimans et al., 2016) are not used, and neither are more advanced optimizers like Adam (Kingma & Ba, 2015). They can be included in to improve results in future work.
4 EMPIRICAL STUDIES
This section first compares the fine-tuning performance of ES, PPO and GRPO on a standard reasoning benchmark. After that, behavioral differences between ES and RL are investigated in fine-tuning for conciseness in the next section.
| Base Model | Original | ES (ours) | |||
|---|---|---|---|---|---|
| PPO | GRPO (8) | GRPO (30) | |||
| Qwen-2.5-0.5B-Instruct | 0.1 | 0.3 | 0.3 | 0.5 | 14.4 |
| Qwen-2.5-1.5B-Instruct | 0.7 | 14.2 | 13.9 | 14.8 | 37.3 |
| Qwen-2.5-3B-Instruct | 10.0 | 20.1 | 30.9 | 32.5 | 60.5 |
| Qwen-2.5-7B-Instruct | 31.2 | 55.1 | 54.2 | 52.8 | 66.8 |
| LLaMA-3.2-1B-Instruct | 0.4 | 11.2 | 14.5 | 13.0 | 16.8 |
| LLaMA-3.2-3B-Instruct | 3.2 | 35.3 | 39.4 | 38.8 | 51.6 |
| LLaMA-3.1-8B-Instruct | 8.1 | 42.8 | 49.9 | 51.3 | 61.2 |
Table 1: Accuracy (%) on the Countdown task across model families, sizes, and fine-tuning algorithms. Different model families are shaded for clarity; Original refers to directly evaluating the base model without any fine-tuning, and GRPO (8) and GRPO (30) indicate group sizes of 8 and 30. The same hyperparameters were used for all ES runs; a separate grid search for the best hyperparameters was run for each RL experiment.
4.1 PERFORMANCE IN THE COUNTDOWN TASK
Fine-tuning performance was measured in the Countdown task (Pan et al., 2025; Goodfellow et al., 2016), a symbolic reasoning benchmark, showing that ES is accurate and sample efficent across different kinds and sizes of LLMs, even when the RL approaches is not.
Countdown task. The Countdown task (Pan et al., 2025; Goodfellow et al., 2016) requires constructing an arithmetic expression from a given set of numbers using basic operations (+, −, ×, ÷) to match a target value. For instance, the target 950 can be obtained from {100, 50, 6, 3} with 100 × (6 + 3) + 50 = 950). This constitutes a compact test of constrained symbolic reasoning, i.e. an important use case for fine-tuning.
Experimental Setup. A single fixed set of hyperparameters was used for all ES experiments. For RL, a separate hyperparameter sweep was done for each experiment. RL methods turned out sensitive to hyperparameters, in particular the KL-divergence penalty coefficient β and learning rate α, and did not make much progress if they were not set precisely. To mitigate this issue, for each model, a small grid of β and α values were tested and the best-performing configuration selected (further details are provided in Table 3 in the Appendix A.1). This approach makes the comparison conservative with respect to ES, but it also highlights its robustness.
ES improves upon PPO and GRPO across all tested models. Previously, Gandhi et al. (2025) found that RL does not generalize well across models on the Countdown task. Table 1 confirms this result, and also demonstrates that ES does not have this problem. With each model in the Qwen2.5 family (0.5B–7B) and the LLaMA3 family (1B–8B), ES substantially improved over both PPO and GRPO, often by a large margin. Averaged across all models, ES improves over the base model by 36.4%, compared to 17.9% for PPO and 21.3% for GRPO with group size N = 8 and 21.4% for group size N = 30 (see Figure 5 in Appendix A.4 for a model-wise visual comparison). These results demonstrate that ES scales effectively across different model types and sizes, and does so significantly better than RL.
ES is more sample efficient than RL. Surprisingly, even when searching in a space with billions of parameters, ES is more sample efficient than the RL methods. The experiments reported in Table 1 were all run with the same total number of training sample evaluations (each training sample is one Countdown question). Figure 6 in Appendix A.4 further shows the learning curves; to reach the same level of fine-tuning performance as RL, ES needs less than 20% of the training sample evaluations in most cases. This observation is different from the that of Salimans et al. (2017), who found worse sample efficiency compared to RL. One critical factor is the population size N; the experiments in this paper had N = 30, whereas Salimans et al. (2017) used N = 10, 000, which may explain the difference.
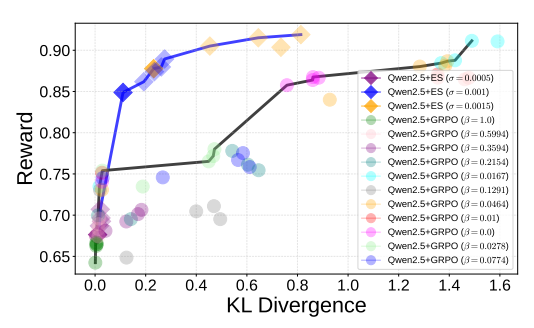
Figure 1: Mean conciseness reward and mean KL divergence from the base model for each fine-tuning checkpoint across different learning parameters. The Pareto front of ES (blue line) is higher and to the left of the GRPO Pareto front (black line) models, indicating that it found better tradeoffs. ES discovers these solutions without any KL divergence penalty, suggesting that it represents a distinctly different fine-tuning mechanism from the GRPO.
ES is effective on smaller models. Prior work on DeepSeek-R1 (Guo et al., 2025b) and Tiny-Zero (Pan et al., 2025) pointed out a key limitation of PPO and GRPO: they require sufficient large base models to improve. For instance, Pan et al. (2025) note that "for Qwen2.5-0.5B base, we know it fails to learn reasoning." Surprisingly, ES overcomes this limitation. As shown in Table 1, while PPO and GRPO indeed obtain only 0.3% accuracy on that model, ES boosts accuracy to 14.4%, thus eliciting reasoning even from the smallest-scale base model. This performance difference demonstrates the benefit of parameter-space exploration in ES: while RL cannot find better actions from the limited initial model to bootstrap learning, ES modifies the model directly by adding perturbations in parameter space, possibly creating better models to facilitate further exploration. These results highlight a distinct advantage of ES: it is able to improve behavior even with smaller, weaker base models, thus expanding the scope of fine-tuning.
4.2 BEHAVIORAL DIFFERENCES BETWEEN ES AND RL IN FINE-TUNING FOR CONCISENESS
In order to characterize the different approaches that ES and RL take, they were used to fine-tune Qwen-2.5-7B Instruct, towards more concise responses in question-answering. That is, fine-tuning was rewarded based on how concise the answers were, but not directly rewarded for its question-answering performance. In this setup, it was possible to analyze not only whether fine-tuning was effective, but also how it was achieved, including what its side effects were.
Conciseness task. For conciseness fine-tuning, a dataset of prompts $\mathcal{D}=\{x_1,...,x_K\}$ , with a set of verifiable solutions $\{s_1,...,s_K\}$ , i.e. shortest possible correct answers, was used. For example, for the prompt "Name one primary color", possible shortest verifiable solution used is "Red". Following this approach, for each prompt $x\in\mathcal{D}$ , the model was encouraged to generate a concise response y. To fine-tune the model to generate concise responses, a reward computed using the absolute length difference between the generated response y and the corresponding verified solution $s_k$ was given to the model for each prompt $x_k$ . The reward function R for conciseness was defined as $R = -|\mathrm{len}(y) - \mathrm{len}(s_k)|$ , where $\mathrm{len}(\cdot)$ denotes the string length.
Behavior metrics. Behavior of the fine-tuned models was measured in two ways: the mean conciseness reward and the mean KL divergence from the base model (after Rafailov et al., 2023). KL divergence is useful as a proxy for the preservation of the base model's behavior. It correlates strongly with the question-answering performance of the model, but also conveys more information, i.e. the extent of the fine-tuning changes. A low KL divergence thus suggests that the fine-tuned model has not forgotten capabilities learned during pre-training. Further, as KL divergence increases, these capabilities are likely to break. Therefore, fine-tuning behavior can be characterized using the tradeoffs between reward and KL divergence. To compute the metrics, each fine-tuned model was evaluated on a set of held-out test prompts, with 20 responses sampled per prompt. The reward was computed using the model-generated response and the verifiable solution provided in the test dataset. The KL divergence between a fine-tuned model $\theta_{\rm FT}$ and a base model $\theta_{\rm BASE}$ for a given prompt x and corresponding response y was approximated following Schulman (2020) as
$$KL[\theta_{FT} \| \theta_{BASE}] = \frac{\theta_{BASE}(y_{i,t} | x, y_{i, < t})}{\theta_{FT}(y_{i,t} | x, y_{i, < t})} - \log \frac{\theta_{BASE}(y_{i,t} | x, y_{i, < t})}{\theta_{FT}(y_{i,t} | x, y_{i, < t})} - 1. \tag{1} $$
ES discovers a dominant Pareto front. Similarly to Rafailov et al. (2023), a Pareto frontier analysis was used to compare ES and GRPO, with mean reward and mean KL divergence as the metrics
| Model | $\boldsymbol{eta}$ | $\alpha$ | $\sigma$ | Reward ↑ | KL↓ |
|---|---|---|---|---|---|
| Qwen-2.5-7B+GRPO | 0.0 | $5 \times 10^{-6}$ | X | $0.867 \pm 0.054^*$ | $0.861 \pm 0.614^*$ |
| Qwen-2.5-7B+GRPO | 0.01 | $5 \times 10^{-6}$ | X | $0.871 \pm 0.060^*$ | $1.354 \pm 0.873^*$ |
| Qwen-2.5-7B+GRPO | 0.0167 | $5 \times 10^{-6}$ | X | $0.911 \pm 0.038$ | $1.591 \pm 0.811$ |
| Qwen-2.5-7B+GRPO | 0.0464 | $5 \times 10^{-6}$ | X | $0.881 \pm 0.062$ | $1.384 \pm 1.187$ |
| Qwen-2.5-7B+ES | X | 0.0005 | 0.001 | $0.889 \pm 0.004$ | $0.274 \pm 0.096$ |
| Qwen-2.5-7B+ES | X | 0.00075 | 0.0015 | $0.919 \pm 0.008$ | $0.813 \pm 0.212$ |
Table 2: Behavior or GRPO and ES in terms of mean conciseness reward and mean KL divergence. The label * indicates cases where reward hacking was observed. Only models that did not hack the reward were included in the results.
(Figure 1). The experimental setup is described in Appendix A.1. The ES Pareto front is represented by a blue line on top and the GRPO Pareto front by the black line below. That is, ES produced better tradeoffs than GRPO, i.e. models with higher reward and lower KL divergence. The GRPO results were achieved only after augmenting the conciseness reward with a KL divergence penalty (weighted by a parameter $\beta$ ). Without it, fine-tuning resulted in excessive divergence and incorrect answers. Remarkably, ES achieved superior tradeoffs without any KL divergence penalty, suggesting that ES fine-tuning is based on discovering distinctly different kinds of solutions than GRPO. Appendix A.3 presents additional experiments with varying $\alpha$ and $\beta$ values, yielding similar conclusions.
ES is more robust against reward hacking. GRPO with $\beta = \{0.0, 0.01\}$ sometimes hacked the reward, that is, produced responses that were short but contain nonsensical symbols rather than words. By increasing the KL-penalty via higher $\beta$ values, reward hacking could be prevented. The optimal $\beta$ is likely to be problem specific and to require extensive search to find. In contrast, ES does not receive any feedback about the divergence of the fine-tuned model, and only seeks to optimize conciseness. Regardless, it did not exhibit any reward hacking, despite achieving mean reward comparable to GRPO with $\beta = \{0.0, 0.01\}$ . This result again suggests that ES finds a different way of optimizing the reward function.
ES fine-tuning is reliable across runs. Fine-tuning LLMs is computationally expensive, and it is therefore critical that it leads to consistent results across runs. Table 2 presents the mean and standard deviation of the conciseness reward and KL divergence across four independent runs after 1,000 iterations. A mean reward cut-off of > 0.85 was used to down-select hyperparameter combinations, ensuring that only the best ES and GRPO configurations were included in the analysis.
As shown in Table 2, ES achieved consistent conciseness rewards,indicated by a low reward standard deviation (0.004 and 0.008) over four runs with different random seeds. GRPO has $15.5\times$ higher standard deviation (0.041–0.062), suggesting that its results were much less consistent. The results on KL divergence were similar. For instance, while ES ( $\sigma=0.0015$ ) and GRPO ( $\beta=0.0167$ ) achieved similar mean rewards, GRPO exhibits a $1.95\times$ higher KL divergence mean and $3.83\times$ greater standard deviation. Similarly, while ES ( $\sigma=0.001$ ) achieves a slightly lower reward compared to GRPO ( $\beta=0.0167$ ), GRPO ( $\beta=0.0167$ ) has a $5.8\times$ higher KL divergence and a $8.44\times$ higher standard deviation. Thus, ES fine-tuning is more reliable than GRPO.
5 DISCUSSION AND FUTURE WORK
Exploration in parameter space plays a key role in the surprisingly good fine-tuning performance of ES. As discussed by Rückstieß et al. (2010) and Plappert et al. (2018), sampling noise in parameter space ensures that the entire action trajectory, i.e., the sequence of tokens, only depends on one single sampling, leading to significantly lower variance in rollouts, i.e., in response generation. As a result, gradient estimation is more reliable and convergence is more stable. In contrast, action space exploration in RL injects noise at every step, i.e., at each token position, resulting in high variance in the sequence generation. The behavior of RL therefore is much less reliable than ES, as was seen in Table 2. Moreover, step-wise exploration in action space promotes reward hacking by increasing
the chance of sampling a single hacking action. One example is the nonsensical symbol sampled during RL that can hack the conciseness reward.
Another key difference between ES and RL is that ES intrinsically optimizes a solution distribution (Lehman et al., 2018), while RL optimizes a single solution. This property makes it more difficult for ES to hack the reward since a single hacked solution usually does not have a high-quality solution distribution around it. This property also results in solutions that are more robust to noisy perturbations in parameter space (Lehman et al., 2018), making them more robust to adversarial attacks and less likely to be compromised in other follow-up fine-tuning tasks (Chen et al., 2025).
In the experiments in this paper, extensive hyperparameter tuning was performed for RL methods, resulting in specific RL hyperparameters for different model sizes and families. In comparison, ES was found to be less sensitive to hyperparameters, and the same set of hyperparameters was used for all experiments. While there are many common enhancements for ES (Salimans et al., 2017), none were used in the experiments so that the power of vanilla ES could be clearly demonstrated. Thus, it may be possible to improve the results with more extensive hyperparameter tuning and other enhancements.
One counterintuitive result is that the ES implementation only needs a population of 30 to effectively optimize billions of parameters. In contrast, previous work (Salimans et al., 2017; Zhang et al., 2017; Lehman et al., 2018; Lorenc & Neruda, 2025) used populations of 10,000 or more for models with millions or fewer parameters. An interesting future direction is to analyze how such small populations are possible. Perhaps this is related to the observed low intrinsic dimensionality of LLMs (Aghajanyan et al., 2021). Another promising direction is to use ES to perform unsupervised fine-tuning based on internal behaviors of LLMs, such as confidence calculated based on semantic entropy and semantic density (Qiu & Miikkulainen, 2024; Farquhar et al., 2024). Such fine-tuning cannot be done with RL, since action space exploration does not change the internal representations of LLMs (that is, each action sampling is generated via output distribution without changing the internal parameters). In a broader sense, since ES does not need process rewards during exploration, it may be a necessary ingredient for superintelligence (Mucci & Stryker, 2023), which would be difficult to achieve by supervised learning using process guidance from human data. Massive parallelization of ES will speed up exploration by distributing the computations across GPU machines or even data centers.
An important question is: what are the underlying computational mechanisms that make ES and RL behave so differently? While this question requires significant further work, a possible hypothesis emerges from the experiments in this paper. Many fine-tuning objectives, like conciseness and the Countdown task, are long-horizon outcome-only objectives. The reward signal is jagged, making it difficult to navigate with gradient-based post-training methods. RL and ES both provide workarounds via effective noise injection to "smooth out" the jagged reward landscape. In the case of RL, noise is introduced from Monte-Carlo sampling of each token during a rollout, averaged over many rollouts, which effectively smooths the sampling process but does not necessarily guarantee that the reward landscape is smooth in parameter space. RL's gradient estimation therefore has a high-variance, and its signal-to-noise ratio becomes worse with longer sequences and sharper policies (i.e. those with lower entropy), and therefore prone to undesirable outcomes such as reward hacking.
In contrast, ES injects noise directly into the parameter space via explicit Gaussian convolution, which effectively smooths out the jagged reward landscape. As a result, it provides a more stable way of exploring the landscape, leading to more consistent, efficient, and robust optimization (as observed in the experiments and in Appendix A.5). Moreover, the larger the models and the sharper the policies, the more jagged the reward landscapes; therefore, ES is likely to have an advantage in fine-tuning them. Direct evidence for this hypothesis still needs to be obtained, but it provides a plausible mechanistic explanation, and a direction for future work. Eventually such work could result in better fine-tuning methods, as well as an improved understanding of LLMs in general.
6 CONCLUSION
This paper introduces and evaluates a new approach to fine-tuning LLMs, based on scaling up ES to billions of dimensions. The approached performed significantly better than the standard RL finetuning in the Countdown task, which has sparse long-horizon rewards. ES was found to be more sample efficient, less sensitive to hyperparameter setup, and to achieve consistently better results across multiple LLMs. Further empirical studies on fine-tuning for conciseness revealed that ES is less likely to hack the reward, and behaves reliably across multiple runs. The mechanisms underlying these differences still need to be characterized, but a plausible hypothesis is that the exploration in ES is better suited for the jagged reward landscapes in large models. ES therefore constitutes a promising alternative to RL in fine-tuning LLMs.
REPRODUCIBILITY STATEMENT
The experimental and parametric setup is provided in full details in Appendix A.1 for reproducing all the experimental results reported in this paper. Source codes for generating the experimental results are provided at: https://github.com/VsonicV/es-fine-tuning-paper.
REFERENCES
Josh Achiam et al. GPT-4 technical report. arXiv:2303.08774, 2024.
- Armen Aghajanyan, Sonal Gupta, and Luke Zettlemoyer. Intrinsic dimensionality explains the effectiveness of language model fine-tuning. In Chengqing Zong, Fei Xia, Wenjie Li, and Roberto Navigli (eds.), Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pp. 7319–7328, Online, August 2021. Association for Computational Linguistics. doi: 10.18653/v1/2021.acl-long.568. URL https://aclanthology.org/2021. acl-long.568/.
- AI@Meta. Llama 3 model card, 2024. URL https://github.com/meta-llama/llama3/ blob/main/MODEL\_CARD.md.
- Takuya Akiba, Makoto Shing, Yujin Tang, Qi Sun, and David Ha. Evolutionary optimization of model merging recipes. Nature Machine Intelligence, 7(2):195–204, 2025. doi: 10.1038/ s42256-024-00975-8. URL https://doi.org/10.1038/s42256-024-00975-8.
- Anthropic. Introducing Claude 4, 2025. URL https://www.anthropic.com/news/ claude-4.
- Yuntao Bai, Andy Jones, Kamal Ndousse, Amanda Askell, Anna Chen, Nova DasSarma, Dawn Drain, Stanislav Fort, Deep Ganguli, Tom Henighan, Nicholas Joseph, Saurav Kadavath, Jackson Kernion, Tom Conerly, Sheer El-Showk, Nelson Elhage, Zac Hatfield-Dodds, Danny Hernandez, Tristan Hume, Scott Johnston, Shauna Kravec, Liane Lovitt, Neel Nanda, Catherine Olsson, Dario Amodei, Tom Brown, Jack Clark, Sam McCandlish, Chris Olah, Ben Mann, and Jared Kaplan. Training a helpful and harmless assistant with reinforcement learning from human feedback. arXiv:2204.05862, 2022. URL https://arxiv.org/abs/2204.05862.
- Huanran Chen, Yinpeng Dong, Zeming Wei, Yao Huang, Yichi Zhang, Hang Su, and Jun Zhu. Understanding pre-training and fine-tuning from loss landscape perspectives. arXiv:2505.17646, 2025. URL https://arxiv.org/abs/2505.17646.
- Leshem Choshen, Lior Fox, Zohar Aizenbud, and Omri Abend. On the weaknesses of reinforcement learning for neural machine translation. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=H1eCw3EKvH.
- Patryk Chrabaszcz, Ilya Loshchilov, and Frank Hutter. Back to basics: benchmarking canonical evolution strategies for playing atari. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, IJCAI'18, pp. 1419–1426. AAAI Press, 2018. ISBN 9780999241127.
-
Edoardo Conti, Vashisht Madhavan, Felipe Petroski Such, Joel Lehman, Kenneth Stanley, and Jeff Clune. Improving exploration in evolution strategies for deep reinforcement learning via a population of novelty-seeking agents. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (eds.), Advances in Neural Information Processing Systems, volume 31. Curran Associates, Inc., 2018.
-
Carson Denison, Monte MacDiarmid, Fazl Barez, David Duvenaud, Shauna Kravec, Samuel Marks, Nicholas Schiefer, Ryan Soklaski, Alex Tamkin, Jared Kaplan, Buck Shlegeris, Samuel R. Bowman, Ethan Perez, and Evan Hubinger. Sycophancy to subterfuge: Investigating reward-tampering in large language models. arXiv:2406.10162, 2024. URL https://arxiv.org/abs/ 2406.10162.
- Guodong Du, Jing Li, Hanting Liu, Runhua Jiang, Shuyang Yu, Yifei Guo, Sim Kuan Goh, and Ho-Kin Tang. Knowledge fusion by evolving weights of language models. In Lun-Wei Ku, Andre Martins, and Vivek Srikumar (eds.), Findings of the Association for Computational Linguistics: ACL 2024, pp. 11727–11742, Bangkok, Thailand, August 2024. Association for Computational Linguistics. doi: 10.18653/v1/2024.findings-acl.698. URL https://aclanthology.org/ 2024.findings-acl.698/.
- Sebastian Farquhar, Jannik Kossen, Lorenz Kuhn, and Yarin Gal. Detecting hallucinations in large language models using semantic entropy. Nature, 630(8017):625–630, 2024.
- Jiayi Fu, Xuandong Zhao, Chengyuan Yao, Heng Wang, Qi Han, and Yanghua Xiao. Reward shaping to mitigate reward hacking in RLHF. arXiv:2502.18770, 2025. URL https: //arxiv.org/abs/2502.18770.
- Kanishk Gandhi, Ayush K Chakravarthy, Anikait Singh, Nathan Lile, and Noah Goodman. Cognitive behaviors that enable self-improving reasoners, or, four habits of highly effective STars. In Second Conference on Language Modeling, 2025. URL https://openreview.net/ forum?id=QGJ9ttXLTy.
- Leo Gao, John Schulman, and Jacob Hilton. Scaling laws for reward model overoptimization. In Andreas Krause, Emma Brunskill, Kyunghyun Cho, Barbara Engelhardt, Sivan Sabato, and Jonathan Scarlett (eds.), Proceedings of the 40th International Conference on Machine Learning, volume 202 of Proceedings of Machine Learning Research, pp. 10835–10866. PMLR, 23–29 Jul 2023. URL https://proceedings.mlr.press/v202/gao23h.html.
- Ian Goodfellow, Yoshua Bengio, Aaron Courville, and Yoshua Bengio. Deep learning, volume 1. MIT Press, 2016.
- Google. Gemini 2.5: Pushing the frontier with advanced reasoning, multimodality, long context, and next generation agentic capabilities., 2025. URL https://storage.googleapis.com/ deepmind-media/gemini/gemini\_v2\_5\_report.pdf.
- Daya Guo et al. Deepseek-r1: Incentivizing reasoning capability in llms via reinforcement learning. arXiv:2501.12948, 2025a. URL https://arxiv.org/abs/2501.12948.
- Daya Guo et al. Deepseek-r1 incentivizes reasoning in llms through reinforcement learning. Nature, 645(8081):633–638, 2025b. doi: 10.1038/s41586-025-09422-z. URL https://doi.org/ 10.1038/s41586-025-09422-z.
- Qingyan Guo, Rui Wang, Junliang Guo, Bei Li, Kaitao Song, Xu Tan, Guoqing Liu, Jiang Bian, and Yujiu Yang. Connecting large language models with evolutionary algorithms yields powerful prompt optimizers. In The Twelfth International Conference on Learning Representations, 2024. URL https://openreview.net/forum?id=ZG3RaNIsO8.
- Nikolaus Hansen and Andreas Ostermeier. Completely derandomized self-adaptation in evolution strategies. Evolutionary Computation, 9(2):159–195, 2001. doi: 10.1162/106365601750190398.
- Bo Huang, Yuxin Jiang, Mingyang Chen, Yi Wang, Hongyang Chen, and Wei Wang. When evolution strategy meets language models tuning. In Owen Rambow, Leo Wanner, Marianna Apidianaki, Hend Al-Khalifa, Barbara Di Eugenio, and Steven Schockaert (eds.), Proceedings of the 31st International Conference on Computational Linguistics, pp. 5333–5344, Abu Dhabi, UAE, January 2025. Association for Computational Linguistics. URL https://aclanthology. org/2025.coling-main.357/.
-
Christian Igel. Neuroevolution for reinforcement learning using evolution strategies. In Proceedings of the 2003 Congress on Evolutionary Computation, pp. 2588–2595, 2003.
-
Zeyu Jia, Alexander Rakhlin, and Tengyang Xie. Do we need to verify step by step? rethinking process supervision from a theoretical perspective. In Forty-second International Conference on Machine Learning, 2025. URL https://openreview.net/forum?id=4BfaPHfhJ0.
- Albert Q. Jiang, Alexandre Sablayrolles, Antoine Roux, Arthur Mensch, Blanche Savary, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Emma Bou Hanna, Florian Bressand, Gianna Lengyel, Guillaume Bour, Guillaume Lample, Lelio Renard Lavaud, Lucile Saulnier, Marie- ´ Anne Lachaux, Pierre Stock, Sandeep Subramanian, Sophia Yang, Szymon Antoniak, Teven Le Scao, Theophile Gervet, Thibaut Lavril, Thomas Wang, Timoth ´ ee Lacroix, and William El Sayed. ´ Mixtral of experts. arXiv:2401.04088, 2024.
- Feihu Jin, Yifan Liu, and Ying Tan. Derivative-free optimization for low-rank adaptation in large language models. IEEE/ACM Trans. Audio, Speech and Lang. Proc., 32:4607–4616, October 2024. ISSN 2329-9290. doi: 10.1109/TASLP.2024.3477330. URL https://doi.org/10. 1109/TASLP.2024.3477330.
- Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In Yoshua Bengio and Yann LeCun (eds.), 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, 2015. URL http: //arxiv.org/abs/1412.6980.
- Ehsan Latif and Xiaoming Zhai. Fine-tuning chatgpt for automatic scoring. Computers and Education: Artificial Intelligence, 6:100210, 2024. ISSN 2666-920X. doi: https://doi.org/10.1016/ j.caeai.2024.100210. URL https://www.sciencedirect.com/science/article/ pii/S2666920X24000110.
- Joel Lehman, Jay Chen, Jeff Clune, and Kenneth O. Stanley. Es is more than just a traditional finite-difference approximator. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO '18, pp. 450–457, New York, NY, USA, 2018. Association for Computing Machinery. ISBN 9781450356183. doi: 10.1145/3205455.3205474. URL https://doi. org/10.1145/3205455.3205474.
- Joel Lehman, Jonathan Gordon, Shawn Jain, Kamal Ndousse, Cathy Yeh, and Kenneth O. Stanley. Evolution Through Large Models, pp. 331–366. Springer Nature Singapore, Singapore, 2024. ISBN 978-981-99-3814-8. doi: 10.1007/978-981-99-3814-8 11. URL https://doi.org/ 10.1007/978-981-99-3814-8\_11.
- Aixin Liu, Bei Feng, Bing Xue, Bingxuan Wang, Bochao Wu, Chengda Lu, Chenggang Zhao, Chengqi Deng, Chenyu Zhang, Chong Ruan, et al. Deepseek-v3 technical report. arXiv:2412.19437, 2024.
- Yong Liu, Zirui Zhu, Chaoyu Gong, Minhao Cheng, Cho-Jui Hsieh, and Yang You. Sparse meZO: Less parameters for better performance in zeroth-order LLM fine-tuning, 2025. URL https: //openreview.net/forum?id=4Kw4KAoVnx.
- Matya´s Lorenc and Roman Neruda. Utilizing evolution strategies to train transformers in reinforce- ˇ ment learning. arXiv:2501.13883, 2025. URL https://arxiv.org/abs/2501.13883.
- Sadhika Malladi, Tianyu Gao, Eshaan Nichani, Alex Damian, Jason D Lee, Danqi Chen, and Sanjeev Arora. Fine-tuning language models with just forward passes. In A. Oh, T. Naumann, A. Globerson, K. Saenko, M. Hardt, and S. Levine (eds.), Advances in Neural Information Processing Systems, volume 36, pp. 53038–53075. Curran Associates, Inc., 2023. URL https://proceedings.neurips.cc/paper\_files/paper/2023/ file/a627810151be4d13f907ac898ff7e948-Paper-Conference.pdf.
- Elliot Meyerson, Mark J. Nelson, Herbie Bradley, Adam Gaier, Arash Moradi, Amy K. Hoover, and Joel Lehman. Language model crossover: Variation through few-shot prompting. ACM Trans. Evol. Learn. Optim., 4(4), November 2024. doi: 10.1145/3694791. URL https://doi.org/ 10.1145/3694791.
-
Tim Mucci and Cole Stryker. What is artificial superintelligence?, 2023. URL https://www. ibm.com/think/topics/artificial-superintelligence.
-
Alexander Novikov, Ngan V ˆ u, Marvin Eisenberger, Emilien Dupont, Po-Sen Huang, Adam Zsolt ˜ Wagner, Sergey Shirobokov, Borislav Kozlovskii, Francisco J. R. Ruiz, Abbas Mehrabian, M. Pawan Kumar, Abigail See, Swarat Chaudhuri, George Holland, Alex Davies, Sebastian Nowozin, Pushmeet Kohli, and Matej Balog. AlphaEvolve: A coding agent for scientific and algorithmic discovery. arXiv:2506.13131, 2025. URL https://arxiv.org/abs/2506. 13131.
- Long Ouyang, Jeff Wu, Xu Jiang, Diogo Almeida, Carroll L. Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, John Schulman, Jacob Hilton, Fraser Kelton, Luke Miller, Maddie Simens, Amanda Askell, Peter Welinder, Paul Christiano, Jan Leike, and Ryan Lowe. Training language models to follow instructions with human feedback. In Proceedings of the 36th International Conference on Neural Information Processing Systems, NIPS '22, Red Hook, NY, USA, 2022. Curran Associates Inc. ISBN 9781713871088.
- Jiayi Pan, Junjie Zhang, Xingyao Wang, Lifan Yuan, Hao Peng, and Alane Suhr. Tinyzero. https://github.com/Jiayi-Pan/TinyZero, 2025. Accessed: 2025-01-24.
- Matthias Plappert, Rein Houthooft, Prafulla Dhariwal, Szymon Sidor, Richard Y. Chen, Xi Chen, Tamim Asfour, Pieter Abbeel, and Marcin Andrychowicz. Parameter space noise for exploration. In International Conference on Learning Representations, 2018. URL https: //openreview.net/forum?id=ByBAl2eAZ.
- Xin Qiu and Risto Miikkulainen. Semantic density: Uncertainty quantification for large language models through confidence measurement in semantic space. In Proceedings of the 38th Conference on Neural Information Processing Systems, 2024.
- Rafael Rafailov, Archit Sharma, Eric Mitchell, Stefano Ermon, Christopher D. Manning, and Chelsea Finn. Direct preference optimization: your language model is secretly a reward model. In Proceedings of the 37th International Conference on Neural Information Processing Systems, NIPS '23, Red Hook, NY, USA, 2023. Curran Associates Inc.
- I. Rechenberg. Evolutionsstrategie: Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Problemata (Stuttgart). Frommann-Holzboog, 1973. ISBN 9783772803741. URL https://books.google.com/books?id=-WAQAQAAMAAJ.
- Sebastian Risi and Kenneth O. Stanley. Deep neuroevolution of recurrent and discrete world models. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO '19, pp. 456–462, New York, NY, USA, 2019. Association for Computing Machinery. ISBN 9781450361118. doi: 10.1145/3321707.3321817. URL https://doi.org/10.1145/ 3321707.3321817.
- Bernardino Romera-Paredes, Mohammadamin Barekatain, Alexander Novikov, Matej Balog, M. Pawan Kumar, Emilien Dupont, Francisco J. R. Ruiz, Jordan S. Ellenberg, Pengming Wang, Omar Fawzi, Pushmeet Kohli, and Alhussein Fawzi. Mathematical discoveries from program search with large language models. Nature, 625(7995):468–475, 2024. doi: 10.1038/ s41586-023-06924-6. URL https://doi.org/10.1038/s41586-023-06924-6.
- Baptiste Roziere, Jonas Gehring, Fabian Gloeckle, Sten Sootla, Itai Gat, Xiaoqing Ellen Tan, ` Yossi Adi, Jingyu Liu, Romain Sauvestre, Tal Remez, Jer´ emy Rapin, Artyom Kozhevnikov, ´ Ivan Evtimov, Joanna Bitton, Manish Bhatt, Cristian Canton Ferrer, Aaron Grattafiori, Wenhan Xiong, Alexandre Defossez, Jade Copet, Faisal Azhar, Hugo Touvron, Louis Martin, Nicolas ´ Usunier, Thomas Scialom, and Gabriel Synnaeve. Code llama: Open foundation models for code. arXiv:2308.12950, 2024.
- Thomas Ruckstieß, Martin Felder, and J ¨ urgen Schmidhuber. State-dependent exploration for pol- ¨ icy gradient methods. In Walter Daelemans, Bart Goethals, and Katharina Morik (eds.), Machine Learning and Knowledge Discovery in Databases, pp. 234–249, Berlin, Heidelberg, 2008. Springer Berlin Heidelberg. ISBN 978-3-540-87481-2.
-
Thomas Ruckstieß, Frank Sehnke, Tom Schaul, Daan Wierstra, Yi Sun, and J ¨ urgen Schmidhuber. ¨ Exploring parameter space in reinforcement learning. Paladyn, 1(1):14–24, 2010. doi: 10.2478/ s13230-010-0002-4. URL https://doi.org/10.2478/s13230-010-0002-4.
-
Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. Improved techniques for training gans. In Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS'16, pp. 2234–2242, Red Hook, NY, USA, 2016. Curran Associates Inc. ISBN 9781510838819.
- Tim Salimans, Jonathan Ho, Xi Chen, Szymon Sidor, and Ilya Sutskever. Evolution strategies as a scalable alternative to reinforcement learning. arXiv:1703.03864, 2017. URL https: //arxiv.org/abs/1703.03864.
- Vicente Ivan Sanchez Carmona, Shanshan Jiang, and Bin Dong. How well can a genetic algorithm fine-tune transformer encoders? a first approach. In Shabnam Tafreshi, Arjun Akula, Joao˜ Sedoc, Aleksandr Drozd, Anna Rogers, and Anna Rumshisky (eds.), Proceedings of the Fifth Workshop on Insights from Negative Results in NLP, pp. 25–33, Mexico City, Mexico, June 2024. Association for Computational Linguistics. doi: 10.18653/v1/2024.insights-1.4. URL https://aclanthology.org/2024.insights-1.4/.
- John Schulman. Approximating kl divergence, 2020. URL http://joschu. net/blog/kl-approx. html, 2020.
- John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. arXiv:1707.06347, 2017. URL https://arxiv.org/abs/1707. 06347.
- Hans-Paul Schwefel. Numerische Optimierung von Computermodellen mittels der Evolutionsstrategie, volume 26. 01 1977. ISBN 9783764308766. doi: 10.1007/978-3-0348-5927-1.
- Frank Sehnke, Christian Osendorfer, Thomas Ruckstieß, Alex Graves, Jan Peters, and J ¨ urgen ¨ Schmidhuber. Parameter-exploring policy gradients. Neural Networks, 23(4):551–559, 2010. ISSN 0893-6080. doi: https://doi.org/10.1016/j.neunet.2009.12.004. URL https://www. sciencedirect.com/science/article/pii/S0893608009003220. The 18th International Conference on Artificial Neural Networks, ICANN 2008.
- Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Xiao Bi, Haowei Zhang, Mingchuan Zhang, Y. K. Li, Y. Wu, and Daya Guo. Deepseekmath: Pushing the limits of mathematical reasoning in open language models. arXiv:2402.03300, 2024. URL https: //arxiv.org/abs/2402.03300.
- Karan Singhal, Tao Tu, Juraj Gottweis, Rory Sayres, Ellery Wulczyn, Le Hou, Kevin Clark, Stephen Pfohl, Heather Cole-Lewis, Darlene Neal, Mike Schaekermann, Amy Wang, Mohamed Amin, Sami Lachgar, Philip Mansfield, Sushant Prakash, Bradley Green, Ewa Dominowska, Blaise Aguera y Arcas, Nenad Tomasev, Yun Liu, Renee Wong, Christopher Semturs, S. Sara Mahdavi, Joelle Barral, Dale Webster, Greg S. Corrado, Yossi Matias, Shekoofeh Azizi, Alan Karthikesalingam, and Vivek Natarajan. Towards expert-level medical question answering with large language models. arXiv:2305.09617, 2023.
- Mingyang Song, Zhaochen Su, Xiaoye Qu, Jiawei Zhou, and Yu Cheng. PRMBench: A finegrained and challenging benchmark for process-level reward models. In Wanxiang Che, Joyce Nabende, Ekaterina Shutova, and Mohammad Taher Pilehvar (eds.), Proceedings of the 63rd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pp. 25299–25346, Vienna, Austria, July 2025. Association for Computational Linguistics. ISBN 979-8-89176-251-0. doi: 10.18653/v1/2025.acl-long.1230. URL https://aclanthology. org/2025.acl-long.1230/.
- J.C. Spall. Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Transactions on Automatic Control, 37(3):332–341, 1992. doi: 10.1109/9.119632.
- Saksham Sahai Srivastava and Vaneet Aggarwal. A technical survey of reinforcement learning techniques for large language models. arXiv:2507.04136, 2025. URL https://arxiv.org/ abs/2507.04136.
-
Felipe Petroski Such, Vashisht Madhavan, Edoardo Conti, Joel Lehman, Kenneth O. Stanley, and Jeff Clune. Deep neuroevolution: Genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning. arXiv:1712.06567, 2017. URL https:// api.semanticscholar.org/CorpusID:5044808.
-
Tianxiang Sun, Zhengfu He, Hong Qian, Yunhua Zhou, Xuanjing Huang, and Xipeng Qiu. BBTv2: Towards a gradient-free future with large language models. In Yoav Goldberg, Zornitsa Kozareva, and Yue Zhang (eds.), Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, pp. 3916–3930, Abu Dhabi, United Arab Emirates, December 2022a. Association for Computational Linguistics. doi: 10.18653/v1/2022.emnlp-main.259. URL https://aclanthology.org/2022.emnlp-main.259/.
- Tianxiang Sun, Yunfan Shao, Hong Qian, Xuanjing Huang, and Xipeng Qiu. Black-box tuning for language-model-as-a-service. In Kamalika Chaudhuri, Stefanie Jegelka, Le Song, Csaba Szepesvari, Gang Niu, and Sivan Sabato (eds.), Proceedings of the 39th International Conference on Machine Learning, volume 162 of Proceedings of Machine Learning Research, pp. 20841–20855. PMLR, 17–23 Jul 2022b. URL https://proceedings.mlr.press/v162/sun22e. html.
- Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction. MIT Press, Cambridge, MA, 2nd edition, 2018.
- Orlando Grabiel Toledano-Lopez, Julio Madera, Hector Gonz ´ alez, Alfredo Sim ´ on-Cuevas, Thomas ´ Demeester, and Erik Mannens. Fine-tuning mt5-based transformer via cma-es for sentiment analysis. In Manuel Montes y Gomez, Julio Gonzalo, Francisco Rangel, Marco Casavantes, ´ Miguel Angel ´ Alvare Carmona, Gemma Bel Enguix, Hugo Jair Escalante, Larissa A. de Fre- ´ itas, Antonio Miranda-Escalada, Francisco J. Rodr´ıguez-Sanchez, Aiala Ros ´ a, Marco Anto- ´ nio Sobrevilla Cabezudo, Mariona Taule, and Rafael Valencia-Garc ´ ´ıa (eds.), Proceedings of the Iberian Languages Evaluation Forum (IberLEF 2022) co-located with the Conference of the Spanish Society for Natural Language Processing (SEPLN 2022), A Coruna, Spain, Septem- ˜ ber 20, 2022, volume 3202 of CEUR Workshop Proceedings. CEUR-WS.org, 2022. URL http://ceur-ws.org/Vol-3202/restmex-paper12.pdf.
- Hugo Touvron et al. Llama 2: Open foundation and fine-tuned chat models. arXiv:2307.09288, 2023.
- Jonathan Uesato, Nate Kushman, Ramana Kumar, Francis Song, Noah Siegel, Lisa Wang, Antonia Creswell, Geoffrey Irving, and Irina Higgins. Solving math word problems with processand outcome-based feedback. arXiv:2211.14275, 2022. URL https://arxiv.org/abs/ 2211.14275.
- Anirudh Vemula, Wen Sun, and J. Andrew Bagnell. Contrasting exploration in parameter and action space: A zeroth order optimization perspective. In Proceedings of 22nd International Conference on Artificial Intelligence and Statistics (AISTATS '19), March 2019.
- Chao Wang, Jiaxuan Zhao, Licheng Jiao, Lingling Li, Fang Liu, and Shuyuan Yang. When large language models meet evolutionary algorithms: Potential enhancements and challenges. Research, 8: 0646, 2025. doi: 10.34133/research.0646. URL https://spj.science.org/doi/abs/ 10.34133/research.0646.
- Daan Wierstra, Tom Schaul, Jan Peters, and Juergen Schmidhuber. Natural evolution strategies. In 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), pp. 3381–3387, 2008. doi: 10.1109/CEC.2008.4631255.
- Daan Wierstra, Tom Schaul, Tobias Glasmachers, Yi Sun, Jan Peters, and JA¼rgen Schmidhuber. ˜ Natural evolution strategies. Journal of Machine Learning Research, 15(27):949–980, 2014. URL http://jmlr.org/papers/v15/wierstra14a.html.
- Shijie Wu, Ozan Irsoy, Steven Lu, Vadim Dabravolski, Mark Dredze, Sebastian Gehrmann, Prabhanjan Kambadur, David Rosenberg, and Gideon Mann. Bloomberggpt: A large language model for finance. arXiv:2303.17564, 2023.
-
Xingyu Wu, Sheng-Hao Wu, Jibin Wu, Liang Feng, and Kay Chen Tan. Evolutionary computation in the era of large language model: Survey and roadmap. IEEE Transactions on Evolutionary Computation, 29(2):534–554, 2025. doi: 10.1109/TEVC.2024.3506731.
-
An Yang, Bowen Yu, Chengyuan Li, Dayiheng Liu, Fei Huang, Haoyan Huang, Jiandong Jiang, Jianhong Tu, Jianwei Zhang, Jingren Zhou, et al. Qwen2. 5-1m technical report. arXiv:2501.15383, 2025.
- Xingwen Zhang, Jeff Clune, and Kenneth O. Stanley. On the relationship between the openai evolution strategy and stochastic gradient descent. arXiv:1712.06564, 2017. URL https: //arxiv.org/abs/1712.06564.
- Zhenru Zhang, Chujie Zheng, Yangzhen Wu, Beichen Zhang, Runji Lin, Bowen Yu, Dayiheng Liu, Jingren Zhou, and Junyang Lin. The lessons of developing process reward models in mathematical reasoning. arXiv:2501.07301, 2025. URL https://arxiv.org/abs/2501.07301.
- Jiangjiang Zhao, Zhuoran Wang, and Fangchun Yang. Genetic prompt search via exploiting language model probabilities. In Edith Elkind (ed.), Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, pp. 5296–5305. International Joint Conferences on Artificial Intelligence Organization, 8 2023. doi: 10.24963/ijcai.2023/588. URL https://doi.org/10.24963/ijcai.2023/588. Main Track.
- Han Zhong, Zikang Shan, Guhao Feng, Wei Xiong, Xinle Cheng, Li Zhao, Di He, Jiang Bian, and Liwei Wang. DPO meets PPO: Reinforced token optimization for RLHF. In Forty-second International Conference on Machine Learning, 2025. URL https://openreview.net/ forum?id=IfWKVF6LfY.
A APPENDIX
A.1 EXPERIMENTAL SETUP
Experimental setup for the Countdown experiments. Representative models from the Qwen2.5 family (0.5B–7B) and the LLaMA3 family (1B–8B) were fine-tuned for this task. For the PPO experiments, a grid search was first performed around common hyperparameter settings and the best-performing values used (Table 3). For the GRPO experiments, a grid search was performed around the settings of Pan et al. (2025) and the best-performing values used. GRPO experiments were run with two different group sizes: N=8, following the common practice in GRPO training for the Countdown task, and N=30, aligning with the population size in ES. For all the ES, GRPO and PPO, the total number of sample evaluations was the same. The ES population size was N=30, noise scale $\sigma=0.001$ , and learning rate $\alpha=5\times10^{-4}$ across all experiments. To evaluate accuracy, a set of 200 samples were used during training, and a different set of 2000 samples during testing. For ES, results were reported on the test set after training for 500 iterations. For RL, the training was stopped after the same total number of sample evaluations as in the ES runs. An example of the prompt and the response is provided in Appendix A.2.
| Method | Model | (1e-3, 1e-6) | (1e-3, 1e-5) | (5e-3, 1e-6) | (5e-3, 1e-5) |
|---|---|---|---|---|---|
| Qwen-0.5B-Instruct | ✓ | ||||
| Qwen-1.5B-Instruct | $\checkmark$ | ||||
| Qwen-3B-Instruct | $\checkmark$ | ||||
| PPO | Qwen-7B-Instruct | $\checkmark$ | |||
| LLaMA-1B-Instruct | $\checkmark$ | ||||
| LLaMA-3B-Instruct | $\checkmark$ | ||||
| LLaMA-8B-Instruct | ✓ | ||||
| GRPO | Qwen-0.5B-Instruct | ✓ | |||
| Qwen-1.5B-Instruct | $\checkmark$ | ||||
| Qwen-3B-Instruct | $\checkmark$ | ||||
| Qwen-7B-Instruct | $\checkmark$ | ||||
| LLaMA-1B-Instruct | $\checkmark$ | ||||
| LLaMA-3B-Instruct | $\checkmark$ | ||||
| LLaMA-8B-Instruct | $\checkmark$ |
Table 3: Hyperparameter Sweep across Models under PPO and GRPO. Each pair $(\cdot, \cdot)$ denotes (KL-divergence penalty coefficient $\beta$ , learning rate $\alpha$ ); the label ' $\checkmark$ ' indicates the best hyperparameter setting for each model-method combination.
Experimental setup for the Conciseness experiments. In each experiment, Qwen-2.5-7B-Instruct (Yang et al., 2025) was fine-tuned using both ES and GRPO and evaluated using a held-out evaluation set. Each run was repeated four times, using a different random seed each time. For each GRPO experiment, the group size N=30, and learning rate $\alpha=5\times10^{-6}$ . Ten log-spaced values from 0.01 to 1.0 were evaluated for the the KL-divergence penalty coefficient $\beta$ , as well as $\beta=0.0$ . Appendix A.3 presents additional experiments with varying $\alpha$ and $\beta$ values. For ES, the population size N=30, ensuring that GRPO and ES generated the same number of responses per prompt, resulting in the same training exposure. Models were fine-tuned with $\sigma=\{0.0005,0.001,0.0015\}$ , with a learning rate $\alpha=\frac{\sigma}{2}$ . Both GRPO and ES experiments were run for 1,000 iterations, and a checkpoint saved every 200 iterations. Table 4 shows the dataset of prompts and verifiable solutions used during fine-tuning; note that it consists of only two examples. Similarly, Table 5 lists the prompts and verifiable solutions used in evaluating each fine-tuned model.
A.2 Examples of Countdown Task Outputs
Figure A.2 shows an example of the Qwen2.5-3B model's output on the Countdown task after 400 ES iterations. In order to improve accuracy, the model learned to adjust its formulas by comparing the generated answer with the correct one, and to verify its own answers for correctness.
| Prompt | Verifiable Solution | |
|---|---|---|
| Solve: $3 + 5 =$ | 8 | |
| If all birds can fly and penguins are birds, can penguins fly | No |
Table 4: Prompts and verifiable solutions used in fine-tuning the models for conciseness. Two examples is enough to achieve this goal.
| Prompt | Verifiable Solution |
|---|---|
| What is the capital of France? | Paris |
| Calculate: $12 \times 7 =$ | 84 |
| Is the statement "All cats are mammals" true or false? | True |
| What comes next in the sequence: $2, 4, 6, 8, ?$ | 10 |
| Translate "Hello" to Spanish: | Hola |
| What is 15% of 200? | 30 |
| Name one primary color: | Red |
| How many days are in a week? | 7 |
Table 5: Prompts and verifiable solutions used to evaluate the fine-tuned models. More examples are necessary than during fine-tuning to make the evaluation reliable.
Iteration 400
[1] Input:
You are a helpful assistant. You first think about the reasoning process in your mind and then provide the user with the answer. Using the numbers [28 3 4 52], create an equation that equals 44. You can use basic arithmetic operations (+, -, *, /) and each number can only be used once. Show your work in
[1] Response:
-
- Start with simple addition and subtraction: -49 + 41 73 = 80 73 = 7 (too high) -49 41 + 73 = 8 + 73 = 81 (too high) -73 49 41 = 24 41 = -17 (too low)
-
- Try multiplication and division: $(49 * 41) / 73 = 2029 / 73 \approx 27.83$ (not close to 17) $(73 * 41) / 49 = 3013 / 49 \approx 61.47$ (too high) $(49 * 73) / 41 = 3637 / 41 \approx 88.80$ (too high) $(41 * 73) / 49 = 3013 / 49 \approx 61.47$ (same as above)
-
- Check different orders: -73 (49 + 41) = 73 90 = -17 (too low) -49 (73 41) = 49 32 = 17 (this looks promising)
So, the equation 49 - (73 - 41) equals 17. Let's verify it: - Calculate inside the parentheses first: 73 - 41 = 32 - Then subtract from $49 \cdot 49 - 32 = 17$
This satisfies our requirement.
Reward: 1.1000 (Format: 1.0000, Answer: 1.0000)
Figure 2: An example of a countdown task interaction.
A.3 EXTENDED CONCISENESS EXPERIMENTS
In this section, the conciseness experiments are extended to investigate the impact of different learning rates on GRPO training.
GRPO with different learning rates. Further GRPO experiments were run over four seeds with $\beta = \{0, 0.01, 0.1, 1.0\}$ , varying the learning rate $\alpha = \{2 \times 10^{-6}, 3 \times 10^{-6}, 4 \times 10^{-6}, 5 \times 10^{-6}\}$ . A total of 20 responses were sampled per evaluation prompt. Figure 3a shows the mean reward and KL
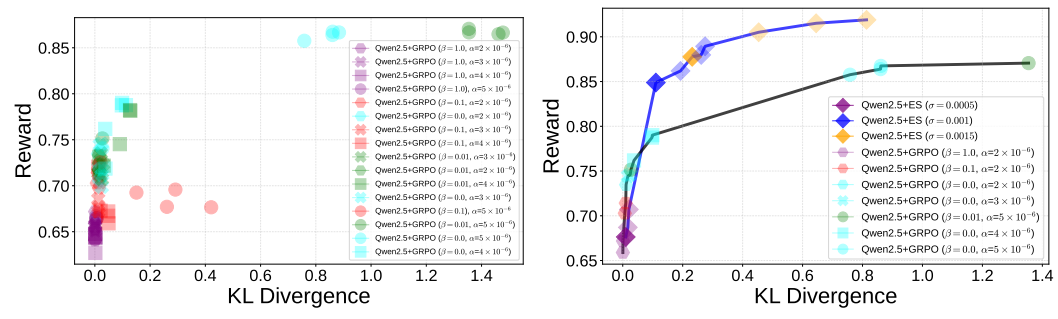
- (a) GRPO models results over various learning rates.
- (b) ES and GRPO Pareto fronts.
Figure 3: GRPO behavior with different learning rates. (a) GRPO models trained using different learning rates and $\beta$ values. Both conciseness reward and KL divergence increase with higher learning rates. (b) The ES Pareto front (blue line, top) plotted with the GRPO Pareto front (black line, bottom) over different model learning parameters. ES dominates GRPO across the whole range.
divergence of each fine-tuned model. As the learning rate increases, both mean reward and mean KL divergence increase. The best models with respect to reward are trained using $5\times 10^{-6}$ and $\beta=\{0.0,0.01\}$ , obtaining rewards greater than 0.85. Figure 3b further displays the GRPO Pareto front (black line, bottom) across these learning rates, comparing it with the ES Pareto front (blue line, top). The majority of Pareto optimal models across these learning rates obtain a mean reward of less than 0.8 and a KL divergence of less than 0.4. The ES Pareto front dominates that of GRPO over different learning rates and $\beta$ values.
Next, the reward distribution for each $\alpha$ and $\beta$ value for GRPO was compared with that of ES, starting with learning rates $2\times 10^{-6}$ and $3\times 10^{-6}$ . Figures 4a and Figure 4b show that all GRPO models stay close to the Qwen2.5-7B-Instruct base model reward distribution, despite the variation in $\beta$ . In contrast, ES shifts the reward distribution to the right with a density peak around 1.0, i.e. towards higher rewards. The learning rate was then further increased to $4\times 10^{-6}$ (Figure 4c). As a result, for $\beta=0.0$ and $\beta=0.01$ , GRPO shifts the reward distribution to the right towards higher rewards. However, they are still lower than those of ES. As the learning rate is increased further to $5\times 10^{-6}$ (Figure 4d), GRPO is sufficiently able to optimize the reward: with $\beta=0.0$ and $\beta=0.01$ , it peaks around 1.0. Thus, high learning rate combined with low $\beta$ is important for GRPO to optimize the reward. However, as was discussed before, such a setting often breaks the performance of the model.
A.4 TRAINING CURVES AND ACCURACY IMPROVEMENT OF ES AND RL ON THE COUNTDOWN TASK
As shown in Figure 6, ES consistently outperformed RL across all tested models throughout training. On smaller models such as Qwen2.5-0.5B and Llama-3.2-1B, RL showed almost no improvement, whereas ES steadily increased accuracy. On mid-sized models like Qwen2.5-1.5B, Qwen2.5-3B and Llama-3.2-3B, ES achieved substantial gains, reaching accuracy levels that RL never approached even in extended training. On larger models such as Qwen2.5-7B and Llama-3.1-8B, RL improved more than in the smaller models, but ES still maintained a clear and consistent advantage, achieving the highest accuracy throughout. In addition, as shown in Figure 5, we compute the relative improvements of PPO, GRPO, and ES over their respective base models across different model families. ES delivers the consistently largest improvements in all cases.
A.5 PARAMETER MAGNITUDE SHIFTS BY EVOLUTIONARY FINE-TUNING
This section characterizes how parameter magnitudes changed in ES fine-tuning in the countdown and conciseness experiments. Specifically, Figures 7 and 8, left column, show histograms of the absolute parameter magnitude shifts $\Delta$ before and after finetuning Llama and Qwen models, overlaid with random walk, on the Countdown task reported in Table 1. The right column in these figures shows the difference between $\Delta$ and the random walk.
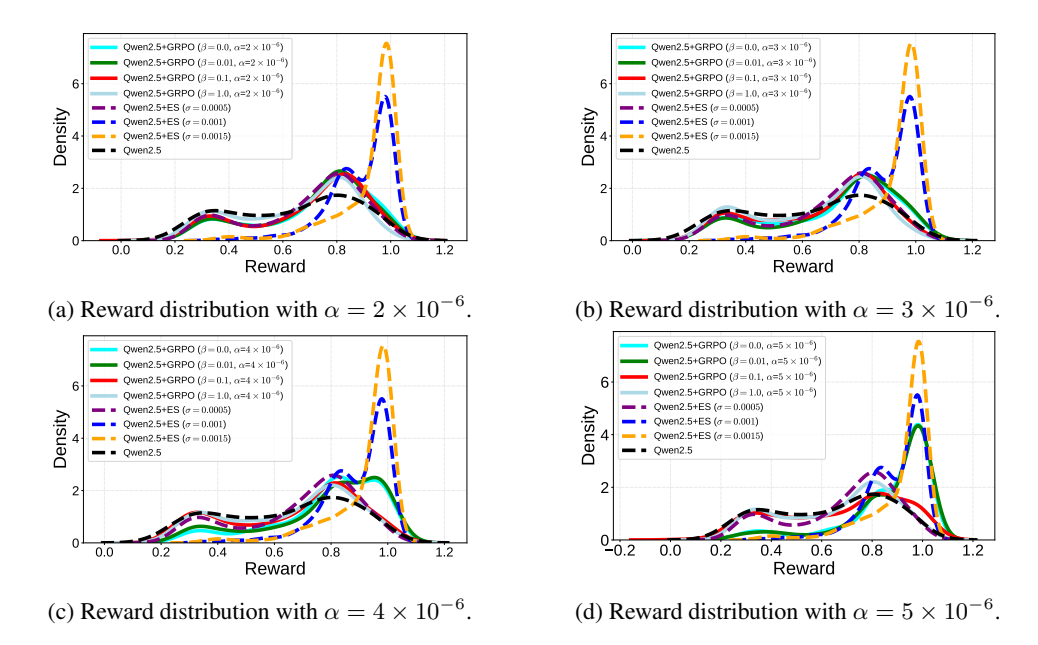
Figure 4: Reward distributions in fine-tuning for conciseness with different learning rates $\alpha = \{2 \times 10^{-6}, 3 \times 10^{-6}, 4 \times 10^{-6}, 5 \times 10^{-6}\}$ and $\beta = \{0.0, 0.01, 0.1, 1.0\}$ compared to ES on the Qwen2.5-7B-Instruct base model. Whereas GRPO distribution is similar to the base model, ES shifts it to the right, i.e. higher rewards. Higher rewards can only be achieved with GRPO with high learning rates and low $\beta$ , which setting often breaks to model's performance.
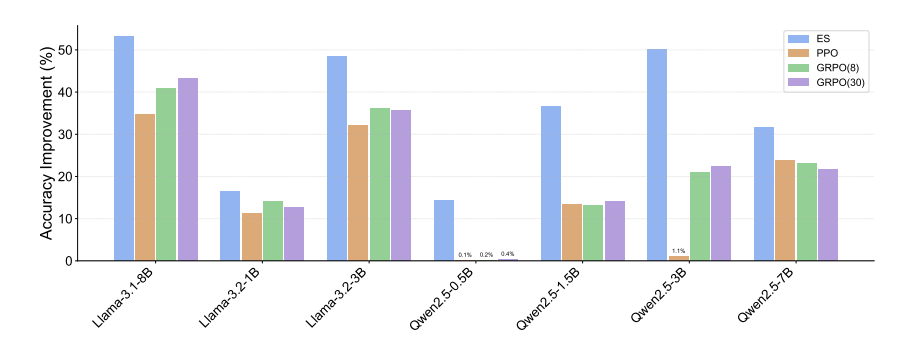
Figure 5: Accuracy Improvement over Base Models with ES vs RL across Model Families. ES results in consistently largest improvements in all cases.
For most models, $\Delta$ deviates very little from random walk. This is a counterintuitive result since fine-tuning actually resulted in a significant performance boost. A closer inspection reveals that most of the deviation was concentrated around zero. A likely explanation is that there are precision issues around zero, particularly with small bin sizes, which may lead to such deviations.
More significantly, a systematic deviation from the random walk was observed in conciseness fine-tuning of the largest model, Qwen2.5-7B-Instruct (Figure 9). The distribution shifts toward abundant small magnitude edits, suggesting that small parameter tweaks may be most significant in influencing output behavior. This result reinforces observations in prior studies (e.g. Liu et al., 2025). A possible explanation is that large models encode functionality in a more redundandant manner, and therefore minor tweaks are sufficient to achieve fine-tuning objectives. In fact, the changes are nearly indistinguishable from random walk in Figures 7 and 8 likely because they are benevolent wrt. the fine-tuning objective. A more thorough investigation of these hypotheses is a most interesting direction of future work, potentially resulting in a better understanding of fine-tuning and information processing principles in LLMs in general.
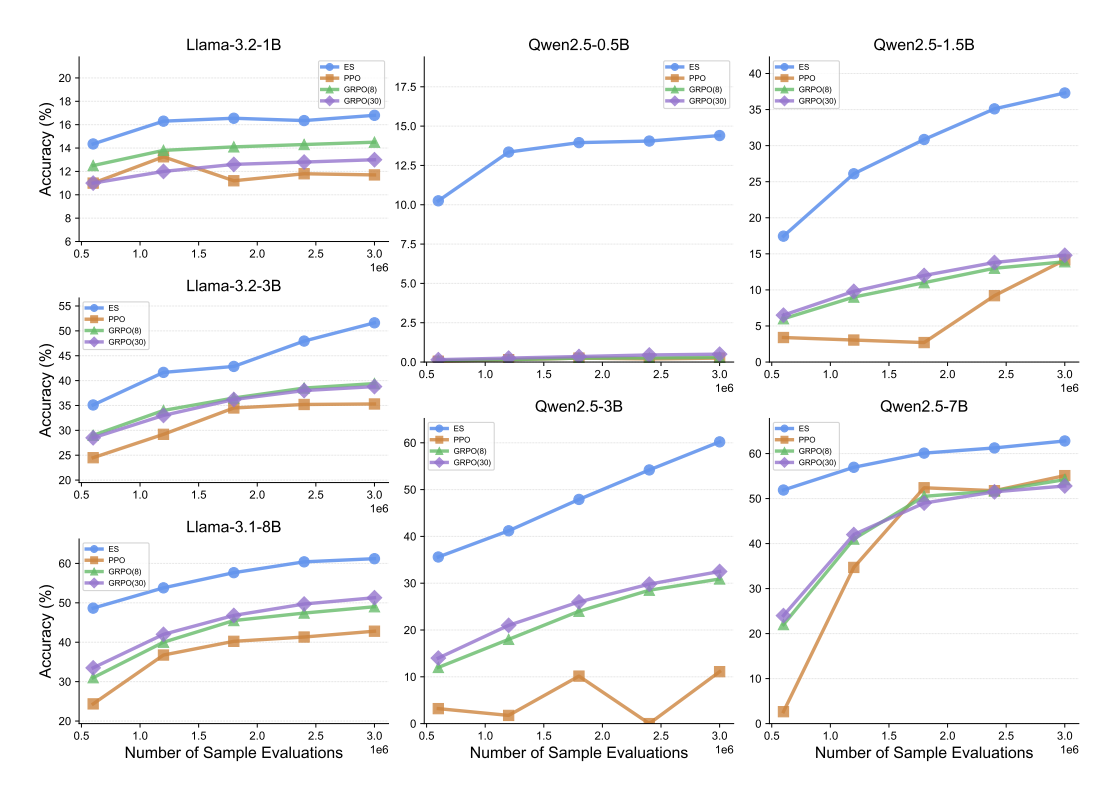
Figure 6: Training curves of ES and RL across two model families and six sizes in the countdown task. ES fine-tuning results in significantly better performance in all cases. It is able to improve even the smallest model where RL methods are ineffective. ES is also more sample efficient than RL: in most cases, it only needs less than 20% of the training sample evaluations of RL to achieve similar performance.
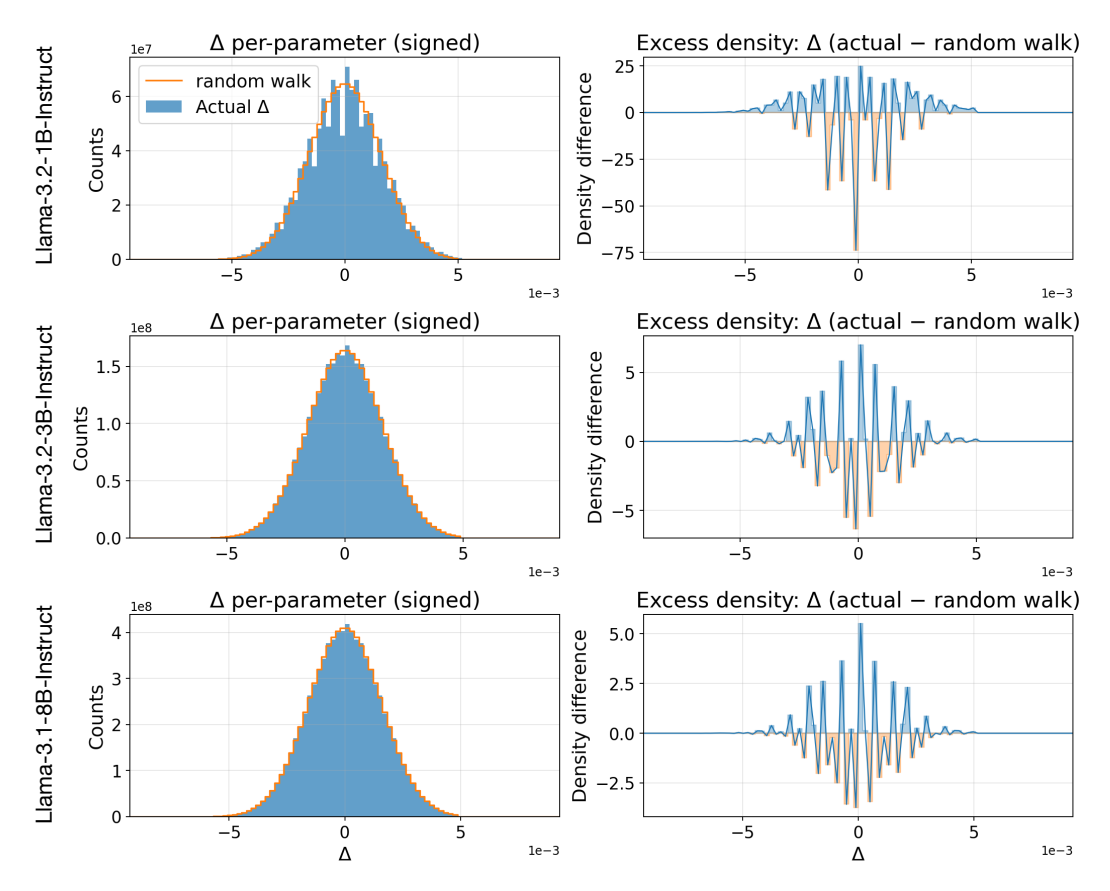
Figure 7: Parameter magnitude shift histograms for the Countdown task in Llama models optimized by ES. The changes are similar to those of a random walk, concentrated around zero, likely due to numerical inaccuracies.
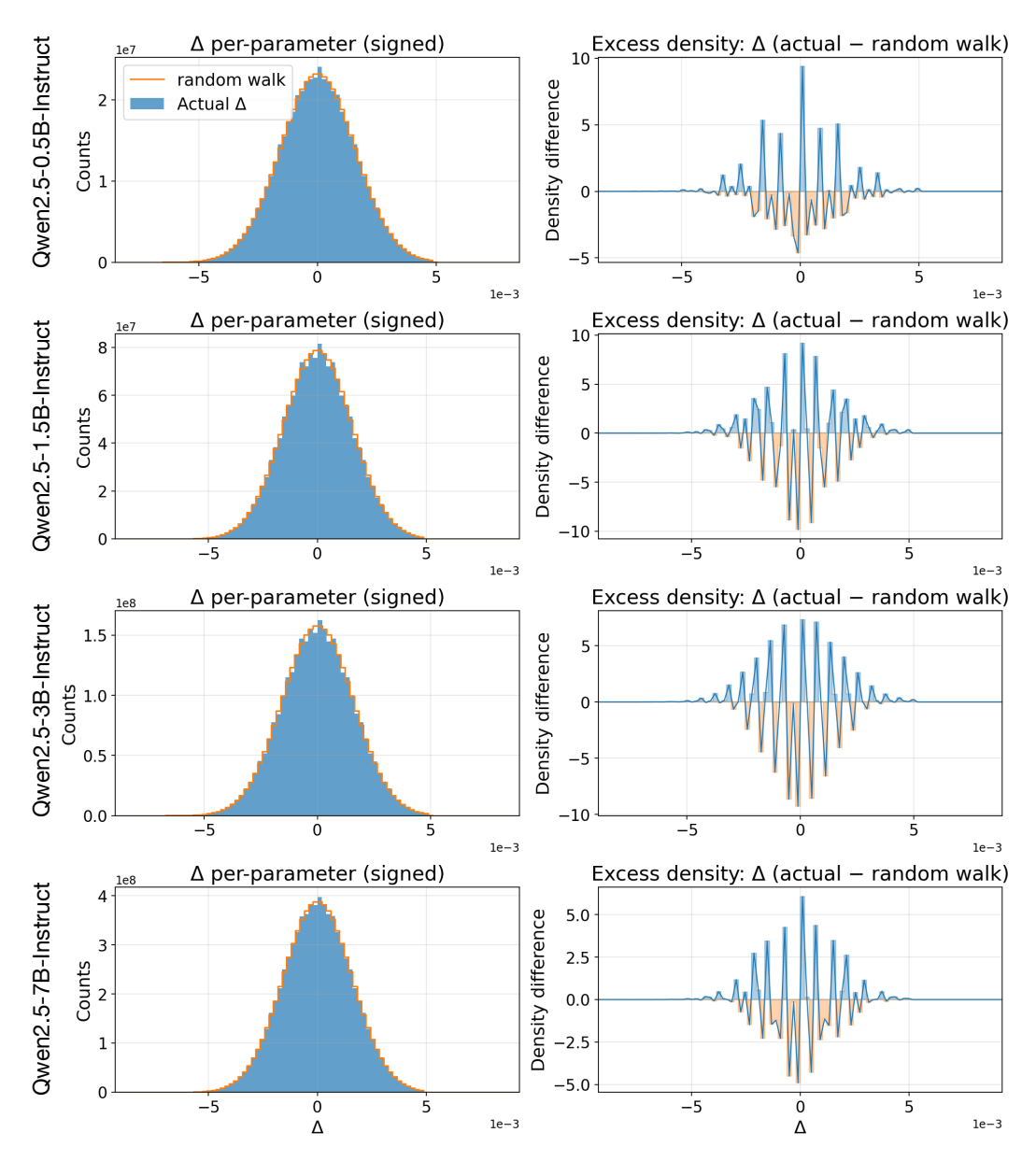
Figure 8: Parameter magnitude shift histograms for the Countdown task in Qwen models optimized by ES. The results are consistent with those observed in Llama models.
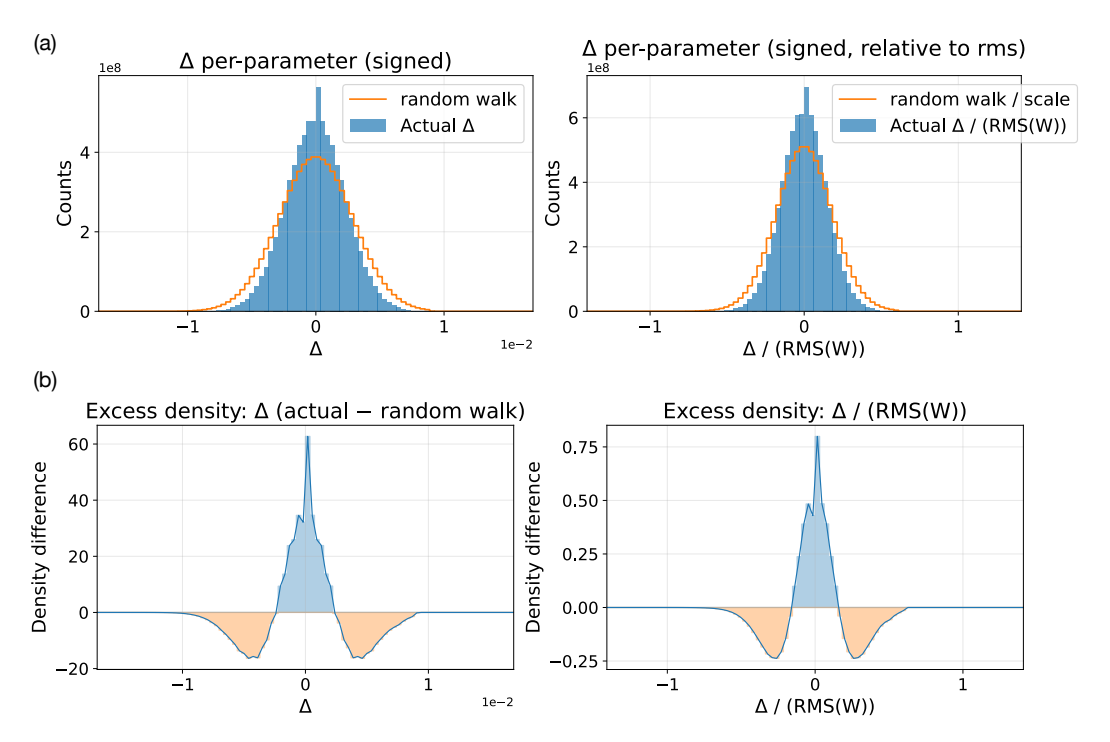
Figure 9: Parameter magnitude shift histograms in conciseness fine-tuning in Qwen2.5-7B-Instruct model with ES. In this case, the model is large and the fine-tuning goals is different, revealing a potentially significant pattern of primarily small changes. The hypothesis (to be analyzed more thoroughly in future work) is that behavior is coded in large models in a redundant manner, making it possible to achieve this fine-tuning objective through numerous small changes.