title: Neural Cellular Automata: From Cells to Pixels url: http://arxiv.org/abs/2506.22899v1

Neural Cellular Automata: From Cells to Pixels

Ehsan Pajouheshgar^{1} , Yitao Xu^{1} , Ali Abbasi^{2}† , Alexander Mordvintsev^{3} , Wenzel Jakob^{1} , Sabine Susstrunk ¨ 1 ¹School of Computer and Communication Sciences, EPFL, Switzerland ²Sharif University of Technology, Iran; ³Google Research, Zurich, Switzerland †Work done during internship at EPFL

Figure 1: Summary of result. Our proposed method enables NCA to generate high-quality outputs with minimal extra cost. Our method is applicable to different NCA architectures and different training targets. Left: Growing 2D shapes and images from a single seed; Middle: Texture synthesis in 2D; Right: Texture synthesis on 3D Meshes. Results are available at https: //cells2pixels.github.io.

Abstract

Neural Cellular Automata (NCAs) are bio-inspired systems in which identical cells self-organize to form complex and coherent patterns by repeatedly applying simple local rules. NCAs display striking emergent behaviors including selfregeneration, generalization and robustness to unseen situations, and spontaneous motion. Despite their success in texture synthesis and morphogenesis, NCAs remain largely confined to low-resolution grids (typically 128 × 128 or smaller). This limitation stems from (1) training time and memory requirements that grow quadratically with grid size, (2) the strictly local propagation of information which impedes longrange cell communication, and (3) the heavy compute demands of real-time inference at high resolution. In this work, we overcome this limitation by pairing NCA with a tiny, shared implicit decoder, inspired by recent advances in implicit neural representations. Following NCA evolution on a coarse grid, a lightweight decoder renders output images at arbitrary resolution. We also propose novel loss functions for both morphogenesis and texture-synthesis tasks, specifically tailored for high-resolution output with minimal memory and computation overhead. Combining our proposed architecture and loss functions brings substantial improvement in quality, efficiency, and performance. NCAs equipped with our implicit decoder can generate full-HD outputs in real time while preserving their self-organizing, emergent properties. Moreover, because each MLP processes cell states independently, inference remains highly parallelizable and efficient. We demonstrate the applicability of our approach across multiple NCA variants (on 2D, 3D grids, and 3D meshes) and multiple tasks, including texture generation and morphogenesis (growing patterns from a seed), showing that with our proposed framework, NCAs seamlessly scale to high-resolution outputs with minimal computational overhead.

Introduction

Complex self-organizing systems consist of numerous simple components that interact through simple1 local2 rules, producing coherent macro behavior without centralized control. In nature, such systems manifest across many scales: elementary particles bind into atoms and molecules, which then assemble into the diverse materials we observe; A single fertilized cell undergoes differentiation to form a fully developed organism during morphogenesis; and neurons coordinate and synchronize their activations to support coherent cognitive functions. In all cases, the global structure emerges not from top-down planning but from the collective effect of countless simple local interactions.

Early computational explorations of self-organization trace back to Alan Turing's reaction-diffusion model of morphogenesis [28] and John von Neumann's formulation of cellular automata [12]. Both lines of work revealed that simple hand-crafted local rules, applied through time, can yield intricate global patterns, and they opened a rigorous computational pathway for studying complex systems in biology, physics, and computer science. Neural Cellular Automata (NCAs) marked a turning point, addressing a key limitation of earlier hand-designed rules by integrating neural networks into self-organizing systems and enabling data-driven discovery of local rules [10]. Once trained, an NCA can grow complex shapes or images from a single seed [10, 25] or create rich patterns and textures [13, 15, 16, 17]. Because it learns an underlying self-organizing process rather than a direct mapping, the model inherits many distinctive features of natural self-organizing systems: robustness to perturbations and the ability to heal damaged regions [10], generalization to unseen environments such as different grid resolutions or mesh topologies [16], and emergent life-like spontaneous motion [31], all while encoding the entire process with a lightweight, compute-efficient neural network.

In practice, current NCAs are trained on relatively lowresolution grids [10, 15, 17], volumes [30], or meshes [16] containing roughly 10⁴ ∼ 10⁵ cells, which translates to spatial resolutions of about 64 × 64 to 256 × 256 depending

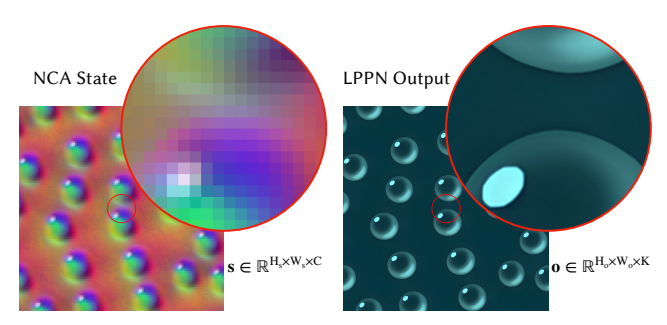
Figure 2: Sample Output of Our Hybrid Model. The NCA evolves on a coarse 128 × 128 lattice while our Local Pattern Producing Network (LPPN) renders an RGB image at 1024 × 1024 and, without retraining, at 8192 × 8192 in the magnified inset.

on the space dimensionality. This limitation arises from a combination of multiple practical and architectural constraints. First, training time and memory scale quadratically with cell grid size, quickly exhausting computational resources. Second, naive attempts to scale the grid quickly run into a communication bottleneck. Information propagates only one cell per update, so larger grids require many more steps for distant cells to communicate, which hinders model training and convergence. Third, although one could try to accelerate communication with larger convolution kernels or global operations, such fixes either run too slowly on edge devices or undermine the locality that gives NCAs their unique self-organizing properties. Consequently, it remains unclear whether NCAs can produce high-quality, high-resolution outputs while retaining their computational efficiency and characteristic emergent properties.

To overcome these limitations, and drawing on recent advances in implicit neural representations (INRs) [24, 9, 11], we pair NCA with a lightweight coordinate-based decoder, thereby decoupling NCA lattice size from output resolution. INRs were initially conceived as an approach to abstract away both time and locality in modeling embryonic pattern formation, generating an entire structure with a single neural network whose hidden layers correspond to successive developmental stages [24]. By combining NCAs and INRs, we adopt a hybrid approach: The NCA maintains an explicit, modest-sized grid of cells that evolve through local interactions, gradually producing a coarse feature map3 . An Local Pattern Producing Network (LPPN), shared by all cells, then takes a locally averaged cell state together with continuous localized coordinates and produces the output color at any arbitrary position between the cells. From the biology perspective, the NCA provides the high-level blueprint that determines where structure should emerge, while the LPPN sidesteps the intricate biochemical refinement pro-

¹By simple rules, we mean interaction mechanisms with low descriptional complexity relative to the complexity of the resulting emergent behavior.

²While locality of interactions is not strictly required in a complex system, every self-organizing system observed in nature relies on local interactions among its components.

³Biologically analogous to early gene-expression gradients which provide positional cues for subsequent formations of tissues and organs.

cesses and instead renders those details in a single pass. This division of labor preserves the NCA's locality and emergent self-organizing properties, while enabling the model to scale seamlessly from coarse cell grids to fine-grained, highresolution outputs, as shown in Figure 2.

We train the NCA and LPPN jointly, end to end. The recurrent NCA, with only a few thousand trainable weights, still evolves on its coarse grid while the lightweight LPPN (adding roughly 20 ∼ 30% more parameters) is invoked only to render high-resolution outputs for the loss evaluation. Because all recurrent updates happen at low resolution, training remains memory-efficient and fast, yet the added LPPN greatly increases the model's capacity. The LPPN is a tiny Multi-Layered Perceptron (MLP) applied independently to every cell. Thus, inference remains fully parallelizable on modern GPUs and fast even on edge devices. We apply our method to the two most common NCA tasks: growing shapes or images from a seed [10, 25] and texture synthesis [13, 15, 16, 17, 30]. To supervise these tasks at high resolution, we propose tailored loss functions that add only minimal memory or computation overhead. We demonstrate that our hybrid framework adapts effortlessly to NCAs operating on diverse spatial domains, from 2D grids [10, 13, 15, 17] to 3D voxel grids [8, 25, 30] and 3D meshes [16]. Across all these settings, our model retains the characteristic self-organizing properties of NCAs, along with their efficiency and interactive controllability.

Related Works

Neural Cellular Automata

The seminal studies of Alan Turing on reaction–diffusion systems [28] and John von Neumann on cellular-automaton [12] laid the foundation for computational models of selforganization. In general, these systems consist of a set of cells living on a grid. Three main components, cell state, neighborhood, and update rule, fully characterize one such system. Cells interact with their neighbors and repeatedly adapt to the environment by updating their cell states according to the rule. Carefully hand-designed CA and reaction–diffusion rules have reproduced 2D and 3D morphogenesis and texture phenomena [2, 4, 29], yet the need for laborious manual rule search has long limited further exploration.

Renewed attention to cellular automata began with Gilpin [3], which showed that a classical CA update can be written as a shallow convolutional neural network and therefore trained with back-propagation. Extending this idea, Mordvintsev et al. [10] parameterize the update rule by an MLP, and use fixed convolutional kernels for cell interaction modeling, giving rise to Neural Cellular Automata. This MLP parameterization allows NCA to learn directly from data. NCA's data-driven formulation sparked a surge of interest, and researchers have since achieved impressive results in a range of tasks and domains by combining NCAs with modern deep-learning techniques.

Morphogenesis Mordvintsev et al. [10] proposed the first NCA model for 2D morphogenesis, demonstrating that a single, shared update rule with only a few thousand parameters can grow an image from a one-pixel seed with the ability to regenerate. Sudhakaran et al. [25] extended the model to three dimensions by using 3-D convolutions, enabling NCAs to construct large Minecraft structures and simple functional machines that can self-repair when blocks are removed. Sudhakaran et al. [26] augments each cell state with a condition vector, allowing the same NCA to switch behaviors on the fly and grow multiple target shapes.

Texture Synthesis Niklasson et al. [13] first applied NCAs to texture synthesis, showing that a lightweight NCA can synthesize a target exemplar texture while exhibiting subtle spontaneous motion, underscoring the intrinsically dynamic nature of the model. Building on this idea, Pajouheshgar et al. [15] introduced a training scheme that supervises both appearance and motion towards user-specified targets, enabling real-time controllable synthesis of dynamic textures. To improve stability under finer spatial and temporal sampling, Pajouheshgar et al. [17] showed that, when seeded with noise, NCAs learn a true underlying partial differential equation (PDE), enabling continuous scale control and multi-resolution synthesis. Finally, Pajouheshgar et al. [16] extended NCA from planar grids to arbitrary meshes by replacing 2D convolutions with non-parametric sphericalharmonic-based message passing, allowing NCAs to synthesize textures directly on 3D meshes.

Generative Modeling Palm et al. [18] cast NCAs into a variational framework for diverse image synthesis. Otte et al. [14] combines NCAs with adversarial training to improve out-of-distribution generalization [14]. Tesfaldet et al. [27] augment NCAs with spatially localized self-attention, creating Vision Transformer Cellular Automata (ViTCA) that achieve strong denoising and representation-learning performance while avoiding the full quadratic cost of global attention. Finally [7] propose an NCA-based denoising diffusion model that can images with far fewer parameters than UNet backbones.

Discriminative Tasks Randazzo et al. [20] design an NCA whose pixels communicate locally on an MNIST digit and gradually self-organize their states until the grid reaches a global consensus, yielding a one-hot label map. Xu et al. [32] inserts small NCAs between ViT layers to improve adversarial robustness and out of distribution generalization of transformers. Sandler et al. [22] achieves efficient image segmentation with an NCA model with less than 10k parameters [21]. Kalkhof et al. [6] segments medical scans on a Raspberry Pi while being significantly smaller than the U-Net baseline. Guichard et al. [5] applies developmental NCA dynamics to solve tasks in the ARC reasoning benchmark [1].

Despite significant progress, almost all existing NCAs still operate on grids or meshes with no more than a few hundred thousand cells, which limits their ability to produce high-resolution outputs. Scaling further is impeded by GPU memory limits, slow information propagation in large grids, and the locality-breaking global operations often introduced as work-arounds. Our approach removes this resolution barrier by pairing an NCA that runs on a coarse grid with a lightweight implicit decoder that renders fine detail at arbitrary resolution. The result preserves the NCA's characteristic self-organizing properties and real-time efficiency, while delivering high-quality outputs at resolutions previously out of reach.

Implicit Neural Representation

Compositional Pattern Producing Networks (CPPNs) introduced the idea of Implicit Neural Representation (INR) by modeling an entire image as a continuous coordinatebased function fθ(x, y) implemented by a compact feedforward network, whose hidden layers loosely mirror successive developmental stages [24]. By composing periodic or radial activation functions, CPPNs can generate arbitrarily high-resolution patterns without simulating local interactions over time. CPPN weights and connections were originally tuned using evolutionary strategies.

Recently, INRs have gained significant popularity in computer vision and graphics, where coordinate-based neural networks are trained with gradient descent instead of evolutionary search. Park et al. [19] apply a coordinate-based MLP to 3-D geometry to learn a continuous signed-distance function (SDF) conditioned on a latent code, producing compact, watertight shapes. Building on this, Mildenhall et al. [9] propose Neural Radiance Field (NeRF), a 5-D neural radiance field that maps a 3-D position and viewing direction to color and density. NeRF uses a sinusoidal positional encoding of the input coordinates to mitigate the spectral bias of MLP networks with ReLU activation, enabling high-fidelity novel-view synthesis. Finally, Sitzmann et al. [23] show that replacing standard MLP activations with sinusoidal functions lets a modest-sized network capture highfrequency details across 1-D, 2-D and 3-D signals while improving convergence speed and eliminating the need for manual positional encoding.

While these models produce continuous, resolution-free signals, they can be slow to train and difficult to interpret or edit because semantic structure is buried in dense weights. Muller et al. [ ¨ 11] mitigates the speed issue by combining a multi-resolution hash-grid encoding with a small MLP, cutting NeRF training from hours to minutes. Our hybrid approach is conceptually similar: we also supply the decoder with a rich embedding, but instead of learning a hash grid we let an NCA evolve a low-resolution lattice whose cell states act as the embedding. This lattice is explicit, interpretable, and local, enabling user interaction, while the lightweight decoder supplies the high-frequency detail.

Neural Cellular Automata

A Neural Cellular Automata (NCA) models the cell evolution on a grid over time. Let si,t ∈ R ^C denote the Cdimensional vector storing the i-th cell state at time t. At each time step, cells perceive their neighbors in the Perception stage Z, to collect the information of their surrounding environment. According to such information, cells adapt to the environment by updating the states in the Adaptation stage A. The perception Z is often instantiated using convolution for 2D and 3D grids [10, 13, 15, 17, 25], or a convolution-like operator for meshes [16]. The adaptation function A is commonly parametrized by a Multi Layered Perceptron (MLP), which sometimes includes a stochastic term [10, 13, 15, 16, 32]. The state of cell i, s^{i} , is updated following Eq. 1.

$$\mathbf{s}_{i}^{t+\Delta t} = \mathbf{s}_{i}^{t} + \mathcal{A}(\mathcal{Z}(\mathbf{s}_{i}^{t}, \mathbf{s}_{j}^{t})) \cdot \Delta t, \quad j \in \mathcal{N}(i). \tag{1} $$

N (i) denotes the set of neighbors of cell i. After evolving for T steps, the cell states s^{T} of all cells can be extracted for further downstream applications. We forward the resulting cell states to the Local Pattern Producing Network, which transforms the low-resolution NCA features in s^{T} into highresolution detailed output.

Local Pattern Producing Network (LPPN)

The LPPN converts the coarse NCA lattice into a highresolution field by evaluating a small MLP decoder network at every sampling point p, 4 as shown in Figure 3. For each p, the decoder is supplied with:

• 1. locally averaged cell state s¯(p) ∈ R ^C , that aggregates the states of the cells in p's surrounding primitive.
• 1. local coordinate vector u(p) that encodes the relative position of p inside its primitive.

Primitives

A primitive Ω consists of the cells surrounding p along with the geometric shape determined by their positions. A primitive's shape is determined by the underlying lattice; on a 2D quad grid, for instance, the defacto primitive would be a rectangle. Figure 4 illustrates four common primitive types. For i ∈ Ω, let v^{i} denote the position of the i-th cell in the primitive. We call a set of weights λi(p) that describes the position of any arbitrary p inside the primitive with respect to the primitive's vertices a λ-coordinate if it satisfies the three following conditions:

⁴A sampling point may be the center of a rasterized pixel for 2D images or 3D meshes, or a 3D position for a NeRF-style volumetric rendering.

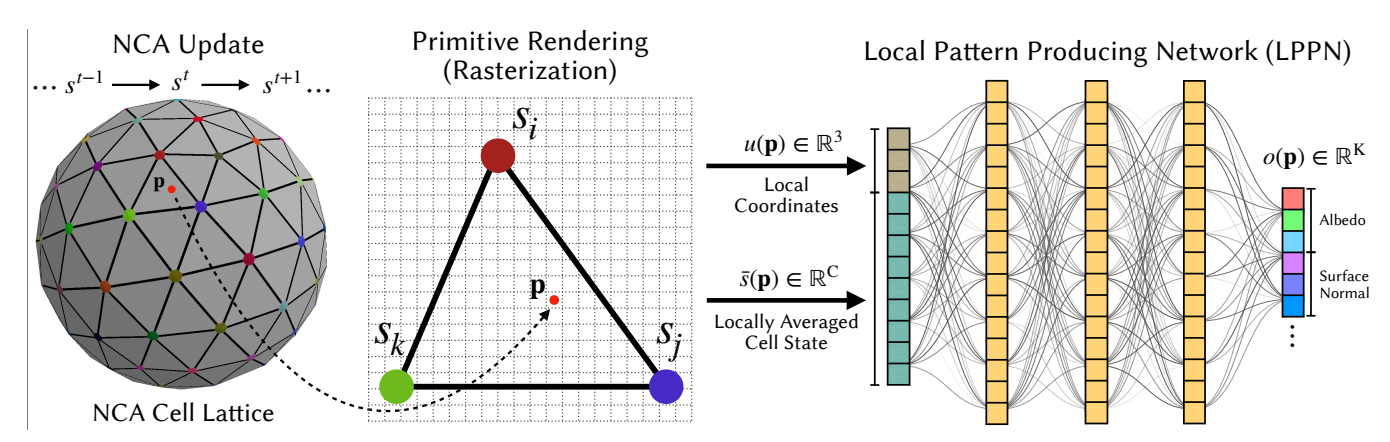
Figure 3: Hybrid NCA + LPPN Overview. Left: The NCA operates on a coarse lattice of cells (in this example vertices of a mesh) Center: A sampling point p (red dot) inside a triangle primitive, whose vertices correspond to NCA cells s^{i} , s^{j} , sk. The local coordinate u(p) expresses the point's position inside the primitive, while the locally averaged cell state s¯(p) is obtained by interpolating the surrounding cell states. Right: A shared lightweight MLP, LPPN, receives (s¯(p), u(p)) as input and outputs the appearance features, such as color and surface normal, at point p.

• 1. Partition of unity: \sum_{j \in Ω} λ^{j} (p) = 1.
• 1. Non-negativity λ^{j} (p) > 0.
• 1. Linear precision: p = \sum_{j \in Ω} λ^{j} (p)v^{j} .

While triangles admit a unique λ-coordinate (barycentric), higher-order primitives offer multiple valid choices. For the rectangular primitive, a valid choice for λcoordinates is the bilinear interpolation weights. Figure 4 illustrates the most common variants adapted in this paper for four different types of primitives. With the chosen λ–coordinate system in place, we obtain the first LPPN input by averaging the cell states within p's primitive Ω:

$$\bar{\mathbf{s}}(\mathbf{p}) = \sum_{j \in \Omega} \lambda_j(\mathbf{p}) \mathbf{s}_j \tag{2}$$

Local Coordinates

Rather than feeding the full λ-coordinates directly to the LPPN, we transform it to a more compact Local coordinate u(p), which is easier for the decoder to digest. For rectangle and cube primitives we use axis-aligned cartesian coordinates for u. This representation fully determines the point's location inside the primitive with fewer dimensions than the eight (or four) dimensional λ-coordinates. For triangular meshes and general polygonal primitives we retain the λ-coordinates. In every case we rescale each component so that u(p) ∈ [−1, 1], whereas the original λ-coordinates lie in [0, 1]. This zero-centered range removes a potential bias in the decoder's inputs and empirically improves learning. Figure 4 summarizes the specific choices of λ, u coordinates for the primitive types considered in this paper. Before passing u(p) to the LPPN, we optionally apply simple transformations that improve its continuity and uniformity, as detailed next.

Ensuring C ⁰ Continuity and Uniformity Raw ucoordinates are piecewise smooth yet generally discontinuous at primitive boundaries, as shown in middle column of Figure 5. On a 2D grid (top), the cartesian coordinates reset at each primitive, and on a triangular mesh (bottom) the barycentric coordinates change abruptly across edges. To provide the LPPN with smooth, well-conditioned positional cues, we apply simple, primitive-specific transforms to the raw u-coordinates.

For rectangle and cube primitives we keep the Cartesian coordinates but encode them with a sinusoidal basis of the first n harmonics,

$$u_{\text{aug}} = [\sin(\pi u), \cos(\pi u), \dots, \sin(n\pi u), \cos(n\pi u)].$$

which is naturally continuous at cell borders as shown in Figure 5-top-right.

For triangular or polygonal primitives the raw ucoordinates are discontinuous at primitive boundaries because neighboring faces list their vertices in arbitrary orders. To eliminate this order-dependence we first sort the ucoordinates (barycentric/mean-value) in descending order, making the most-dominant weight always the first component. This consistent reordering makes the local coordinate field C 0 across primitive boundaries, as illustrated in Figure 5,(a). Sorting, however, skews the dynamic range of the different components of u, as noted by the predominance of red in (a). We therefore pass each component through the inverse cumulative distribution function of its analytical (or empirical) distribution, spreading the values uniformly over [−1, 1]. The resulting coordinates have balanced amplitude and remain continuous across primitives (Figure 5,(b)).

However, after this sorting different components of the local coordinates have different dynamic range, as demonstrated by the dominance of the red color. To equalize the dynamic range we then map each component through the

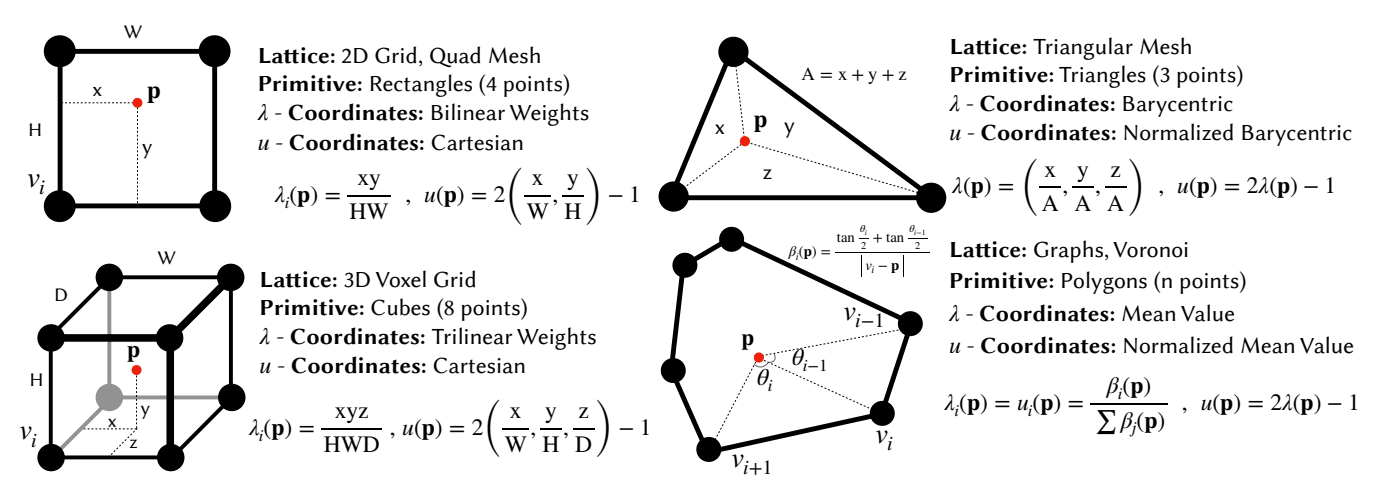
Figure 4: Representative examples of primitives. Vertices correspond to neighboring cells.

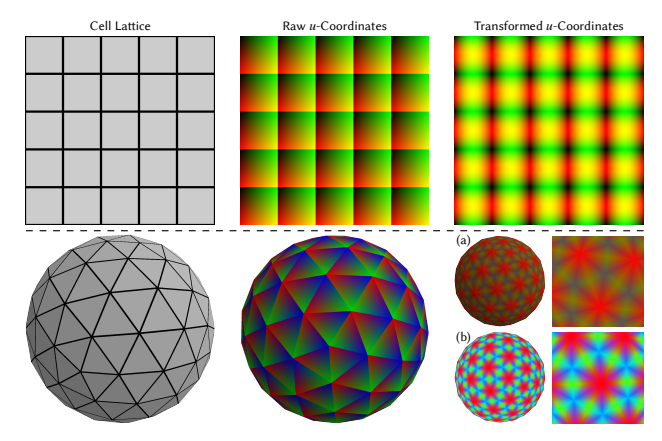
Figure 5: Local coordinate transformations. Raw u-coordinates visualized as RGB suffer discontinuities at primitive boundaries. (Top Right) Applying trigonometric functions on cartesian coordinates enforces $C^0$ continuity at boundaries for rectangle primitives. Bottom Right (a): Sorting the barycentric coordinates enforces $C^0$ continuity but yields an imbalanced dynamic range (red color dominates). (b) Applying an inverse-CDF remapping equalizes the range, giving a uniform, continuous positional field that is easier for the LPPN to digest.

inverse CDF of its empirical or analytical distribution to producing uniformly distributed continuous coordinates, as shown in Figure 5-(b).

MLP Decoder

The LPPN is a lightweight MLP $f_{\theta}$ that takes the locally averaged state and local coordinates of each sampling point $(\bar{s}(\mathbf{p}), u(\mathbf{p}))$ , and returns the desired attributes at the sampling point:

$$o(\mathbf{p}) = f_{\theta}(\bar{s}(\mathbf{p}), u(\mathbf{p})) \in \mathbb{R}^K, \tag{3} $$

where K is the number of channels in the output, e.g. K=3 for RGB-only, or K=9 when RGB is augmented with

surface normals height, ambient occlusion, and roughness maps. Because the LPPN is called only when the loss is evaluated, all recurrent NCA updates still run on the coarse lattice. Therefore adding the LPPN incurs negligible training overhead.

Loss Functions

We design tailored loss functions for different NCA tasks, including texture synthesis and morphogenesis modeling. More details will be released soon.

Experiments

We conduct experiments on 2 tasks: Morphogenesis modeling and Texture synthesis. We perform morphogenesis modeling on 2D images, as shown in the left column of Figure 1. The results of 2D and 3D texture synthesis are demonstrated in the middle and right columns of Figure 1. More details will be released soon.

Conclusion

We introduce a hybrid self-organizing framework that pairs Neural Cellular Automata with a lightweight Local Pattern Producing Network to decouples NCA grid size from output resolution. The NCA guides pattern formation through local updates on a coarse lattice, while the shared LPPN transforms a locally averaged cell state together with continuous local coordinates into appearance features at any requested scale. Our proposed task-specific loss functions designed for high resolution outputs further improves the quality without exhausting memory and compute. We demonstrate that NCA, paired with our LPPN, is capable of generating full-HD images and detailed 3D textures in real time. Our results allows NCA to scale to practical resolutions without losing their characteristic properties, such as robustness, controllability, and efficiency, paving the way for interactive, deployable self-organizing systems.

References

• [1] Francois Chollet, Mike Knoop, Gregory Kamradt, Bryan Landers, and Henry Pinkard. Arc-agi-2: A new challenge for frontier ai reasoning systems. arXiv preprint arXiv:2505.11831, 2025.
• [2] Kurt W Fleischer, David H Laidlaw, Bena L Currin, and Alan H Barr. Cellular texture generation. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques, pages 239–248, 1995.
• [3] William Gilpin. Cellular automata as convolutional neural networks. Physical Review E, 100(3):032402, 2019.
• [4] Stephane Gobron and Norishige Chiba. 3d surface cellular au- ´ tomata and their applications. The Journal of Visualization and Computer Animation, 10(3):143–158, 1999.
• [5] Etienne Guichard, Felix Reimers, Mia Kvalsund, Mikkel Lepperød, and Stefano Nichele. Arc-nca: Towards developmental solutions to the abstraction and reasoning corpus. arXiv preprint arXiv:2505.08778, 2025.
• [6] John Kalkhof, Camila Gonzalez, and Anirban Mukhopadhyay. ´ Med-NCA: Robust and lightweight segmentation with neural cellular automata. In International Conference on Information Processing in Medical Imaging, pages 705–716. Springer, 2023.
• [7] John Kalkhof, Arlene Kuhn, Yannik Frisch, and Anirban ¨ Mukhopadhyay. Frequency-time diffusion with neural cellular automata. arXiv preprint arXiv:2401.06291, 2024.
• [8] Maria Larsson, Hodaka Yamaguchi, Ehsan Pajouheshgar, I-Chao Shen, Kenji Tojo, Chia-Ming Chang, Lars Hansson, Olof Broman, Takashi Ijiri, Ariel Shamir, Wenzel Jakob, and Takeo Igarashi. The mokume dataset and inverse modeling of solid wood textures. ACM Transactions on Graphics, 44 (4):18 pages, August 2025. doi: 10.1145/3730874. URL https://doi.org/10.1145/3730874.
• [9] Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision, pages 405–421, 2020.
• [10] Alexander Mordvintsev, Ettore Randazzo, Eyvind Niklasson, and Michael Levin. Growing neural cellular automata. Distill, 2020. doi: 10.23915/distill.00023. https://distill.pub/2020/growing-ca.
• [11] Thomas Muller, Alex Evans, Christoph Schied, and Alexander ¨ Keller. Instant neural graphics primitives with a multiresolution hash encoding. ACM transactions on graphics (TOG), 41(4):1–15, 2022.
• [12] John von Neumann. Theory of self-reproducing automata. Mathematics of Computation, 21:745, 1966.
• [13] Eyvind Niklasson, Alexander Mordvintsev, Ettore Randazzo, and Michael Levin. Self-organising textures. Distill, 6(2): e00027–003, 2021.

• [14] Maximilian Otte, Quentin Delfosse, Johannes Czech, and Kristian Kersting. Generative adversarial neural cellular automata. arXiv preprint arXiv:2108.04328, 2021.

• [15] Ehsan Pajouheshgar, Yitao Xu, Tong Zhang, and Sabine Susstrunk. Dynca: Real-time dynamic texture synthesis using ¨ neural cellular automata. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 20742–20751, 2023.

• [16] Ehsan Pajouheshgar, Yitao Xu, Alexander Mordvintsev, Eyvind Niklasson, Tong Zhang, and Sabine Susstrunk. Mesh ¨ neural cellular automata. ACM Trans. Graph., 2024. doi: 10.1145/3658127. URL https://doi.org/10.1145/ 3658127.
• [17] Ehsan Pajouheshgar, Yitao Xu, and Sabine Susstrunk. ¨ Noisenca: Noisy seed improves spatio-temporal continuity of neural cellular automata. volume ALIFE 2024: Proceedings of the 2024 Artificial Life Conference of Artificial Life Conference Proceedings, page 57, 07 2024. doi: 10.1162/isal a 00785. URL https://doi.org/10.1162/isal\a\ 00785.
• [18] Rasmus Berg Palm, Miguel Gonzalez-Duque, Shyam Sud- ´ hakaran, and Sebastian Risi. Variational neural cellular automata. arXiv preprint arXiv:2201.12360, 2022.
• [19] Jeong Joon Park, Peter Florence, Julian Straub, Richard Newcombe, and Steven Lovegrove. Deepsdf: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 165–174, 2019.
• [20] Ettore Randazzo, Alexander Mordvintsev, Eyvind Niklasson, Michael Levin, and Sam Greydanus. Self-classifying mnist digits. Distill, 2020. doi: 10.23915/distill.00027.002. https://distill.pub/2020/selforg/mnist.
• [21] Mark Sandler, Andrey Zhmoginov, Liangcheng Luo, Alexander Mordvintsev, Ettore Randazzo, et al. Image segmentation via cellular automata. arXiv preprint arXiv:2008.04965, 2020.
• [22] Mark Sandler, Andrey Zhmoginov, Liangcheng Luo, Alexander Mordvintsev, Ettore Randazzo, et al. Image segmentation via cellular automata. arXiv preprint arXiv:2008.04965, 2020.
• [23] Vincent Sitzmann, Julien N.P. Martel, Alexander W. Bergman, David B. Lindell, and Gordon Wetzstein. Implicit neural representations with periodic activation functions. In Proc. NeurIPS, 2020.
• [24] Kenneth O. Stanley. Compositional pattern producing networks: A novel abstraction of development. Genetic Programming and Evolvable Machines, 8(2): 131–162, June 2007. ISSN 1389-2576. doi: 10. 1007/s10710-007-9028-8. URL https://doi.org/ 10.1007/s10710-007-9028-8.
• [25] Shyam Sudhakaran, Djordje Grbic, Siyan Li, Adam Katona, Elias Najarro, Claire Glanois, and Sebastian Risi. Growing 3d artefacts and functional machines with neural cellular automata. In 2021 Conference on Artificial Life, 2021. URL https://arxiv.org/abs/2103.08737.

• [26] Shyam Sudhakaran, Elias Najarro, and Sebastian Risi. Goalguided neural cellular automata: Learning to control selforganising systems. arXiv preprint arXiv:2205.06806, 2022.

• [27] Mattie Tesfaldet, Derek Nowrouzezahrai, and Christopher Pal. Attention-based neural cellular automata. arXiv preprint arXiv:2211.01233, 2022.

• [28] AM Turing. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London Series B, 237(641):37–72, 1952.
• [29] Greg Turk. Generating textures on arbitrary surfaces using reaction-diffusion. Acm Siggraph Computer Graphics, 25(4): 289–298, 1991.
• [30] Dongqing Wang, Ehsan Pajouheshgar, Yitao Xu, Tong Zhang, and Sabine Susstrunk. Volumetric temporal texture synthesis ¨ for smoke stylization using neural cellular automata. arXiv preprint arXiv:2502.09631, 2025.
• [31] Yitao Xu, Ehsan Pajouheshgar, and Sabine Susstrunk. Emer- ¨ gent dynamics in neural cellular automata. volume AL-IFE 2024: Proceedings of the 2024 Artificial Life Conference of Artificial Life Conference Proceedings, page 96, 07 2024. doi: 10.1162/isal a 00744. URL https://doi. org/10.1162/isal\_a\_00744.
• [32] Yitao Xu, Tong Zhang, and Sabine Susstrunk. Adanca: Neural cellular automata as adaptors for more robust vision transformer. In The Thirty-eighth Annual Conference on Neural Information Processing Systems, 2024.