Neural Cellular Automata: From Cells to Pixels

原文链接：https://arxiv.org/pdf/2506.22899

作者：Ehsan Pajouheshgar, Yitao Xu, Ali Abbasi, Alexander Mordvintsev, Wenzel Jakob, Sabine Süsstrunk

日期：2025-06

被引用：2（谷歌学术）

1. 引言

神经元胞自动机 (Neural Cellular Automata, NCA) 是一类受生物启发的自组织系统，通过重复应用简单的局部规则，使相同的细胞自组织形成复杂且连贯的模式。NCA 展现了令人惊叹的涌现行为，包括自我修复、对未见情况的泛化能力以及自发的运动。

尽管 NCA 在纹理合成和形态发生方面取得了成功，但它们长期以来被局限于低分辨率网格（通常为 $128 \times 128$ 或更小）。这种限制主要源于三个方面： 1. 计算资源限制：训练时间和内存需求随网格大小呈二次方增长。 2. 通信瓶颈：信息的严格局部传播阻碍了长距离的细胞间通信。 3. 推理开销：高分辨率下的实时推理对计算要求极高。

本文的贡献：为了克服这些限制，作者提出了一种混合架构，将 NCA 与一个微小的、共享的隐式解码器 (Implicit Decoder) 相结合。这种方法受到隐式神经表示 (Implicit Neural Representations, INR) 的启发。NCA 在粗糙的网格上进行演化，而轻量级的解码器则负责将输出图像渲染为任意分辨率。这种设计使得 NCA 能够实时生成全高清 (Full-HD) 输出，同时保留其自组织和涌现特性。

Figure 1: 结果摘要 (Summary of Result)

* 内容：展示了该方法在不同任务中的应用能力。 * Left (左)：从单个种子生长出高分辨率的 2D 形状（蜥蜴）和图像。 * Middle (中)：2D 纹理合成的高清结果。 * Right (右)：在 3D 网格 (Mesh) 上合成的高质量纹理。 * 意义：证明了该方法能够以最小的额外成本显著提升 NCA 的生成质量。

2. 方法

该论文的核心思想是：让 NCA 只在“粗网格/粗几何”上演化（负责全局结构与语义的“蓝图”），再用一个很小的坐标 MLP（LPPN）把粗网格上的细胞状态当作“低分辨率 embedding”，渲染/查询任意分辨率的连续输出场（负责高频细节）。数学上就是把

• “离散网格上的时序动力系统”（NCA 演化）
• 和“连续坐标到颜色/属性的隐式函数”（LPPN 解码）

拼在一起，并通过训练把两者端到端耦合起来。

2.0 符号与目标（先把对象说清楚）

• 细胞集合：用索引 $i\in\{1,\dots,N\}$ 表示粗网格/粗几何上的细胞（2D 网格像素、3D 体素、或 mesh 顶点）。
• 细胞状态：第 $t$ 次迭代时，第 $i$ 个细胞的状态向量 $\mathbf{s}_i^t\in\mathbb{R}^{C}$（$C$ 是通道数）。
• 采样点（输出查询点）：$\mathbf{p}$ 表示要渲染/监督的连续点（2D 图像里的像素中心，或 mesh 表面上的点等）。
• 输出：$\mathbf{o}(\mathbf{p})\in\mathbb{R}^{K}$（典型 $K=3$ 为 RGB；也可以更大，包含法线、粗糙度等）。

整体目标可以写成：学习一组参数（NCA 更新规则参数 + LPPN 参数）使得对于大量采样点 $\mathbf{p}$，预测 $\mathbf{o}(\mathbf{p})$ 逼近目标图像/纹理的真值。

2.1 混合架构

系统由两部分组成： 1. NCA (Neural Cellular Automata)：维护一个显式的、中等大小的细胞网格。细胞通过局部交互随时间演化，产生粗糙的特征图 (Feature Map)。这一步提供了结构生成的“蓝图”。 2. LPPN (Local Pattern Producing Network)：一个位置感知的、共享的轻量级 MLP（多层感知机）。它作为解码器，在渲染阶段被调用，用于生成高频细节。

混合 NCA + LPPN 概览 (Hybrid NCA + LPPN Overview)

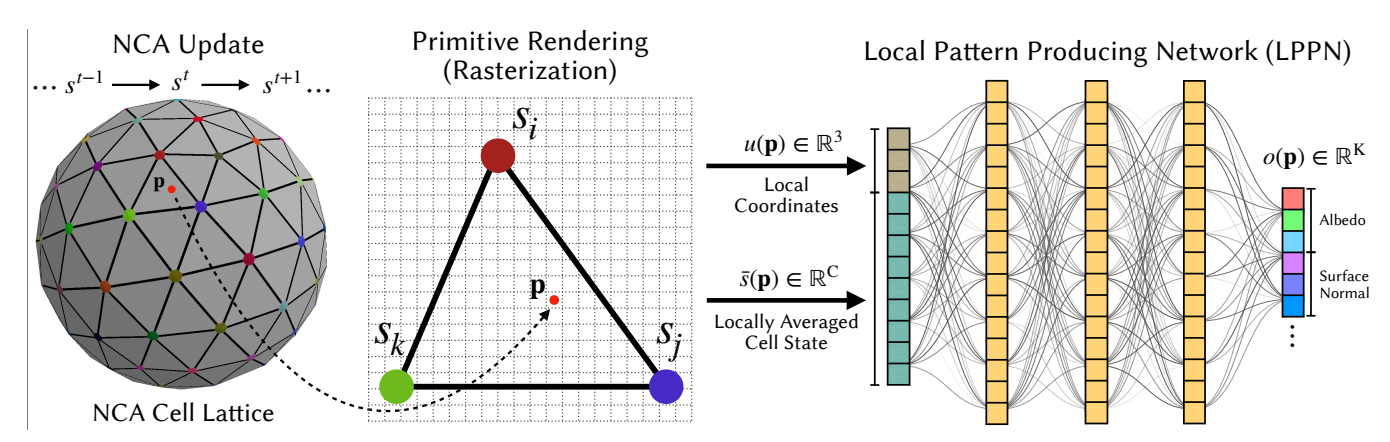* Left (左)：NCA 在粗糙的网格（三角形顶点）上运行。 * Center (中)：展示了一个采样点 $p$（红点）位于一个三角形图元内。 * $\bar{s}(p)$：通过插值顶点 $s^i, s^j, s^k$ 的状态得到局部平均状态。 * $u(p)$：点 $p$ 在三角形内的局部坐标。 * Right (右)：LPPN (MLP) 接收 $\bar{s}(p)$ 和 $u(p)$ 作为输入，输出该点的颜色等外观特征。

2.2 NCA：粗网格上的局部动力系统（“蓝图生成”）

NCA 是一个离散时间的局部更新系统：每一步先“感知邻居”，再用共享的神经网络更新自身状态。论文用一个抽象形式写为（原文 Eq. (1)）：

$$\mathbf{s}_{i}^{t+\Delta t} = \mathbf{s}_{i}^{t} + \mathcal{A}\big(\mathcal{Z}(\mathbf{s}_{i}^{t}, \mathbf{s}_{j}^{t})\big)\cdot \Delta t,\quad j \in \mathcal{N}(i).$$

这里： - $\mathcal{N}(i)$ 是邻域（例如 2D 网格的 3×3 邻域，mesh 的一环邻域）。 - $\mathcal{Z}(\cdot)$ 是 Perception（把邻域信息聚合成“感知向量”）。在 2D/3D 网格上通常是卷积；在 mesh 上可以是类似卷积的消息传递。 - $\mathcal{A}(\cdot)$ 是 Adaptation（一个小 MLP，把感知向量映射成状态增量）。

经过 $T$ 步演化后，我们得到粗网格上的状态场 $\{\mathbf{s}_i^T\}_{i=1}^N$。关键点：所有昂贵的“时序迭代”都只发生在粗分辨率上。

2.2 局部模式生成网络

LPPN ($f_{\theta}$) 独立地应用于每个采样点 $p$（即像素或 3D 位置），将其映射为输出属性（如 RGB 颜色）： $$o(\mathbf{p}) = f_{\theta}(\bar{s}(\mathbf{p}), u(\mathbf{p}))$$

LPPN 接收两个关键输入： * 局部平均细胞状态 ($\bar{s}(\mathbf{p})$)：通过对采样点 $p$ 周围图元 (Primitive) 内的细胞状态进行插值获得。这利用了 NCA 生成的宏观结构信息。 * 局部坐标 ($u(\mathbf{p})$)：编码了点 $p$ 在其所属图元内的相对位置。这提供了生成精细纹理所需的几何细节。

2.3 从“粗网格状态”到“连续点 $\mathbf{p}$”：图元 $\Omega$、$\lambda$-坐标与插值

LPPN 的第一个输入 $\bar{\mathbf{s}}(\mathbf{p})$ 需要把离散细胞状态“搬运”到连续点 $\mathbf{p}$。论文的做法是：对每个 $\mathbf{p}$，先确定一个包含它的 图元 (Primitive) $\Omega$（例如 2D 网格的一个矩形 cell、mesh 的一个三角形面片等），再用一组满足几何性质的权重 $\{\lambda_j(\mathbf{p})\}_{j\in\Omega}$ 进行插值。

对一个图元 $\Omega$，设其顶点（或角点）对应的细胞位置为 $\mathbf{v}^j$。$\lambda$-坐标要求满足三条性质（原文 “Partition of unity / Non-negativity / Linear precision”）： - 分割一致性：$\sum_{j\in\Omega}\lambda_j(\mathbf{p})=1$ - 非负性：$\lambda_j(\mathbf{p})\ge 0$ - 线性精度：$\mathbf{p}=\sum_{j\in\Omega}\lambda_j(\mathbf{p})\,\mathbf{v}^j$

有了 $\lambda$ 以后，就可以得到局部平均细胞状态（原文 Eq. (2)）：

$$\bar{\mathbf{s}}(\mathbf{p})=\sum_{j\in\Omega}\lambda_j(\mathbf{p})\,\mathbf{s}_j^T.$$

这一步对应 Figure 3 中间：红点 $\mathbf{p}$ 在三角形内部，用重心坐标（$\lambda$）对顶点细胞状态插值，得到 $\bar{\mathbf{s}}(\mathbf{p})$。

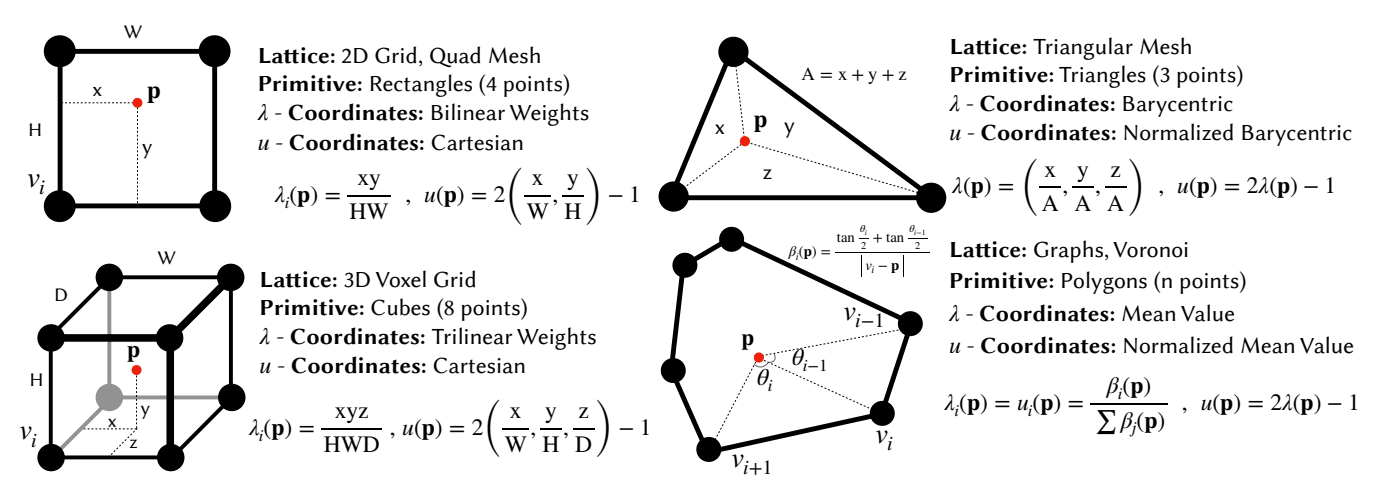
Figure 4: 图元类型（Primitives）

2.4 局部坐标 $u(\mathbf{p})$：让解码器知道“$\mathbf{p}$ 在图元里哪里”

如果只给 LPPN $\bar{\mathbf{s}}(\mathbf{p})$，它只能“看到”宏观结构，很难稳定地产生高频细节；因此还要提供 $\mathbf{p}$ 在图元内部的相对位置编码 $u(\mathbf{p})$。

论文的一个设计要点是：$u(\mathbf{p})$ 不一定等于原始的 $\lambda(\mathbf{p})$，而是一个更适合 MLP 学习的低维表示，并统一做零中心化：

• 矩形/立方体图元：用轴对齐笛卡尔坐标作为 $u(\mathbf{p})$（维度更低，直接表达“在格子里 x/y/z 的相对位置”）。
• 三角形/多边形图元（mesh）：保留 $\lambda(\mathbf{p})$（例如三角形的重心坐标）作为 $u(\mathbf{p})$。
• 统一 rescale：每一维都缩放到 $u(\mathbf{p})\in[-1,1]$（原始 $\lambda\in[0,1]$），避免输入偏置、便于训练。

2.5 关键细节：让 $u(\mathbf{p})$ “连续且均匀”（对应 Figure 5）

直接使用原始局部坐标会遇到两个问题： - 不连续：跨图元边界时，局部坐标会“重置/跳变”（图中中间列）。 - 分布不均：某些维度更常接近 1（或更常接近 0），导致输入动态范围不平衡、学习困难。

论文按图元类型给出两种处理：

1) 矩形/立方体图元：正弦基编码保证 $C^0$ 连续

对笛卡尔局部坐标向量 $u\in[-1,1]^d$，用前 $n$ 个谐波做特征扩展（原文给出的形式）：

$$u_{\text{aug}}=[\sin(\pi u),\cos(\pi u),\dots,\sin(n\pi u),\cos(n\pi u)].$$

直觉：$\sin/\cos$ 在边界处天然拼得更平滑，使得跨 cell 边界时的表示不“断裂”（Figure 5 右上）。

2) 三角形/多边形图元：排序消除顶点顺序依赖 + inverse-CDF 均衡动态范围

由于 mesh 邻面共享边，但顶点列举顺序可能不同，同一个几何位置在两个面上对应的 $\lambda$ 分量可能“交换”，造成不连续。解决： - 排序：对 $u(\mathbf{p})$ 的分量按降序排序，得到 $u_{\text{sort}}(\mathbf{p})$。这样“最大权重永远放在第 1 维”，跨面时更一致，从而达到 $C^0$ 连续（Figure 5 (a)）。 - inverse-CDF 重映射：排序后各分量的统计分布会非常不均（图里红色主导），于是对每一维做

$$u_{\text{cdf}}^{(k)}(\mathbf{p}) = 2\cdot F_k^{-1}\!\big(u_{\text{sort}}^{(k)}(\mathbf{p})\big)-1,$$

其中 $F_k^{-1}$ 是第 $k$ 维分量的（解析或经验）CDF 的逆函数，把值“拉伸”为近似均匀分布到 $[-1,1]$，从而均衡动态范围（Figure 5 (b)）。

局部坐标变换 (Local Coordinate Transformations)

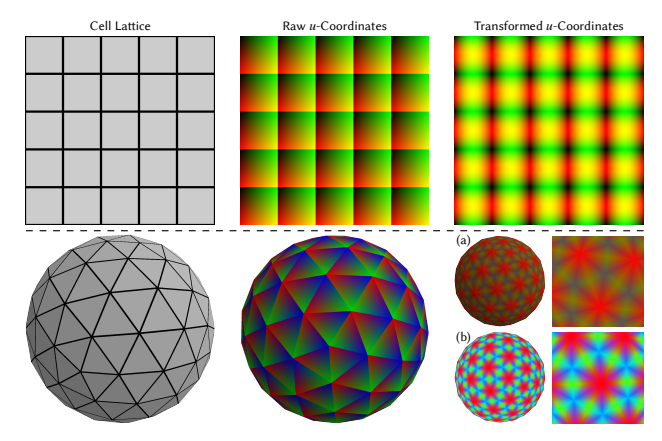* 问题：原始的局部坐标（如重心坐标）在图元边界处是不连续的，且分布不均匀（如红色主导）。 * 解决方案： * (a) 对坐标进行排序可以解决边界不连续问题，但导致动态范围不平衡。 * (b) 进一步应用 Inverse-CDF 重映射后，获得了既连续又均匀分布的坐标场（颜色分布更平滑），这更利于 LPPN 的学习。

2.6 LPPN：把 $(\bar{\mathbf{s}}(\mathbf{p}), u(\mathbf{p}))$ 解码成颜色/属性（“细节渲染”）

最终每个采样点 $\mathbf{p}$ 的输出由一个共享的小 MLP 给出（原文 Eq. (3)）：

$$\mathbf{o}(\mathbf{p})=f_{\theta}\!\big(\bar{\mathbf{s}}(\mathbf{p}),u(\mathbf{p})\big)\in\mathbb{R}^{K}.$$

注意这里的“共享”非常关键：同一个 $f_{\theta}$ 被对每个 $\mathbf{p}$ 重复调用，因此推理时可以高度并行；而且因为 NCA 的演化发生在粗网格上，整体成本被从“随输出分辨率平方增长”里解耦出来。

2.7 一个通用的训练目标写法（不绑定具体任务）

论文针对形态发生/纹理合成设计了更细的 loss（原文笔记里没展开细节）。但就“高分辨率监督”的通用形式，可以把 loss 写成对高分辨率采样点集合 $\mathcal{P}$ 的求和/期望：

$$\mathcal{L}=\mathbb{E}_{\mathbf{p}\sim \mathcal{P}}\Big[\ell\big(\mathbf{o}(\mathbf{p}),\mathbf{y}(\mathbf{p})\big)\Big],\quad \mathbf{o}(\mathbf{p})=f_{\theta}\!\big(\bar{\mathbf{s}}(\mathbf{p}),u(\mathbf{p})\big).$$

其中 $\mathbf{y}(\mathbf{p})$ 是目标图像/纹理在位置 $\mathbf{p}$ 的真值，$\ell$ 可以是 $L_1/L_2$、感知损失等。关键是：你可以把 $\mathcal{P}$ 选得很密（渲染超高分辨率），但 NCA 演化仍然只在粗网格上进行。

3. 实验

作者在多种 NCA 变体和任务上验证了该方法的有效性：

1. 形态发生 (Morphogenesis)：

   • 任务：从单个种子细胞生长出目标 2D 形状或图像。
   • 结果：能够生成高保真的图像，且具有再生能力。

2. 纹理合成 (Texture Synthesis)：

   • 2D 纹理：在平面上合成动态纹理。
   • 3D 网格纹理：利用 Mesh NCA 在任意拓扑的 3D 模型表面合成纹理。
   • 优势：能够在保持 NCA 模拟网格较小的情况下，生成非常精细的表面细节。

4. 结果与讨论

• 高质量与高分辨率：该方法使得 NCA 能够生成 1024x1024 甚至更高分辨率的输出（如 Figure 2 所示），而无需在如此大的网格上运行昂贵的 NCA 更新步骤。

混合模型输出示例 (Sample Output)

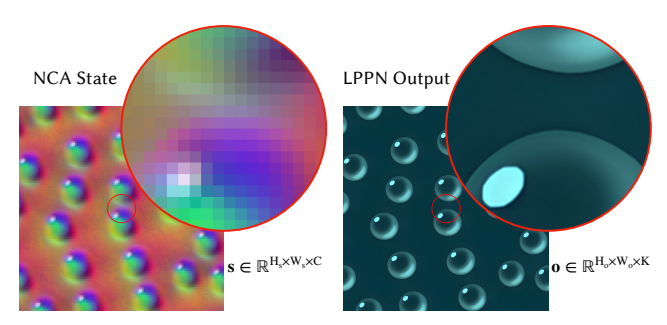* 内容：对比了 NCA 的模拟分辨率与最终输出分辨率。 * 细节：NCA 实际上是在一个粗糙的 $128 \times 128$ 格子上演化的。然而，通过 LPPN，模型可以渲染出 $1024 \times 1024$ 的 RGB 图像。 * 插图 (Inset)：右侧放大的眼睛区域展示了即使在 $8192 \times 8192$ 的超高分辨率下，模型依然能保持清晰度（无需重新训练），体现了隐式表示的优势。

• 计算效率：由于 NCA 逻辑仅在粗糙网格上运行，训练和推理极其高效。LPPN 仅在渲染时调用，且各像素计算独立，高度可并行化。
• 保持涌现特性：混合模型并未牺牲 NCA 的核心优势。系统依然表现出鲁棒性（对干扰的抵抗力）、自修复能力以及对未见环境的泛化能力。

5. 个人评价

就我个人来看，这篇论文本质上就是拿一个自动细胞器生成一个分辨率比较小的图片，然后把它用插值映射到了一个大图片。不是什么很大的创新工作，但同样值得学习。