Natural Evolution Strategies (NES)
作者: Daan Wierstra, Tom Schaul, Tobias Glasmachers, Yi Sun, Jürgen Schmidhuber
论文链接: http://arxiv.org/abs/1106.4487v1
被引用：1246（来自谷歌学术）
1. 简介 (Introduction)
Natural Evolution Strategies (NES) 是一类黑盒优化算法，它通过维护一个参数化的搜索分布，并利用自然梯度（Natural Gradient）朝着期望适应度（Expected Fitness）更高的方向更新分布参数。
NES 的核心思想是：不直接维护一组搜索点（种群），而是维护并迭代更新一个搜索分布。从该分布中采样搜索点并评估其适应度，然后利用这些信息估计分布参数上的搜索梯度。NES 执行沿着自然梯度的梯度上升步骤。自然梯度是一种二阶方法，它根据不确定性对更新进行重归一化，从而避免了普通梯度的振荡和过早收敛问题。
2. 搜索梯度 (Search Gradients)
NES 的核心是使用搜索梯度来更新搜索分布的参数。 设 $\pi(\mathbf{z} \mid \theta)$ 表示参数为 $\theta$ 的搜索分布，$f(\mathbf{z})$ 为样本 $\mathbf{z}$ 的适应度函数。 在搜索分布下的期望适应度为：
$$J(\theta) = \mathbb{E}_{\theta}[f(\mathbf{z})] = \int f(\mathbf{z}) \, \pi(\mathbf{z} \,|\, \theta) \, d\mathbf{z} \tag{1}$$
利用 "对数似然技巧" (log-likelihood trick)，我们可以推导梯度的公式：
$$ \begin{aligned} \nabla_{\theta} J(\theta) &= \nabla_{\theta} \int f(\mathbf{z}) \ \pi(\mathbf{z} \mid \theta) \ d\mathbf{z} \\ &= \int f(\mathbf{z}) \ \nabla_{\theta} \pi(\mathbf{z} \mid \theta) \ d\mathbf{z} \\ &= \int f(\mathbf{z}) \ \nabla_{\theta} \pi(\mathbf{z} \mid \theta) \ \frac{\pi(\mathbf{z} \mid \theta)}{\pi(\mathbf{z} \mid \theta)} \ d\mathbf{z} \\ &= \int \left[ f(\mathbf{z}) \ \nabla_{\theta} \log \pi(\mathbf{z} \mid \theta) \right] \pi(\mathbf{z} \mid \theta) \ d\mathbf{z} \\ &= \mathbb{E}_{\theta} \left[ f(\mathbf{z}) \ \nabla_{\theta} \log \pi(\mathbf{z} \mid \theta) \right] \end{aligned} $$
通过蒙特卡洛采样 $\mathbf{z}_1 \dots \mathbf{z}_{\lambda}$，我们可以得到搜索梯度的估计值：
$$\nabla_{\theta} J(\theta) \approx \frac{1}{\lambda} \sum_{k=1}^{\lambda} f(\mathbf{z}_k) \, \nabla_{\theta} \log \pi(\mathbf{z}_k \mid \theta) \tag{2}$$
其中 $\lambda$ 是种群大小。
Algorithm 1: Canonical Search Gradient algorithm
input: f, theta_init
repeat
for k = 1 ... lambda do
draw sample z_k ~ pi(.|theta)
evaluate the fitness f(z_k)
calculate log-derivatives grad_theta log pi(z_k|theta)
end
grad_theta J <- 1/lambda * sum(grad_theta log pi(z_k|theta) * f(z_k))
theta <- theta + eta * grad_theta J
until stopping criterion is met
2.1 高斯分布的搜索梯度 (Search Gradient for Gaussian Distributions)
对于 $d$ 维多元正态分布，参数 $\theta = \langle \boldsymbol{\mu}, \boldsymbol{\Sigma} \rangle$。 为了高效采样，令 $\boldsymbol{\Sigma} = \mathbf{A}^{\top} \mathbf{A}$。 采样过程：$\mathbf{z} = \boldsymbol{\mu} + \mathbf{A}^{\top} \mathbf{s}$，其中 $\mathbf{s} \sim \mathcal{N}(0, \mathbb{I})$。
概率密度函数为： $$\pi(\mathbf{z} \mid \theta) = \frac{1}{\sqrt{(2\pi)^d \det(\boldsymbol{\Sigma})}} \cdot \exp\left(-\frac{1}{2} (\mathbf{z} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\mathbf{z} - \boldsymbol{\mu})\right)$$
对数似然的导数为：
$$\nabla_{\mu} \log \pi \left( \mathbf{z} | \theta \right) = \mathbf{\Sigma}^{-1} \left( \mathbf{z} - \boldsymbol{\mu} \right) \tag{3}$$
$$\nabla_{\Sigma} \log \pi \left( \mathbf{z} | \theta \right) = \frac{1}{2} \Sigma^{-1} \left( \mathbf{z} - \boldsymbol{\mu} \right) \left( \mathbf{z} - \boldsymbol{\mu} \right)^{\top} \Sigma^{-1} - \frac{1}{2} \Sigma^{-1} \tag{4}$$
2.2 普通搜索梯度的局限性 (Limitations of Plain Search Gradients)
普通梯度在定位最优解时存在不稳定性。例如在 $d=1$ 时，$\sigma$ 越小，更新的方差越大 ($\Delta \mu \propto 1/\sigma$, $\Delta \sigma \propto 1/\sigma$)，导致在接近最优解时（$\sigma$ 应该很小）更新步长变得非常大且不稳定。 如下图所示：
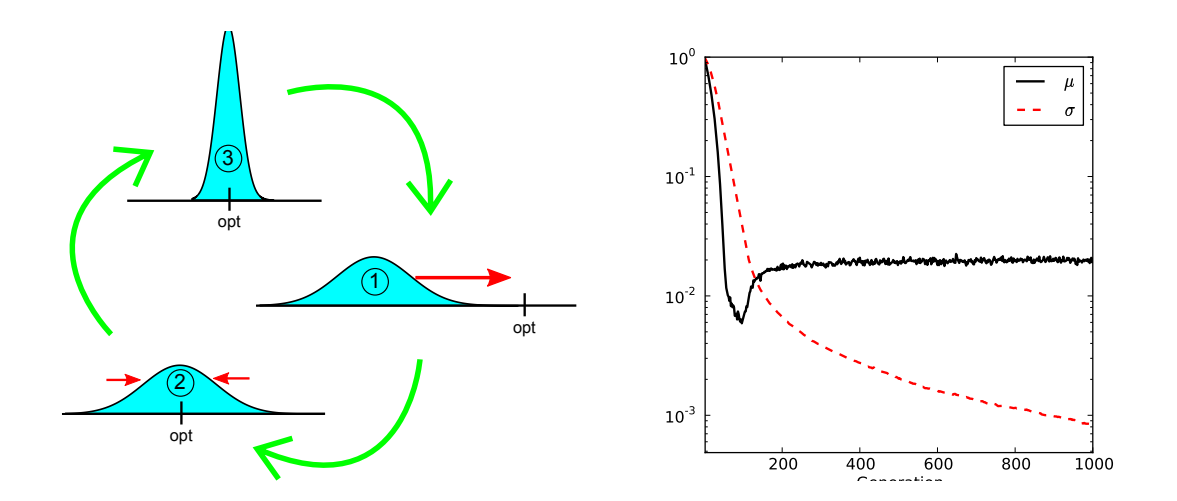
图 1: 左图展示了普通梯度在 $\sigma$ 变小时导致的过冲现象。右图展示了在最小化 $f(z)=z^2$ 时 $\mu$ 和 $\sigma$ 的变化，即使使用很小的学习率也难以精确定位。
3. 自然梯度 (Natural Gradient)
为了解决普通梯度的参数依赖和不稳定性问题，NES 采用自然梯度。自然梯度基于概率分布之间的 Kullback-Leibler 散度 (KL divergence) 来定义参数空间中的距离，而不是欧几里得距离。
自然梯度定义为以下约束优化问题的解：
$$\max_{\delta\theta} J(\theta + \delta\theta) \approx J(\theta) + \delta\theta^{\top} \nabla_{\theta} J$$ $$\text{s.t. } D(\theta + \delta\theta || \theta) = \varepsilon$$
其中 $D$ 是 KL 散度。当 $\delta\theta \to 0$ 时，$D(\theta + \delta\theta || \theta) \approx \frac{1}{2} \delta\theta^{\top} \mathbf{F}(\theta) \delta\theta$，其中 $\mathbf{F}$ 是 Fisher 信息矩阵 (Fisher Information Matrix)：
$$\mathbf{F} = \mathbb{E} \left[ \nabla_{\theta} \log \pi \left( \mathbf{z} | \theta \right) \nabla_{\theta} \log \pi \left( \mathbf{z} | \theta \right)^{\top} \right]$$
自然梯度的方向 $\widetilde{\nabla}_{\theta} J$ 为：
$$\widetilde{\nabla}_{\theta} J = \mathbf{F}^{-1} \nabla_{\theta} J(\theta)$$
Fisher 矩阵也可以从样本中估计。
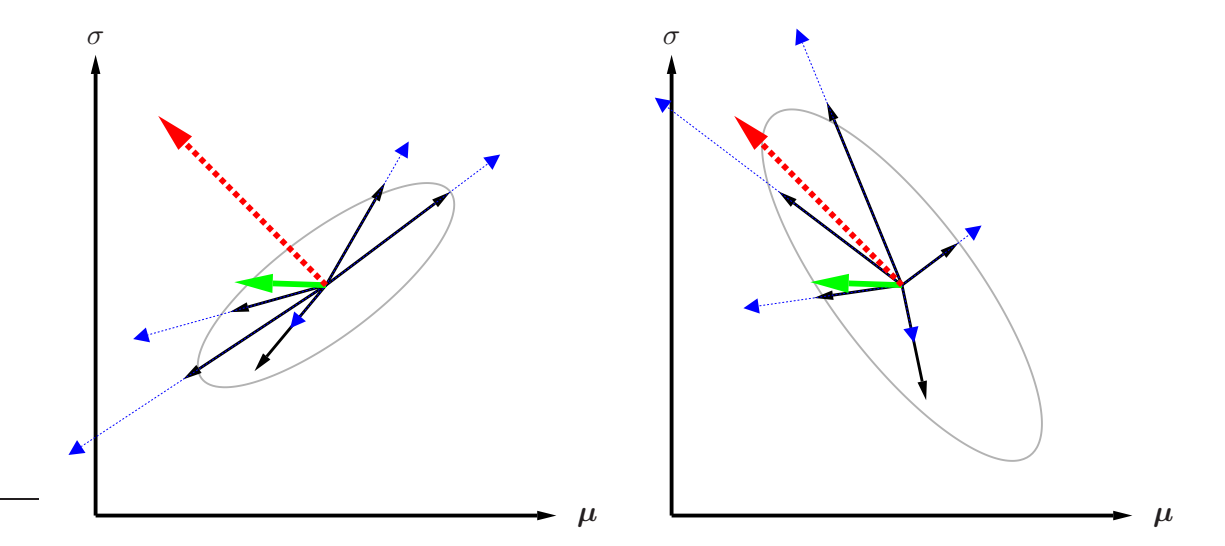图 2: 普通梯度（绿色）与自然梯度（红色虚线）的对比。Fisher 矩阵修正了协方差（灰色椭圆），使得自然梯度在不确定性较高的方向上减小步长，而在确定性较高的方向上增大步长。
Algorithm 3: Canonical Natural Evolution Strategies
input: f, theta_init
repeat
for k = 1 ... lambda do
draw sample z_k ~ pi(.|theta)
evaluate f(z_k)
calculate log-derivatives grad_theta log pi(z_k|theta)
end
grad_theta J <- 1/lambda * sum(grad_theta log pi(z_k|theta) * f(z_k))
F <- 1/lambda * sum(grad_theta log pi(z_k|theta) * grad_theta log pi(z_k|theta)^T)
theta <- theta + eta * F^-1 * grad_theta J
until stopping criterion is met
4. 性能与鲁棒性技术 (Performance and Robustness Techniques)
3.1 适应度重塑 (Fitness Shaping)
为了使算法对适应度函数的单调变换具有不变性，NES 使用基于排名的适应度重塑。将适应度转换为一组效用值 (utility values) $u_1 \ge \dots \ge u_{\lambda}$。 令 $\mathbf{z}_i$ 表示第 $i$ 好的个体。梯度估计变为：
$$\nabla_{\theta} J(\theta) = \sum_{k=1}^{\lambda} u_k \, \nabla_{\theta} \log \pi(\mathbf{z}_k \,|\, \theta) \tag{6}$$
要求 $\sum |u_k| = 1$。常用的效用函数（类似于 CMA-ES）： $u_k = \frac{\max(0, \log(\frac{\lambda}{2} + 1) - \log(i))}{\sum_{j=1}^{\lambda} \max(0, \log(\frac{\lambda}{2} + 1) - \log(j))} - \frac{1}{\lambda}$
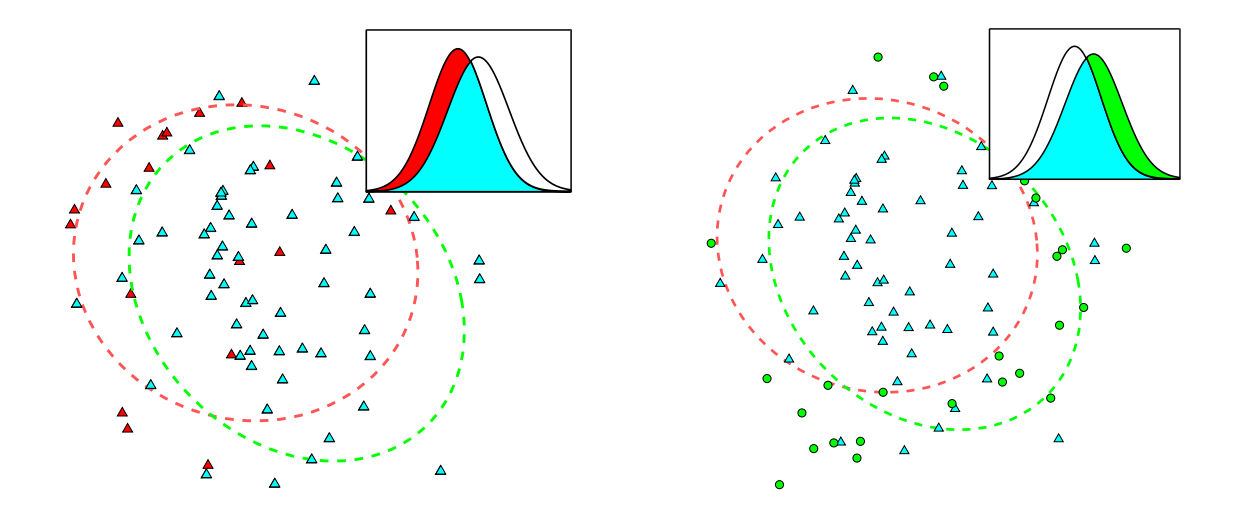
3.2 重要性混合 (Importance Mixing)
为了减少适应度评估的次数，利用重要性采样重用前一代的样本。 1. 拒绝采样 (Rejection Sampling)：从旧批次中保留样本 $\mathbf{z}$，接受概率为 $\min \{ 1, (1 - \alpha) \frac{\pi(\mathbf{z} | \theta)}{\pi(\mathbf{z} | \theta')} \}$。 2. 反向拒绝采样 (Reverse Rejection Sampling)：生成新样本 $\mathbf{z}$，接受概率为 $\max \{ \alpha, 1 - \frac{\pi(\mathbf{z} | \theta')}{\pi(\mathbf{z} | \theta)} \}$，直到填满种群。
3.3 自适应采样 (Adaptation Sampling)
一种在线调整学习率 $\eta$ 的元学习方法。通过假设一个新的学习率 $\eta' = 1.5\eta$ 生成虚拟分布，并使用加权 Mann-Whitney U 检验比较新旧分布样本的质量。如果改进显著，则增加学习率；否则衰减。
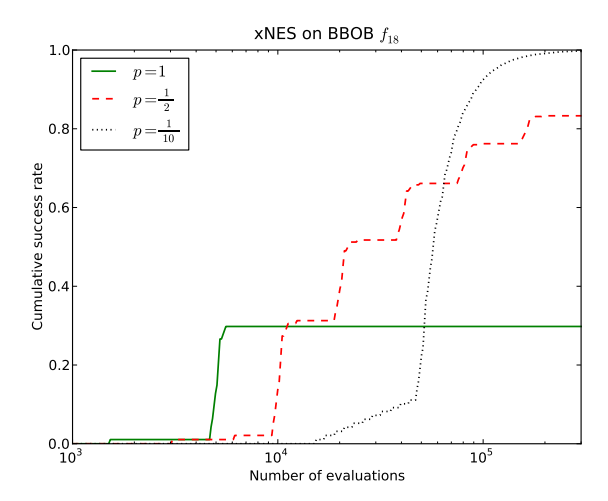
3.4 重启策略 (Restart Strategies)
为了应对多模态问题，采用重启策略。将总时间预算的一定比例 $p$ 分配给第一次运行，剩余 $1-p$ 时间递归分配。随着时间推移，尝试更多不同种子的运行。
5. 多元正态分布技术 (Techniques for Multinormal Distributions)
对于多元正态分布，直接计算 Fisher 矩阵的逆极其昂贵 ($\mathcal{O}(d^6)$)。本节介绍两种关键技术。
4.1 指数参数化 (Exponential Parameterization)
为了保证协方差矩阵 $\Sigma$ 的正定性，使用指数映射表示 $\Sigma$： $\Sigma = \exp(\mathbf{M})$，其中 $\mathbf{M} \in \mathcal{S}_d$ (对称矩阵空间)。 更新 $\mathbf{M}$ 保证了 $\Sigma$ 始终在正定对称矩阵流形 $\mathcal{P}_d$ 上。
4.2 自然坐标系 (Natural Coordinates)
为了避免显式计算 Fisher 矩阵，我们在每次迭代中移动坐标系，使得当前的搜索分布变为标准正态分布（零均值，单位协方差）。 在自然坐标系中，Fisher 矩阵为单位矩阵 $\mathbb{I}$，因此自然梯度等于普通梯度。
设当前分布为 $\mathcal{N}(\boldsymbol{\mu}, \mathbf{A}^{\top}\mathbf{A})$。 更新后的分布表示为： $$(\boldsymbol{\mu}_{\text{new}}, \mathbf{A}_{\text{new}}) = \left(\boldsymbol{\mu} + \mathbf{A}^{\top} \boldsymbol{\delta}, \mathbf{A} \exp\left(\frac{1}{2}\mathbf{M}\right)\right) \tag{10}$$
在自然坐标系 ($\boldsymbol{\delta}=0, \mathbf{M}=0$) 下的对数导数非常简单：
$$\nabla_{\boldsymbol{\delta}} \log \pi(\mathbf{z}) = \mathbf{s} \tag{11}$$ $$\nabla_{\mathbf{M}} \log \pi(\mathbf{z}) = \frac{1}{2} (\mathbf{s}\mathbf{s}^{\top} - \mathbb{I}) \tag{12}$$
其中 $\mathbf{s} = \mathbf{A}^{-\top}(\mathbf{z} - \boldsymbol{\mu})$ 是标准正态分布样本。
因此，自然梯度的更新规则为：
$$\nabla_{\delta} J = \sum_{k=1}^{\lambda} f(\mathbf{z}_k) \cdot \mathbf{s}_k \tag{13}$$ $$\nabla_{\mathbf{M}} J = \sum_{k=1}^{\lambda} f(\mathbf{z}_k) \cdot (\mathbf{s}_k \mathbf{s}_k^{\top} - \mathbb{I}) \tag{14}$$
4.3 参数空间的分解与 xNES (Exponential NES)
将 $\mathbf{M}$ 分解为迹（步长 $\sigma$）和迹为0的部分（形状 $\mathbf{B}$）。 $\mathbf{A} = \sigma \cdot \mathbf{B}$，其中 $\det(\mathbf{B})=1$。
更新规则 (xNES)：
$$\boldsymbol{\mu}_{\text{new}} \leftarrow \boldsymbol{\mu} + \eta_{\delta} \cdot \sigma \mathbf{B} \cdot \nabla_{\delta} J \tag{16}$$ $$\sigma_{\text{new}} \leftarrow \sigma \cdot \exp\left(\frac{\eta_{\sigma}}{2} \cdot \frac{\operatorname{tr}(\nabla_{\mathbf{M}}J)}{d}\right) \tag{17}$$ $$\mathbf{B}_{\text{new}} \leftarrow \mathbf{B} \cdot \exp\left(\frac{\eta_{\mathbf{B}}}{2} \cdot \left(\nabla_{\mathbf{M}} J - \frac{\operatorname{tr}(\nabla_{\mathbf{M}} J)}{d} \cdot \mathbb{I}\right)\right) \tag{18}$$
如果 $\eta_{\sigma} = \eta_{\mathbf{B}} = \eta_{\mathbf{A}}$，则更新合并为： $$\mathbf{A}_{\text{new}} \leftarrow \mathbf{A} \cdot \exp\left(\frac{\eta_{\mathbf{A}}}{2} \cdot \nabla_{\mathbf{M}} J\right) \tag{19}$$
Algorithm 4: Exponential Natural Evolution Strategies (xNES)
input: f, mu_init, Sigma_init = A^T A
initialize sigma <- det(A)^(1/d), B <- A/sigma
repeat
for k = 1 ... lambda do
draw sample s_k ~ N(0, I)
z_k <- mu + sigma * B^T * s_k
evaluate f(z_k)
end
compute utilities u_k based on sorted fitness
grad_delta J <- sum(u_k * s_k)
grad_M J <- sum(u_k * (s_k * s_k^T - I))
grad_sigma J <- tr(grad_M J) / d
grad_B J <- grad_M J - grad_sigma J * I
mu <- mu + eta_delta * sigma * B * grad_delta J
sigma <- sigma * exp(eta_sigma/2 * grad_sigma J)
B <- B * exp(eta_B/2 * grad_B J)
until stopping criterion is met
Algorithm 5: (1+1)-xNES (Hill-climber variant)
适用于单样本（精英策略）的版本。使用成功/失败的离散效用值来近似 1/5 成功法则。
6. 可分离 NES (Separable NES, SNES)
对于高维问题 ($d$ 很大)，全协方差矩阵更新 $\mathcal{O}(d^3)$ 过于昂贵。SNES 限制协方差矩阵为对角矩阵（即可分离分布）。 这将复杂度降低到 $\mathcal{O}(d)$。
Algorithm 7: Separable NES (SNES)
input: f, mu_init, sigma_init (vector)
repeat
for k = 1 ... lambda do
draw sample s_k ~ N(0, I)
z_k <- mu + sigma * s_k (element-wise product)
evaluate f(z_k)
end
compute utilities u_k
grad_mu J <- sum(u_k * s_k)
grad_sigma J <- sum(u_k * (s_k^2 - 1))
mu <- mu + eta_mu * sigma * grad_mu J
sigma <- sigma * exp(eta_sigma/2 * grad_sigma J)
until stopping criterion is met
7. 重尾分布 NES (Heavy-tailed NES)
为了更好地跳出局部最优，可以使用重尾分布（如柯西分布）。 对于一般旋转对称分布，利用自然坐标系，我们不需要显式计算 Fisher 矩阵。
5.3.2 柯西分布 (Cauchy Distributions)
对于多元柯西分布，梯度分量为：
$$\nabla_{\boldsymbol{\delta}} J = \frac{d+1}{\|\mathbf{s}\|^2 + 1} \cdot \mathbf{s}$$ $$\nabla_{\mathbf{M}} J = \frac{d+1}{2 \cdot (\|\mathbf{s}\|^2 + 1)} \cdot \mathbf{s} \mathbf{s}^{\top} - \frac{1}{2} \cdot \mathbb{I}$$
Algorithm 8: (1+1)-NES with multi-variate Cauchy distribution
input: f, mu_init, A_init
repeat
draw s ~ N(0, I)
draw r ~ Cauchy(0, 1)
z <- mu + r * A^T * s
... (evaluate and update using Cauchy gradients) ...
until stopping criterion is met
8. 实验结论 (Experiments Summary)
- xNES 在标准基准测试中表现出与 CMA-ES 相当甚至更强的鲁棒性。
- SNES 在高维可分离问题（如神经进化控制任务）中表现出色，具有线性复杂度。
- Cauchy-NES 在具有欺骗性局部最优的全局优化问题中，利用其长尾特性更容易跳出局部最优。
- 重启策略 和 适应度采样 显著提高了多模态和噪声环境下的成功率。
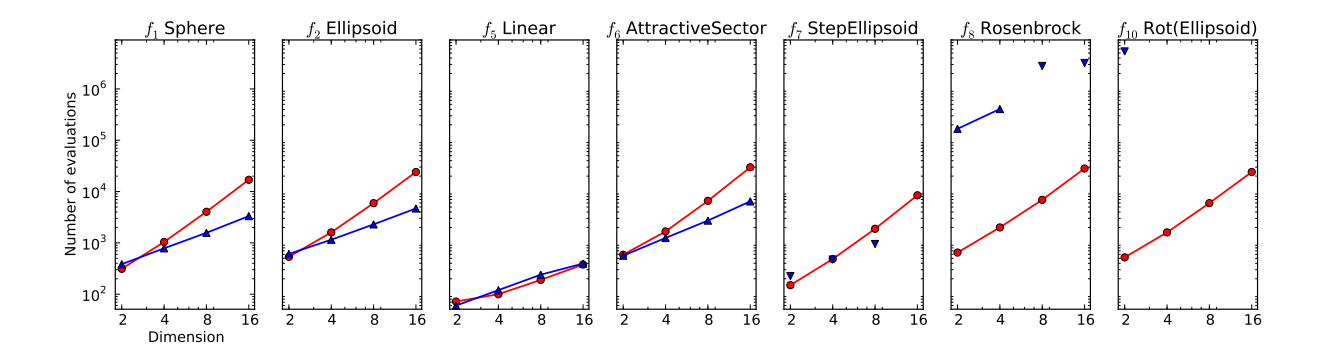图 11: xNES 与 SNES 在单模态基准上的对比。SNES 在可分离问题 ($f_1-f_6$) 上极快，但在非可分离问题 ($f_{10}$) 上失败。
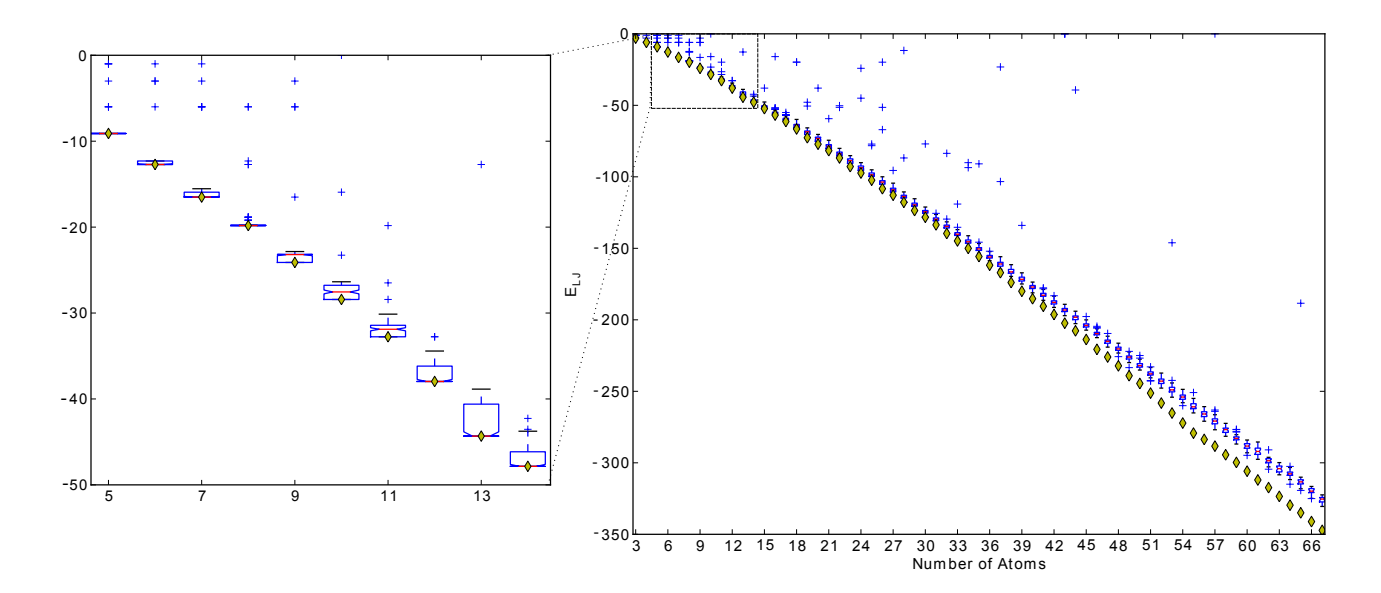图 14: SNES 在 Lennard-Jones 原子簇势能最小化问题上的表现，展示了其扩展到数百维参数的能力。