title: The CMA Evolution Strategy: A Tutorial url: http://arxiv.org/abs/1604.00772v2
The CMA Evolution Strategy: A Tutorial
Nikolaus Hansen Inria Research centre Saclay– ˆIle-de-France
Contents
| Nomenclature | 2 | |
|---|---|---|
| 0 | Preliminaries 0.1 Eigendecomposition of a Positive Definite Matrix 0.2 The Multivariate Normal Distribution 0.3 Randomized Black Box Optimization 0.4 Hessian and Covariance Matrices |
3 4 5 6 7 |
| 1 | Basic Equation: Sampling | 8 |
| 2 | Selection and Recombination: Moving the Mean | 8 |
| 3 | Adapting the Covariance Matrix 3.1 Estimating the Covariance Matrix From Scratch µ-Update 3.2 Rank 3.3 Rank-One-Update 3.3.1 A Different Viewpoint 3.3.2 Cumulation: Utilizing the Evolution Path µ-Update and Cumulation 3.4 Combining Rank |
10 10 12 15 15 16 18 |
| 4 | Step-Size Control | 19 |
| 5 | Discussion | 22 |
| A | Algorithm Summary: The CMA-ES | 28 |
| B | Implementational Concerns B.1 Multivariate normal distribution B.2 Strategy internal numerical effort B.3 Termination criteria B.4 Flat fitness B.5 Boundaries and Constraints |
32 33 33 33 34 34 |
| C | MATLAB Source Code | 36 |
| D | ccov Reformulation of Learning Parameter |
38 |
Compiled March 13, 2023
Nomenclature
We adopt the usual vector notation, where bold letters, v, are column vectors, capital bold letters, A, are matrices, and a transpose is denoted by v T. A list of used abbreviations and symbols is given in alphabetical order.
Abbreviations
CMA Covariance Matrix Adaptation
EMNA Estimation of Multivariate Normal Algorithm
ES Evolution Strategy
(µ/µ{I,W}, λ)-ES, Evolution Strategy with µ parents, with recombination of all µ parents, either Intermediate or Weighted, and λ offspring.
RHS Right Hand Side.
Greek symbols
λ ≥ 2, population size, sample size, number of offspring, see (5).
µ ≤ λ parent number, number of (positively) selected search points in the population, number of strictly positive recombination weights, see (6).
µeff = P^{µ} i=1 w 2 i −1 , the variance effective selection mass for the mean, see (8).
Pw^{j} = P^{λ} i=1 w^{i} , sum of all weights, note that w^{i} ≤ 0 for i > µ, see also (30) and (53).
P|w^{i} + = P^{µ} i=1 w^{i} = 1, sum of all positive weights.
P|w^{i} | − = −( Pw^{j} − P|w^{i} | +) = − P^{λ} i=µ+1 w^{i} ≥ 0, minus the sum of all negative weights.
σ (g) ∈ R>0, step-size.
Latin symbols
B ∈ R n, an orthogonal matrix. Columns of B are eigenvectors of C with unit length and correspond to the diagonal elements of D.
C(g) ∈ R n×n, covariance matrix at generation g.
cii, diagonal elements of C.
c^{1} ≤ 1 − cµ, learning rate for the rank-one update of the covariance matrix update, see (28), (30), and (47), and Table 1.
c^{µ} ≤ 1 − c1, learning rate for the rank-µ update of the covariance matrix update, see (16), (30), and (47), and Table 1.
c^{σ} < 1, decay rate for the cumulation path for the step-size control, see (31) and (43), and Table 1.
c^{c} ≤ 1, decay rate for cumulation path for the rank-one update of the covariance matrix, see (24) and (45), and Table 1.
$c_{\rm m}=1$ , learning rate for the mean.
$D \in \mathbb{R}^n$ , a diagonal matrix. The diagonal elements of D are square roots of eigenvalues of C and correspond to the respective columns of B.
$d_i > 0$ , diagonal elements of diagonal matrix D, $d_i^2$ are eigenvalues of C.
$d_{\sigma} \approx 1$ , damping parameter for step-size update, see (32), (37), and (44).
E Expectation value
$f: \mathbb{R}^n \to \mathbb{R}, \boldsymbol{x} \mapsto f(\boldsymbol{x})$ , objective function (fitness function) to be minimized.
$$f_{\text{sphere}}: \mathbb{R}^n \to \mathbb{R}, \boldsymbol{x} \mapsto \|\boldsymbol{x}\|^2 = \boldsymbol{x}^\mathsf{T} \boldsymbol{x} = \sum_{i=1}^n x_i^2.$$
$g \in \mathbb{N}_0$ , generation counter, iteration number.
$\mathbf{I} \in \mathbb{R}^{n \times n}$ , Identity matrix, unity matrix.
$m^{(g)} \in \mathbb{R}^n$ , mean value of the search distribution at generation g.
$n \in \mathbb{N}$ , search space dimension, see f.
$\mathcal{N}(\mathbf{0}, \mathbf{I})$ , multivariate normal distribution with zero mean and unity covariance matrix. A vector distributed according to $\mathcal{N}(\mathbf{0}, \mathbf{I})$ has independent, (0, 1)-normally distributed components.
$\mathcal{N}(m,C) \sim m + \mathcal{N}(0,C)$ , multivariate normal distribution with mean $m \in \mathbb{R}^n$ and covariance matrix $C \in \mathbb{R}^{n \times n}$ . The matrix C is symmetric and positive definite.
$\mathbb{R}_{>0}$ , strictly positive real numbers.
$p \in \mathbb{R}^n$ , evolution path, a sequence of successive (normalized) steps, the strategy takes over a number of generations.
$w_i$ , where $i = 1, \dots, \lambda$ , recombination weights, see (6) and (16) and (49)–(53).
$x_k^{(g+1)} \in \mathbb{R}^n$ , k-th offspring/individual from generation g+1. We also refer to $x^{(g+1)}$ , as search point, or object parameters/variables, commonly used synonyms are candidate solution, or design variables.
$m{x}_{i:\lambda}^{(g+1)}, i$ -th best individual out of $m{x}_1^{(g+1)}, \dots, m{x}_{\lambda}^{(g+1)}$ , see (5). The index $i:\lambda$ denotes the index of the i-th ranked individual and $f(m{x}_{1:\lambda}^{(g+1)}) \leq f(m{x}_{2:\lambda}^{(g+1)}) \leq \dots \leq f(m{x}_{\lambda:\lambda}^{(g+1)})$ , where f is the objective function to be minimized.
$$m{y}_k^{(g+1)} = (m{x}_k^{(g+1)} - m{m}^{(g)})/\sigma^{(g)}$$ corresponding to $m{x}_k = m{m} + \sigma m{y}_k$ .
0 Preliminaries
This tutorial introduces the CMA Evolution Strategy (ES), where CMA stands for Covariance Matrix Adaptation.1 The CMA-ES is a stochastic, or randomized, method for real-parameter (continuous domain) optimization of non-linear, non-convex functions (see also Section 0.3
<sup>1Parts of this material have also been presented in [15] and [17], in the context of Estimation of Distribution Algorithms and Adaptive Encoding, respectively. An introduction deriving CMA-ES from the information-geometric concept of a natural gradient can be found in [19].
below).2 We try to motivate and derive the algorithm from intuitive concepts and from requirements of non-linear, non-convex search in continuous domain. For a concise algorithm description see Appendix A. A respective Matlab source code is given in Appendix C.
Before we start to introduce the algorithm in Sect. 1, a few required fundamentals are summed up.
0.1 Eigendecomposition of a Positive Definite Matrix
A symmetric, positive definite matrix, $C \in \mathbb{R}^{n \times n}$ , is characterized in that for all $x \in \mathbb{R}^n \setminus \{0\}$ holds $x^T C x > 0$ . The matrix C has an orthonormal basis of eigenvectors, $B = [b_1, \dots, b_n]$ , with corresponding eigenvalues, $d_1^2, \dots, d_n^2 > 0$ .
That means for each $b_i$ holds
$$Cb_i = d_i^2 b_i . (1)$$
The important message from (1) is that eigenvectors are not rotated by C. This feature uniquely distinguishes eigenvectors. Because we assume the orthogonal eigenvectors to be of unit length, $\boldsymbol{b}_i^\mathsf{T} \boldsymbol{b}_j = \delta_{ij} = \left\{ \begin{array}{ll} 1 & \text{if } i = j \\ 0 & \text{otherwise} \end{array} \right.$ , and $\boldsymbol{B}^\mathsf{T} \boldsymbol{B} = \mathbf{I}$ (obviously this means $\boldsymbol{B}^{-1} = \boldsymbol{B}^\mathsf{T}$ , and it follows $\boldsymbol{B}\boldsymbol{B}^\mathsf{T} = \mathbf{I}$ ). An basis of eigenvectors is practical, because for any $\boldsymbol{v} \in \mathbb{R}^n$ we can find coefficients $\alpha_i$ , such that $\boldsymbol{v} = \sum_i \alpha_i \boldsymbol{b}_i$ , and then we have $C\boldsymbol{v} = \sum_i d_i^2 \alpha_i \boldsymbol{b}_i$ .
The eigendecomposition of C obeys
$$C = BD^2B^{\mathsf{T}} \tag{2}$$
where
B is an orthogonal matrix, $B^{\mathsf{T}}B = BB^{\mathsf{T}} = \mathbf{I}$ . Columns of B form an orthonormal basis of eigenvectors.
$D^2 = DD = \operatorname{diag}(d_1, \dots, d_n)^2 = \operatorname{diag}(d_1^2, \dots, d_n^2)$ is a diagonal matrix with eigenvalues of C as diagonal elements.
$D = diag(d_1, ..., d_n)$ is a diagonal matrix with square roots of eigenvalues of C as diagonal elements.
The matrix decomposition (2) is unique, apart from signs of columns of B and permutations of columns in B and $D^2$ respectively, given all eigenvalues are different.3
Given the eigendecomposition (2), the inverse $C^{-1}$ can be computed via
$$C^{-1} = (BD^{2}B^{\mathsf{T}})^{-1}$$
$$= B^{\mathsf{T}^{-1}}D^{-2}B^{-1}$$
$$= BD^{-2}B^{\mathsf{T}}$$
$$= B\operatorname{diag}\left(\frac{1}{d_{1}^{2}}, \dots, \frac{1}{d_{n}^{2}}\right)B^{\mathsf{T}}.$$
<sup>2While CMA variants for multi-objective optimization and elitistic variants have been proposed, this tutorial is solely dedicated to single objective optimization and non-elitistic truncation selection, also referred to as commaselection.
<sup>3Given m eigenvalues are equal, any orthonormal basis of their m-dimensional subspace can be used as column vectors. For m > 1 there are infinitely many such bases.
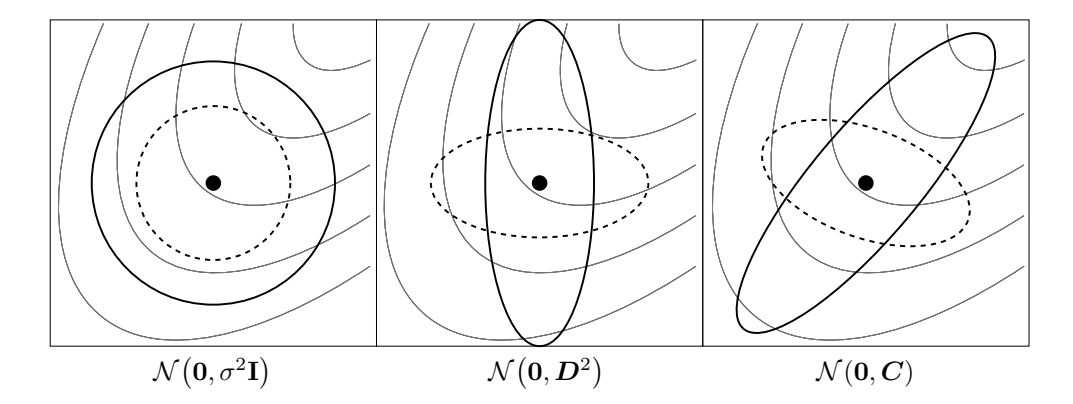
Figure 1: Ellipsoids depicting one- $\sigma$ lines of equal density of six different normal distributions, where $\sigma \in \mathbb{R}_{>0}$ , D is a diagonal matrix, and C is a positive definite full covariance matrix. Thin lines depict possible objective function contour lines
From (2) we naturally define the square root of C as
$$C^{\frac{1}{2}} = BDB^{\mathsf{T}} \tag{3}$$
and therefore
$$egin{array}{lcl} oldsymbol{C}^{- rac{1}{2}} &=& oldsymbol{B}oldsymbol{D}^{-1}oldsymbol{B}^{\mathsf{T}} \ &=& oldsymbol{B} \operatorname{diag}\left( rac{1}{d_1},\ldots, rac{1}{d_n} ight)oldsymbol{B}^{\mathsf{T}} \end{array}$$
0.2 The Multivariate Normal Distribution
A multivariate normal distribution, $\mathcal{N}(m,C)$ , has a unimodal, "bell-shaped" density, where the top of the bell (the modal value) corresponds to the distribution man, m. The distribution $\mathcal{N}(m,C)$ is uniquely determined by its mean $m \in \mathbb{R}^n$ and its symmetric and positive definite covariance matrix $C \in \mathbb{R}^{n \times n}$ . Covariance (positive definite) matrices have an appealing geometrical interpretation: they can be uniquely identified with the (hyper-)ellipsoid $\{x \in \mathbb{R}^n \mid x^T C^{-1}x = 1\}$ , as shown in Fig. 1. The ellipsoid is a surface of equal density of the distribution. The principal axes of the ellipsoid correspond to the eigenvectors of C, the squared axes lengths correspond to the eigenvalues. The eigendecomposition is denoted by $C = B(D)^2 B^T$ (see Sect. 0.1). If $D = \sigma I$ , where $\sigma \in \mathbb{R}_{>0}$ and I denotes the identity matrix, $C = \sigma^2 I$ and the ellipsoid is isotropic (Fig. 1, left). If B = I, then $C = D^2$ is a diagonal matrix and the ellipsoid is axis parallel oriented (middle). In the coordinate system given by the columns of B, the distribution $\mathcal{N}(0,C)$ is always uncorrelated.
The normal distribution N (m, C) can be written in different ways.
$$\mathcal{N}(\boldsymbol{m}, \boldsymbol{C}) \sim \boldsymbol{m} + \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \sim \boldsymbol{m} + \boldsymbol{C}^{\frac{1}{2}} \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \sim \boldsymbol{m} + \boldsymbol{B} \boldsymbol{D} \underbrace{\boldsymbol{B}^{\mathsf{T}} \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}_{\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})} \sim \boldsymbol{m} + \boldsymbol{B} \underbrace{\boldsymbol{D} \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}_{\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{D}^{2})}, \tag{4}$$
where "∼" denotes equality in distribution, and C 2 = BDBT. The last row can be well interpreted, from right to left
N (0, I) produces an spherical (isotropic) distribution as in Fig. 1, left.
D scales the spherical distribution within the coordinate axes as in Fig. 1, middle. DN (0, I) ∼ N 0, D^{2} has n independent components. The matrix D can be interpreted as (individual) step-size matrix and its diagonal entries are the standard deviations of the components.
B defines a new orientation for the ellipsoid, where the new principal axes of the ellipsoid correspond to the columns of B. Note that B has n 2−n 2 degrees of freedom.
Equation (4) is useful to compute N (m, C) distributed vectors, because N (0, I) is a vector of independent (0, 1)-normally distributed numbers that can easily be realized on a computer.
0.3 Randomized Black Box Optimization
We consider the black box search scenario, where we want to minimize an objective function (or cost function or fitness function)
$$f: \mathbb{R}^n \to \mathbb{R}$$ $x \mapsto f(x)$ .
The objective is to find one or more search points (candidate solutions), x ∈ R n, with a function value, f(x), as small as possible. We do not state the objective of searching for a global optimum, as this is often neither feasible nor relevant in practice. Black box optimization refers to the situation, where function values of evaluated search points are the only accessible information on f. 4 The search points to be evaluated can be freely chosen. We define the search costs as the number of executed function evaluations, in other words the amount of information we needed to acquire from f 5 . Any performance measure must consider the search costs together with the achieved objective function value.6
A randomized black box search algorithm is outlined in Fig. 2. In the CMA Evolution
4Knowledge about the underlying optimization problem might well enter the composition of f and the chosen problem encoding.
5Also f is sometimes denoted as cost function, but it should not to be confused with the search costs.
6A performance measure can be obtained from a number of trials as, for example, the mean number of function evaluations to reach a given function value, or the median best function value obtained after a given number of function evaluations.
Initialize distribution parameters \boldsymbol{\theta}^{(0)}
For generation g=0,1,2,\ldots
Sample \lambda independent points from distribution P\left(\boldsymbol{x}|\boldsymbol{\theta}^{(g)}\right) \rightarrow \boldsymbol{x}_1,\ldots,\boldsymbol{x}_{\lambda}
Evaluate the sample \boldsymbol{x}_1,\ldots,\boldsymbol{x}_{\lambda} on f
Update parameters \boldsymbol{\theta}^{(g+1)} = F_{\boldsymbol{\theta}}(\boldsymbol{\theta}^{(g)},(\boldsymbol{x}_1,f(\boldsymbol{x}_1)),\ldots,(\boldsymbol{x}_{\lambda},f(\boldsymbol{x}_{\lambda})))
break, if termination criterion met
Figure 2: Randomized black box search. $f: \mathbb{R}^n \to \mathbb{R}$ is the objective function
Strategy the search distribution, P, is a multivariate normal distribution. Given all variances and covariances, the normal distribution has the largest entropy of all distributions in $\mathbb{R}^n$ . Furthermore, coordinate directions are not distinguished in any way. Both makes the normal distribution a particularly attractive candidate for randomized search.
Randomized search algorithms are regarded to be robust in a rugged search landscape, which can comprise discontinuities, (sharp) ridges, or local optima. The covariance matrix adaptation (CMA) in particular is designed to tackle, additionally, ill-conditioned and non-separable problems.
0.4 Hessian and Covariance Matrices
We consider the convex-quadratic objective function $f_H: x \mapsto \frac{1}{2}x^\mathsf{T} H x$ , where the Hessian matrix $H \in \mathbb{R}^{n \times n}$ is a positive definite matrix. Given a search distribution $\mathcal{N}(m, C)$ , there is a close relation between H and C: Setting $C = H^{-1}$ on $f_H$ is equivalent to optimizing the isotropic function $f_{\mathrm{sphere}}(x) = \frac{1}{2}x^\mathsf{T}x = \frac{1}{2}\sum_i x_i^2$ (where $H = \mathbf{I}$ ) with $C = \mathbf{I}$ . That is, on convex-quadratic objective functions, setting the covariance matrix of the search distribution to the inverse Hessian matrix is equivalent to rescaling the ellipsoid function into a spherical one. Consequently, we assume that the optimal covariance matrix equals to the inverse Hessian matrix, up to a constant factor. Furthermore, choosing a covariance matrix or choosing a respective affine linear transformation of the search space (i.e. of x) is equivalent [14], because for any full rank $n \times n$ -matrix A we find a positive definite Hessian such that $\frac{1}{2}(Ax)^\mathsf{T}Ax = \frac{1}{2}x^\mathsf{T}A^\mathsf{T}Ax = \frac{1}{2}x^\mathsf{T}Hx$ .
The final objective of covariance matrix adaptation is to closely approximate the contour lines of the objective function f. On convex-quadratic functions this amounts to approximating the inverse Hessian matrix, similar to a quasi-Newton method.
In Fig. 1 the solid-line distribution in the right figure follows the objective function contours most suitably, and it is easy to foresee that it will aid to approach the optimum the most.
The condition number of a positive definite matrix $\boldsymbol{A}$ is defined via the Euclidean norm: $\operatorname{cond}(\boldsymbol{A}) \stackrel{\text{def}}{=} \|\boldsymbol{A}\| \times \|\boldsymbol{A}^{-1}\|$ , where $\|\boldsymbol{A}\| = \sup_{\|\boldsymbol{x}\|=1} \|\boldsymbol{A}\boldsymbol{x}\|$ . For a positive definite (Hessian or covariance) matrix $\boldsymbol{A}$ holds $\|\boldsymbol{A}\| = \lambda_{\max}$ and $\operatorname{cond}(\boldsymbol{A}) = \frac{\lambda_{\max}}{\lambda_{\min}} \geq 1$ , where $\lambda_{\max}$ and $\lambda_{\min}$ are the largest and smallest eigenvalue of $\boldsymbol{A}$ .
$<sup>^7</sup>$ An n-dimensional separable problem can be solved by solving n 1-dimensional problems separately, which is a far easier task.
<sup>8Also the initial mean value m has to be transformed accordingly.
<sup>9Even though there is good intuition and strong empirical evidence for this statement, a rigorous proof is missing.
1 Basic Equation: Sampling
In the CMA Evolution Strategy, a population of new search points (individuals, offspring) is generated by sampling a multivariate normal distribution.10 The basic equation for sampling the search points, for generation number g = 0, 1, 2, . . . , reads11
$$\boldsymbol{x}_{k}^{(g+1)} \sim \boldsymbol{m}^{(g)} + \sigma^{(g)} \mathcal{N} \left( \boldsymbol{0}, \boldsymbol{C}^{(g)} \right) \quad \text{for } k = 1, \dots, \lambda \tag{5} $$
where
∼ denotes the same distribution on the left and right side.
N(0, C(g) ) is a multivariate normal distribution with zero mean and covariance matrix C(g) , see Sect. 0.2. It holds m(g) + σ (g)N(0, C(g) ) ∼ N m(g) ,(σ (g) ) 2C(g) .
x (g+1) k ∈ R n, k-th offspring (individual, search point) from generation g + 1.
m(g) ∈ R n, mean value of the search distribution at generation g.
σ (g) ∈ R>0, "overall" standard deviation, step-size, at generation g.
C(g) ∈ R n×n, covariance matrix at generation g. Up to the scalar factor σ (g) 2 , C(g) is the covariance matrix of the search distribution.
λ ≥ 2, population size, sample size, number of offspring.
To define the complete iteration step, the remaining question is, how to calculate m(g+1) , C(g+1), and σ (g+1) for the next generation g + 1. The next three sections will answer these questions, respectively. An algorithm summary with all parameter settings and MAT-LAB source code are given in Appendix A and C, respectively.
2 Selection and Recombination: Moving the Mean
The new mean m(g+1) of the search distribution is a weighted average of µ selected points from the sample x (g+1) 1 , . . . , x (g+1) λ :
$$\mathbf{m}^{(g+1)} = \sum_{i=1}^{\mu} w_i \, \mathbf{x}_{i:\lambda}^{(g+1)} \tag{6} $$
$$\sum_{i=1}^{\mu} w_i = 1, \qquad w_1 \ge w_2 \ge \dots \ge w_{\mu} > 0 \tag{7}$$
where
10Recall that, given all (co-)variances, the normal distribution has the largest entropy of all distributions in Rn.
11Framed equations belong to the final algorithm of a CMA Evolution Strategy.
$\mu \leq \lambda$ is the parent population size, i.e. the number of selected points.
$w_{i=1...\mu} \in \mathbb{R}_{>0}$ , positive weight coefficients for recombination. For $w_{i=1...\mu} = 1/\mu$ , Equation (6) calculates the mean value of $\mu$ selected points.
$m{x}_{i:\lambda}^{(g+1)}, i$ -th best individual out of $m{x}_1^{(g+1)}, \dots, m{x}_{\lambda}^{(g+1)}$ from (5). The index $i:\lambda$ denotes the index of the i-th ranked individual and $f(m{x}_{1:\lambda}^{(g+1)}) \leq f(m{x}_{2:\lambda}^{(g+1)}) \leq \dots \leq f(m{x}_{\lambda:\lambda}^{(g+1)}),$ where f is the objective function to be minimized.
Equation (6) implements truncation selection by choosing $\mu < \lambda$ out of $\lambda$ offspring points. Assigning different weights $w_i$ should also be interpreted as a selection mechanism. Equation (6) implements weighted intermediate recombination by taking $\mu > 1$ individuals into account for a weighted average.
The measure^{12}
$$\mu_{\text{eff}} = \left(\frac{\|\boldsymbol{w}\|_{1}}{\|\boldsymbol{w}\|_{2}}\right)^{2} = \frac{\|\boldsymbol{w}\|_{1}^{2}}{\|\boldsymbol{w}\|_{2}^{2}} = \frac{\left(\sum_{i=1}^{\mu} |w_{i}|\right)^{2}}{\sum_{i=1}^{\mu} w_{i}^{2}} = \frac{1}{\sum_{i=1}^{\mu} w_{i}^{2}} \tag{8} $$
will be repeatedly used in the following and can be paraphrased as effective sample size of the selected samples or variance effective selection mass. From the definition of $w_i$ in (7) we derive $1 \le \mu_{\text{eff}} \le \mu$ , and $\mu_{\text{eff}} = \mu$ for equal recombination weights, i.e. $w_i = 1/\mu$ for all $i=1\ldots\mu$ .
The notion of $\mu_{\text{eff}}$ with different recombination weights generalizes the notion of $\mu$ with equal recombination weights in several aspects. The number $\mu$ (with equal recombination weights) is the amount of information used, expressed as number of independent sources. Taking the weighted average of independent samples reduces the original variance by a factor of $\mu$ for equal weights and by a factor of $\mu_{\rm eff}$ for any weights, hence $\mu_{\rm eff}$ can be considered as the amount of used information. To keep the variance unchanged, the average must be multiplied by $\sqrt{\mu_{\rm eff}}$ . However, the optimal step-size (given $\mu < n$ ) is proportional to $\mu$ [6, 33] for equal weights and proportional to 1.25 $\mu_{\rm eff}$ for optimal recombination weights [4], respectively, see also Section 4.
Usually, $\mu_{\rm eff} \approx \lambda/4$ indicates a reasonable setting of $w_i$ . A simple and reasonable setting is $w_i \propto \mu - i + 1$ , and $\mu \approx \lambda/2$ , where $\mu_{\text{eff}} \approx 3\lambda/8$ .
The final equation rewrites (6) as an update of m,
$$m^{(g+1)} = m^{(g)} + c_{\text{m}} \sum_{i=1}^{\mu} w_i \left( x_{i:\lambda}^{(g+1)} - m^{(g)} \right) \tag{9} $$
where
$c_{\rm m}$ is a learning rate, usually set to 1.13
Equation (9) generalizes (6). If $c_m \sum_{i=1}^{\mu} w_i = 1$ , as it is the case with the default parameter setting (compare Table 1 in Appendix A), $-m^{(g)}$ cancels out $m^{(g)}$ , and Equations (9) and (6) are identical.
<sup>12Later, the vector w will have $\lambda \geq \mu$ elements. Here, for computing the norm, we assume that any additional $\lambda-\mu$ elements are zero. 13In the literature the notation $\kappa=1/c_{\rm m}$ is also common and $\kappa$ is used as multiplier in (5) instead of in (9).
Choosing c^{m} < 1 can be advantageous on noisy functions. With optimal step-size we have roughly σ ∝ 1/cm, hence the "test steps" in (5) are in effect increased whereas the update step in (9) remains unchanged. However, too large test steps negatively impact the performance because the ranking indices i : λ are determined too far away from the (current) region of relevance. Arbitrary small test steps (when c^{m} → ∞) work generally well, within the limits of numerical precision, on unimodal and noisefree functions [1, 11].
3 Adapting the Covariance Matrix
In this section, the update of the covariance matrix, C, is derived. We will start out estimating the covariance matrix from a single population of one generation (Sect. 3.1). For small populations this estimation is unreliable and an adaptation procedure has to be invented (rank-µupdate, Sect. 3.2). In the limit case only a single point can be used to update (adapt) the covariance matrix at each generation (rank-one-update, Sect. 3.3). This adaptation can be enhanced by exploiting dependencies between successive steps applying cumulation (Sect. 3.3.2). Finally we combine the rank-µ and rank-one updating methods (Sect. 3.4).
3.1 Estimating the Covariance Matrix From Scratch
For the moment we assume that the population contains enough information to reliably estimate a covariance matrix from the population.14 For the sake of convenience we assume σ (g) = 1 (see (5)) in this section. For σ (g) 6= 1 the formulae hold except for a constant factor. We can (re-)estimate the original covariance matrix C(g) using the sampled population from (5), x (g+1) 1 . . . x (g+1) λ , via the empirical covariance matrix
$$C_{\text{emp}}^{(g+1)} = \frac{1}{\lambda - 1} \sum_{i=1}^{\lambda} \left( \boldsymbol{x}_{i}^{(g+1)} - \frac{1}{\lambda} \sum_{j=1}^{\lambda} \boldsymbol{x}_{j}^{(g+1)} \right) \left( \boldsymbol{x}_{i}^{(g+1)} - \frac{1}{\lambda} \sum_{j=1}^{\lambda} \boldsymbol{x}_{j}^{(g+1)} \right)^{\mathsf{T}} . \tag{10}$$
The empirical covariance matrix C (g+1) emp is an unbiased estimator of C(g) : assuming the x (g+1) i , i = 1 . . . λ, to be random variables (rather than a realized sample), we have that E -C (g+1) emp C(g) = C(g) . Consider now a slightly different approach to get an estimator for C(g) .
$$\boldsymbol{C}_{\lambda}^{(g+1)} = \frac{1}{\lambda} \sum_{i=1}^{\lambda} \left( \boldsymbol{x}_{i}^{(g+1)} - \boldsymbol{m}^{(g)} \right) \left( \boldsymbol{x}_{i}^{(g+1)} - \boldsymbol{m}^{(g)} \right)^{\mathsf{T}} \tag{11} $$
Also the matrix C (g+1) λ is an unbiased estimator of C(g) . The remarkable difference between (10) and (11) is the reference mean value. For C (g+1) emp it is the mean of the actually realized sample. For C (g+1) λ it is the true mean value, m(g) , of the sampled distribution (see (5)). Therefore, the estimators C (g+1) emp and C (g+1) λ can be interpreted differently: while C (g+1) emp
14To re-estimate the covariance matrix, C, from a N (0, I) distributed sample such that cond(C) < 10 a sample size λ ≥ 4n is needed, as can be observed in numerical experiments.
estimates the distribution variance within the sampled points, $C_{\lambda}^{(g+1)}$ estimates variances of sampled steps, $x_i^{(g+1)} - m^{(g)}$ .
A minor difference between (10) and (11) is the different normalizations $\frac{1}{\lambda-1}$ versus $\frac{1}{\lambda}$ , necessary to get an unbiased estimator in both cases. In (10) one degree of freedom is already taken by the inner summand. In order to get a maximum likelihood estimator, in both cases $\frac{1}{\lambda}$ must be used.
Equation (11) re-estimates the original covariance matrix. To "estimate" a "better" covariance matrix, the same, weighted selection mechanism as in (6) is used [21].
$$C_{\mu}^{(g+1)} = \sum_{i=1}^{\mu} w_i \left( x_{i:\lambda}^{(g+1)} - m^{(g)} \right) \left( x_{i:\lambda}^{(g+1)} - m^{(g)} \right)^{\mathsf{T}} \tag{12} $$
The matrix $C_{\mu}^{(g+1)}$ is an estimator for the distribution of selected steps, just as $C_{\lambda}^{(g+1)}$ is an estimator of the original distribution of steps before selection. Sampling from $C_{\mu}^{(g+1)}$ tends to reproduce selected, i.e. successful steps, giving a justification for what a "better" covariance matrix means.
Following [15], we compare (12) with the Estimation of Multivariate Normal Algorithm $EMNA_{global}$ [30, 31]. The covariance matrix in $EMNA_{global}$ reads, similar to (10),
$$C_{\text{EMNA}_{global}}^{(g+1)} = \frac{1}{\mu} \sum_{i=1}^{\mu} \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g+1)} \right) \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g+1)} \right)^{\mathsf{T}} , \quad (13)$$
where $\boldsymbol{m}^{(g+1)} = \frac{1}{\mu} \sum_{i=1}^{\mu} \boldsymbol{x}_{i:\lambda}^{(g+1)}$ . Similarly, applying the so-called Cross-Entropy method to continuous domain optimization [34] yields the covariance matrix $\frac{\mu}{\mu-1} \boldsymbol{C}_{\mathrm{EMNA}_{global}}^{(g+1)}$ , i.e. the unbiased empirical covariance matrix of the $\mu$ best points. In both cases the subtle, but most important difference to (12) is, again, the choice of the reference mean value. Equation (13) estimates the variance within the selected population while (12) estimates selected steps. Equation (13) reveals always smaller variances than (12), because its reference mean value is the minimizer for the variances. Moreover, in most conceivable selection situations (13) decreases the variances compared to $\boldsymbol{C}^{(g)}$ .
Figure 3 demonstrates the estimation results on a linear objective function for $\lambda=150$ , $\mu=50$ , and $w_i=1/\mu$ . Equation (12) geometrically increases the expected variance in direction of the gradient (where the selection takes place, here the diagonal), given ordinary settings for parent number $\mu$ and recombination weights $w_1,\ldots,w_\mu$ . Equation (13) always decreases the variance in gradient direction geometrically fast! Therefore, (13) is highly susceptible to premature convergence, in particular with small parent populations, where the population cannot be expected to bracket the optimum at any time. However, for large values of $\mu$ in large populations with large initial variances, the impact of the different reference mean value can become marginal.
In order to ensure with (5), (6), and (12), that $C_{\mu}^{(g+1)}$ is a reliable estimator, the variance effective selection mass $\mu_{\rm eff}$ (cf. (8)) must be large enough: getting condition numbers (cf. Sect. 0.4) smaller than ten for $C_{\mu}^{(g)}$ on $f_{\rm sphere}(\boldsymbol{x}) = \sum_{i=1}^n x_i^2$ , requires $\mu_{\rm eff} \approx 10n$ . The next step is to circumvent this restriction on $\mu_{\rm eff}$ .
15 Taking a weighted sum, $\sum_{i=1}^{\mu} w_i \dots$ , instead of the mean, $\frac{1}{\mu} \sum_{i=1}^{\mu} \dots$ , is an appealing, but less important, difference
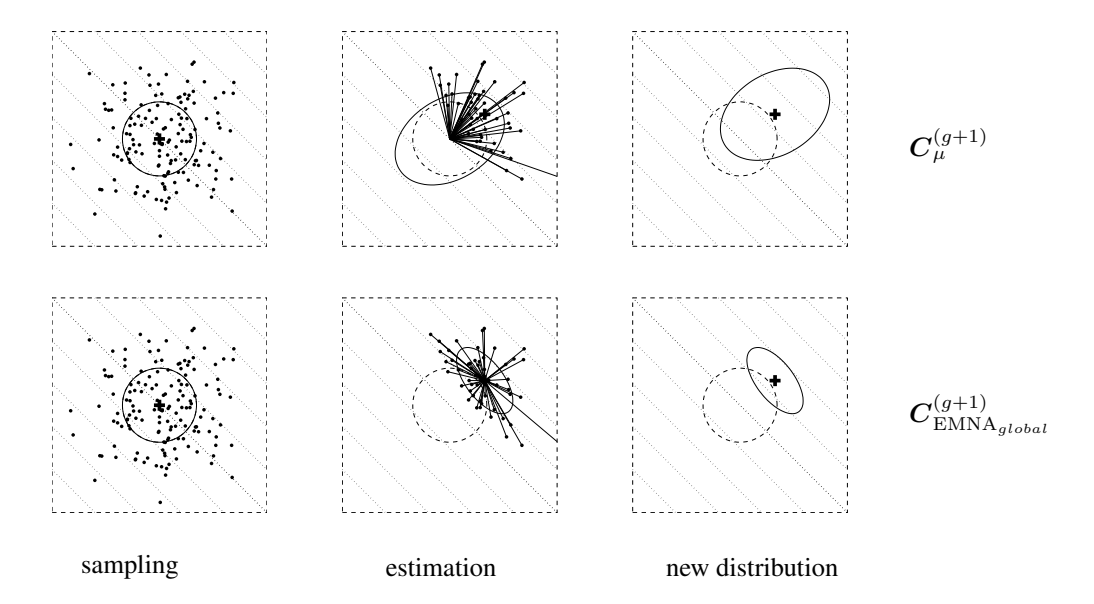
Figure 3: Estimation of the covariance matrix on $f_{\text{linear}}(\boldsymbol{x}) = -\sum_{i=1}^2 x_i$ to be minimized. Contour lines (dotted) indicate that the strategy should move toward the upper right corner. Above: estimation of $\boldsymbol{C}_{\mu}^{(g+1)}$ according to (12), where $w_i = 1/\mu$ . Below: estimation of $\boldsymbol{C}_{\text{EMNA}_{global}}^{(g+1)}$ according to (13). Left: sample of $\lambda = 150 \ \mathcal{N}(\mathbf{0}, \mathbf{I})$ distributed points. Middle: the $\mu = 50$ selected points (dots) determining the entries for the estimation equation (solid straight lines). Right: search distribution of the next generation (solid ellipsoids). Given $w_i = 1/\mu$ , estimation via $\boldsymbol{C}_{\mu}^{(g+1)}$ increases the expected variance in gradient direction for all $\mu < \lambda/2$ , while estimation via $\boldsymbol{C}_{\text{EMNA}_{global}}^{(g+1)}$ decreases this variance for any $\mu < \lambda$ geometrically fast
3.2 Rank- $\mu$ -Update
To achieve fast search (opposite to more robust or more global search), e.g. competitive performance on $f_{\rm sphere}: \boldsymbol{x} \mapsto \sum x_i^2$ , the population size $\lambda$ must be small. Because typically (and ideally) $\mu_{\rm eff} \approx \lambda/4$ also $\mu_{\rm eff}$ must be small and we may assume, e.g., $\mu_{\rm eff} \leq 1 + \ln n$ . Then, it is not possible to get a reliable estimator for a good covariance matrix from (12). As a remedy, information from previous generations is used additionally. For example, after a sufficient number of generations, the mean of the estimated covariance matrices from all generations,
$$C^{(g+1)} = \frac{1}{g+1} \sum_{i=0}^{g} \frac{1}{\sigma^{(i)^2}} C_{\mu}^{(i+1)} \tag{14} $$
becomes a reliable estimator for the selected steps. To make $C_{\mu}^{(g)}$ from different generations comparable, the different $\sigma^{(i)}$ are incorporated. (Assuming $\sigma^{(i)} = 1$ , (14) resembles the covariance matrix from the Estimation of Multivariate Normal Algorithm EMNA_{i} [31].)
In (14), all generation steps have the same weight. To assign recent generations a higher
weight, exponential smoothing is introduced. Choosing $C^{(0)} = \mathbf{I}$ to be the unity matrix and a learning rate $0 < c_u \le 1$ , then $C^{(g+1)}$ reads
$$C^{(g+1)} = (1 - c_{\mu})C^{(g)} + c_{\mu} \frac{1}{\sigma^{(g)^{2}}} C_{\mu}^{(g+1)}$$
$$= (1 - c_{\mu})C^{(g)} + c_{\mu} \sum_{i=1}^{\mu} w_{i} \mathbf{y}_{i:\lambda}^{(g+1)} \mathbf{y}_{i:\lambda}^{(g+1)^{\mathsf{T}}}, \qquad (15)$$
where
$c_{\mu} \leq 1$ learning rate for updating the covariance matrix. For $c_{\mu} = 1$ , no prior information is retained and $C^{(g+1)} = \frac{1}{\sigma^{(g)^2}} C_{\mu}^{(g+1)}$ . For $c_{\mu} = 0$ , no learning takes place and $C^{(g+1)} = C^{(0)}$ . Here, $c_{\mu} \approx \min(1, \mu_{\text{eff}}/n^2)$ is a reasonably choice.
$w_{1...\mu} \in \mathbb{R}$ such that $w_1 \geq \cdots \geq w_{\mu} > 0$ and $\sum_i w_i = 1$ .
$$y_{i\cdot\lambda}^{(g+1)} = (x_{i\cdot\lambda}^{(g+1)} - m^{(g)})/\sigma^{(g)}.$$
$oldsymbol{z}_{i:\lambda}^{(g+1)} = oldsymbol{C}^{(g)} oldsymbol{y}_{i:\lambda}^{(g+1)}$ is the mutation vector expressed in the unique coordinate system where the sampling is isotropic and the respective coordinate system transformation does not rotate the original principal axes of the distribution.
This covariance matrix update is called rank- $\mu$ -update [23], because the sum of outer products in (15) is of rank $\min(\mu, n)$ with probability one (given $\mu$ non-zero weights). This sum can even consist of a single term, if $\mu = 1$ .
Finally, we generalize (15) to $\lambda$ weight values which need neither sum to 1, nor be non-negative anymore [28, 27],
$$\boldsymbol{C}^{(g+1)} = (1 - c_{\mu} \sum w_{i}) \boldsymbol{C}^{(g)} + c_{\mu} \sum_{i=1}^{\lambda} w_{i} \boldsymbol{y}_{i:\lambda}^{(g+1)} \boldsymbol{y}_{i:\lambda}^{(g+1)^{\mathsf{T}}}$$
$$= \boldsymbol{C}^{(g)^{1/2}} \left( \mathbf{I} + c_{\mu} \sum_{i=1}^{\lambda} w_{i} \left( \boldsymbol{z}_{i:\lambda}^{(g+1)} \boldsymbol{z}_{i:\lambda}^{(g+1)^{\mathsf{T}}} - \mathbf{I} \right) \right) \boldsymbol{C}^{(g)^{1/2}} , \tag{16} $$
where
$w_{1...\lambda} \in \mathbb{R}$ such that $w_1 \geq \cdots \geq w_{\mu} > 0 \geq w_{\mu+1} \geq w_{\lambda}$ , and usually $\sum_{i=1}^{\mu} w_i = 1$ and $\sum_{i=1}^{\lambda} w_i \approx 0$ .
$$\sum w_i = \sum_{i=1}^{\lambda} w_i$$
The second line of (16) expresses the update in the natural coordinate system, an idea already considered in [12]. The identity covariance matrix is updated and a coordinate system transformation is applied afterwards by multiplication with $C^{(g)^{1/2}}$ on both sides. Equation (16) uses $\lambda$ weights, $w_i$ , of which about half are negative. If the weights are chosen such that $\sum w_i = 0$ , the decay on $C^{(g)}$ disappears and changes are only made along axes in which samples are realized.
Negative values for the recombination weights in the covariance matrix update have been introduced in the seminal paper of Jastrebski and Arnold [28] as active covariance matrix adaptation. Non-equal negative weight values have been used in [27] together with a rather involved mechanism to make up for different vector lengths. The default recombination weights as defined in Table 1 in Appendix A are somewhere in between these two proposals, but closer to [28]. Slightly deviating from (16) later on, vector lengths associated with negative weights will be rescaled to a (direction dependent) constant, see (46) and (47) in Appendix A. This allows to guaranty positive definiteness of $C^{(g+1)}$ . Conveniently, it also alleviates a selection error which usually makes directions associated with longer vectors
The number $1/c_{\mu}$ is the backward time horizon that contributes roughly 63% of the overall information.
Because (16) expands to the weighted sum
$$\boldsymbol{C}^{(g+1)} = (1 - c_{\mu})^{g+1} \boldsymbol{C}^{(0)} + c_{\mu} \sum_{i=0}^{g} (1 - c_{\mu})^{g-i} \frac{1}{\sigma^{(i)}} \boldsymbol{C}_{\mu}^{(i+1)} , \qquad (17)$$
the backward time horizon, $\Delta g$ , where about 63% of the overall weight is summed up, is defined by
$$c_{\mu} \sum_{i=a+1-\Delta a}^{g} (1 - c_{\mu})^{g-i} \approx 0.63 \approx 1 - \frac{1}{e} \tag{18} $$
Resolving the sum yields
$$(1 - c_{\mu})^{\Delta g} \approx \frac{1}{e} , \qquad (19)$$
and resolving for $\Delta g$ , using the Taylor approximation for ln, yields
$$\Delta g \approx \frac{1}{c_{\mu}} \tag{20} $$
That is, approximately 37% of the information in $C^{(g+1)}$ is older than $1/c_{\mu}$ generations, and, according to (19), the original weight is reduced by a factor of 0.37 after approximately $1/c_{\mu}$ generations. 16
The choice of $c_{\mu}$ is crucial. Small values lead to slow learning, too large values lead to a failure, because the covariance matrix degenerates. Fortunately, a good setting seems to be largely independent of the function to be optimized.17 A first order approximation for a good choice is $c_{\mu} \approx \mu_{\rm eff}/n^2$ . Therefore, the characteristic time horizon for (16) is roughly $n^2/\mu_{\rm eff}$ .
Experiments suggest that $c_{\mu} \approx \mu_{\rm eff}/n^2$ is a rather conservative setting for large values of n, whereas $\mu_{\rm eff}/n^{1.5}$ appears to be slightly beyond the limit of stability. The best, yet robust choice of the exponent remains to be an open question.
Even for the learning rate $c_{\mu} = 1$ , adapting the covariance matrix cannot be accomplished within one generation. The effect of the original sample distribution does not vanish until a sufficient number of generations. Assuming fixed search costs (number of function evaluations), a small population size $\lambda$ allows a larger number of generations and therefore usually leads to a faster adaptation of the covariance matrix.
This can be shown more easily, because $(1-c_{\mu})^g=\exp\ln(1-c_{\mu})^g=\exp(g\ln(1-c_{\mu}))\approx\exp(-gc_{\mu})$ for small $c_{\mu}$ , and for $g\approx 1/c_{\mu}$ we get immediately $(1-c_{\mu})^g\approx\exp(-1)$ .
17 We use the sphere model $f_{\rm sphere}(\boldsymbol{x})=\sum_i x_i^2$ to empirically find a good setting for the parameter $c_{\mu}$ , dependent
on n and $\mu_{\rm eff}$ . The found setting was applicable to any non-noisy objective function we tried so far.
3.3 Rank-One-Update
In Section 3.1 we started by estimating the complete covariance matrix from scratch, using all selected steps from a single generation. We now take an opposite viewpoint. We repeatedly update the covariance matrix in the generation sequence using a single selected step only. First, this perspective will give another justification of the adaptation rule (16). Second, we will introduce the so-called evolution path that is finally used for a rank-one update of the covariance matrix.
3.3.1 A Different Viewpoint
We consider a specific method to produce n-dimensional normal distributions with zero mean. Let the vectors $\mathbf{y}_1, \dots, \mathbf{y}_{g_0} \in \mathbb{R}^n$ , $g_0 \geq n$ , span $\mathbb{R}^n$ and let $\mathcal{N}(0,1)$ denote independent (0,1)-normally distributed random numbers, then
$$\mathcal{N}(0,1) \boldsymbol{y}_1 + \dots + \mathcal{N}(0,1) \boldsymbol{y}_{g_0} \sim \mathcal{N}\left(\boldsymbol{0}, \sum_{i=1}^{g_0} \boldsymbol{y}_i \boldsymbol{y}_i^\mathsf{T}\right) \tag{21} $$
is a normally distributed random vector with zero mean and covariance matrix $\sum_{i=1}^{g_0} \boldsymbol{y}_i \boldsymbol{y}_i^\mathsf{T}$ . The random vector (21) is generated by adding "line-distributions" $\mathcal{N}(0,1) \boldsymbol{y}_i$ . The singular distribution $\mathcal{N}(0,1) \boldsymbol{y}_i \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{y}_i \boldsymbol{y}_i^\mathsf{T})$ generates the vector $\boldsymbol{y}_i$ with maximum likelihood considering all normal distributions with zero mean.
The line distribution that generates a vector $\boldsymbol{y}$ with the maximum likelihood must "live" on a line that includes $\boldsymbol{y}$ , and therefore the distribution must obey $\mathcal{N}(0,1)\sigma\boldsymbol{y}\sim\mathcal{N}(0,\sigma^2\boldsymbol{y}\boldsymbol{y}^{\mathsf{T}})$ . Any other line distribution with zero mean cannot generate $\boldsymbol{y}$ at all. Choosing $\sigma$ reduces to choosing the maximum likelihood of $\|\boldsymbol{y}\|$ for the one-dimensional gaussian $\mathcal{N}(0,\sigma^2\|\boldsymbol{y}\|^2)$ , which is $\sigma=1$ .
The covariance matrix $yy^T$ has rank one, its only eigenvectors are $\{\alpha y \mid \alpha \in \mathbb{R}_{\setminus 0}\}$ with eigenvalue $\|y\|^2$ . Using equation (21), any normal distribution can be realized if $y_i$ are chosen appropriately. For example, (21) resembles (4) with m=0, using the orthogonal eigenvectors $y_i=d_{ii}b_i$ , for $i=1,\ldots,n$ , where $b_i$ are the columns of B. In general, the vectors $y_i$ need not to be eigenvectors of the covariance matrix, and they usually are not.
Considering (21) and a slight simplification of (16), we try to gain insight into the adaptation rule for the covariance matrix. Let the sum in (16) consist of a single summand only (e.g. $\mu=1$ ), and let $y_{g+1}=\frac{\boldsymbol{x}_{1:\lambda}^{(g+1)}-\boldsymbol{m}^{(g)}}{\sigma^{(g)}}$ . Then, the rank-one update for the covariance matrix reads
$$C^{(g+1)} = (1-c_1)C^{(g)} + c_1 y_{g+1}y_{g+1}^{\mathsf{T}} \tag{22} $$
The right summand is of rank one and adds the maximum likelihood term for $y_{g+1}$ into the covariance matrix $C^{(g)}$ . Therefore the probability to generate $y_{g+1}$ in the next generation increases.
An example of the first two iteration steps of (22) is shown in Figure 4. The distribution $\mathcal{N}(\mathbf{0}, \mathbf{C}^{(1)})$ tends to reproduce $\mathbf{y}_1$ with a larger probability than the initial distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$ ; the distribution $\mathcal{N}(\mathbf{0}, \mathbf{C}^{(2)})$ tends to reproduce $\mathbf{y}_2$ with a larger probability than $\mathcal{N}(\mathbf{0}, \mathbf{C}^{(1)})$ , and so forth. When $\mathbf{y}_1, \ldots, \mathbf{y}_g$ denote the formerly selected, favorable steps, $\mathcal{N}(\mathbf{0}, \mathbf{C}^{(g)})$
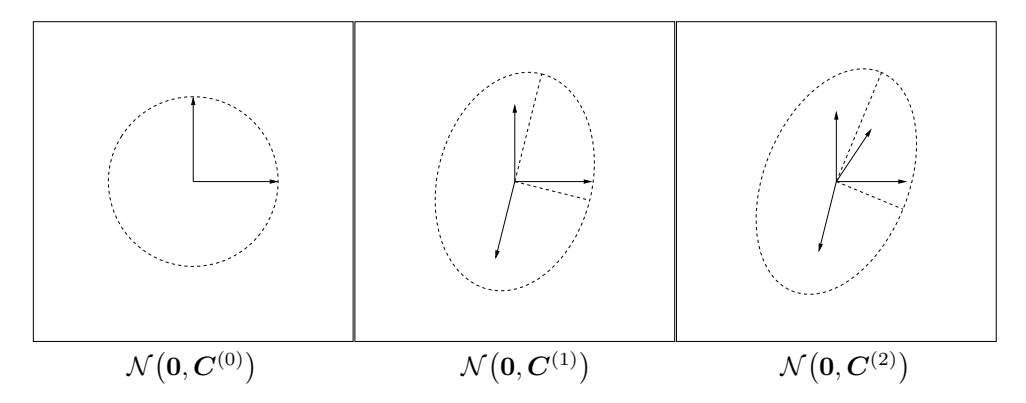
Figure 4: Change of the distribution according to the covariance matrix update (22). Left: vectors $e_1$ and $e_2$ , and $C^{(0)} = \mathbf{I} = e_1 e_1^\mathsf{T} + e_2 e_2^\mathsf{T}$ . Middle: vectors $0.91 \, e_1$ , $0.91 \, e_2$ , and $0.41 \, y_1$ (the coefficients deduce from $c_1 = 0.17$ ), and $C^{(1)} = (1 - c_1) \, \mathbf{I} + c_1 \, y_1 y_1^\mathsf{T}$ , where $y_1 = \begin{pmatrix} -0.59 \\ -2.2 \end{pmatrix}$ . The distribution ellipsoid is elongated into the direction of $y_1$ , and therefore increases the likelihood of $y_1$ . Right: $C^{(2)} = (1 - c_1) \, C^{(1)} + c_1 \, y_2 y_2^\mathsf{T}$ , where $y_2 = \begin{pmatrix} 0.97 \\ 1.5 \end{pmatrix}$ .
tends to reproduce these steps. The process leads to an alignment of the search distribution $\mathcal{N}(\mathbf{0}, \mathbf{C}^{(g)})$ to the distribution of the selected steps. If both distributions become alike, as under random selection, in expectation no further change of the covariance matrix takes place [13].
3.3.2 Cumulation: Utilizing the Evolution Path
We have used the selected steps, $\boldsymbol{y}_{i:\lambda}^{(g+1)} = (\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)})/\sigma^{(g)}$ , to update the covariance matrix in (16) and (22). Because $\boldsymbol{y}\boldsymbol{y}^{\mathsf{T}} = -\boldsymbol{y}(-\boldsymbol{y})^{\mathsf{T}}$ , the sign of the steps is irrelevant for the update of the covariance matrix—that is, the sign information is lost when calculating $\boldsymbol{C}^{(g+1)}$ . To reintroduce the sign information, a so-called evolution path is constructed [24, 26].
We call a sequence of successive steps, the strategy takes over a number of generations, an evolution path. An evolution path can be expressed by a sum of consecutive steps. This summation is referred to as cumulation. To construct an evolution path, the step-size $\sigma$ is disregarded. For example, an evolution path of three steps of the distribution mean m can be constructed by the sum
$$\frac{\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}}{\sigma^{(g)}} + \frac{\boldsymbol{m}^{(g)} - \boldsymbol{m}^{(g-1)}}{\sigma^{(g-1)}} + \frac{\boldsymbol{m}^{(g-1)} - \boldsymbol{m}^{(g-2)}}{\sigma^{(g-2)}} . \tag{23}$$
In practice, to construct the evolution path, $p_c \in \mathbb{R}^n$ , we use exponential smoothing as in (16), and start with $p_c^{(0)} = 0$ .18
$$p_{c}^{(g+1)} = (1 - c_{c})p_{c}^{(g)} + \sqrt{c_{c}(2 - c_{c})\mu_{eff}} \frac{\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}}{c_{m}\sigma^{(g)}} \tag{24} $$
where
<sup>18In the final algorithm (24) is still slightly modified, compare (45).
$p_{c}^{(g)} \in \mathbb{R}^{n}$ , evolution path at generation g.
$c_{\rm c} \leq 1$ . Again, $1/c_{\rm c}$ is the backward time horizon of the evolution path $p_{\rm c}$ that contains roughly 63% of the overall weight (compare derivation of (20)). A time horizon between $\sqrt{n}$ and n is effective.
The factor $\sqrt{c_{\rm c}(2-c_{\rm c})\mu_{\rm eff}}$ is a normalization constant for $\boldsymbol{p}_{\rm c}$ . For $c_{\rm c}=1$ and $\mu_{\rm eff}=1$ , the factor reduces to one, and $\boldsymbol{p}_{\rm c}^{(g+1)}=(\boldsymbol{x}_{1\cdot\lambda}^{(g+1)}-\boldsymbol{m}^{(g)})/\sigma^{(g)}$ .
The factor $\sqrt{c_{\mathrm{c}}(2-c_{\mathrm{c}})\mu_{\mathrm{eff}}}$ is chosen, such that
$$\boldsymbol{p}_c^{(g+1)} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \tag{25}$$
if
$$p_{c}^{(g)} \sim \frac{\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)}}{\sigma^{(g)}} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \quad \text{for all } i = 1, \dots, \mu \quad . \tag{26} $$
To derive (25) from (26) and (24) remark that
$$(1 - c_{\rm c})^2 + \sqrt{c_{\rm c}(2 - c_{\rm c})}^2 = 1$$ and $\sum_{i=1}^{\mu} w_i \mathcal{N}_i(\mathbf{0}, \mathbf{C}) \sim \frac{1}{\sqrt{\mu_{\rm eff}}} \mathcal{N}(\mathbf{0}, \mathbf{C})$ (27)
The (rank-one) update of the covariance matrix $C^{(g)}$ via the evolution path $p_c^{(g+1)}$ reads [24]
$$C^{(g+1)} = (1 - c_1)C^{(g)} + c_1 p_c^{(g+1)} p_c^{(g+1)^{\mathsf{T}}}. \tag{28} $$
An empirically validated choice for the learning rate in (28) is $c_1 \approx 2/n^2$ . For $c_c = 1$ and $\mu = 1$ , Equations (28), (22), and (16) are identical.
Using the evolution path for the update of C is a significant improvement of (16) for small $\mu_{\rm eff}$ , because correlations between consecutive steps are heavily exploited. The leading signs of steps, and the dependencies between consecutive steps play a significant role for the resulting evolution path $p_{\rm c}^{(g+1)}$ .
We consider the two most extreme situations, fully correlated steps and entirely anticorrelated steps. The summation in (24) reads for positive correlations
$$\sum_{i=0}^{g} (1 - c_{\rm c})^i \to \frac{1}{c_{\rm c}} \quad (\text{for } g \to \infty) \ ,$$
and for negative correlations
$$\sum_{i=0}^{g} (-1)^{i} (1 - c_{c})^{i} = \sum_{i=0}^{\lfloor g/2 \rfloor} (1 - c_{c})^{2i} - \sum_{i=0}^{(g-1)/2} (1 - c_{c})^{2i+1}$$
$$= \sum_{i=0}^{\lfloor g/2 \rfloor} (1 - c_{c})^{2i} - (1 - c_{c}) \sum_{i=0}^{(g-1)/2} (1 - c_{c})^{2i}$$
$$= c_{c} \sum_{i=0}^{\lfloor g/2 \rfloor} \left( (1 - c_{c})^{2} \right)^{i} + (1 - c_{c})^{g} ((g+1) \mod 2)$$
$$\rightarrow \frac{c_{c}}{1 - (1 - c_{c})^{2}} = \frac{1}{2 - c_{c}} \quad (\text{for } g \to \infty) .$$
Multipling these by $\sqrt{c_c(2-c_c)}$ , which is applied to each input vector, we find that the length of the evolution path is modulated by the factor of up to
$$\sqrt{\frac{2 - c_{\rm c}}{c_{\rm c}}} \approx \frac{1}{\sqrt{c_{\rm c}}} \tag{29}$$
due to the positive correlations, or its inverse due to negative correlations, respectively [19, Equations (48) and (49)].
With $\sqrt{n} \le 1/c_c \le n/2$ the number of function evaluations needed to adapt a nearly optimal covariance matrix on cigar-like objective functions becomes $\mathcal{O}(n)$ , despite a learning rate of $c_1 \approx 2/n^2$ [19]. A plausible interpretation of this effect is two-fold. First, the desired axis is represented in the path (much) more accurately than in single steps. Second, the learning rate $c_1$ is modulated: the increased length of the evolution path as computed in (29) acts in effect similar to an increased learning rate by a factor of up to $c_c^{-1/2}$ .
As a last step, we combine (16) and (28).
3.4 Combining Rank- $\mu$ -Update and Cumulation
The final CMA update of the covariance matrix combines (16) and (28).
$$C^{(g+1)} = \underbrace{(1 - c_1 - c_\mu \sum w_j)}_{\text{can be close or equal to 0}} C^{(g)}$$
$$+ c_1 \underbrace{\boldsymbol{p}_{c}^{(g+1)} \boldsymbol{p}_{c}^{(g+1)}}_{\text{rank-one update}}^{T} + c_\mu \underbrace{\sum_{i=1}^{\lambda} w_i \, \boldsymbol{y}_{i:\lambda}^{(g+1)} \left(\boldsymbol{y}_{i:\lambda}^{(g+1)}\right)}_{\text{rank-}\mu \text{ update}}^{T} \tag{30} $$
where
$$c_1 \approx 2/n^2$$ . $$c_\mu \approx \min(\mu_{\mathrm{eff}}/n^2, 1 - c_1).$$
$$\boldsymbol{y}_{i:\lambda}^{(g+1)} = (\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)})/\sigma^{(g)}.$$
$$\sum w_j = \sum_{i=1}^{\lambda} w_i \approx -c_1/c_\mu, \text{ but see also (53) and(46) in Appendix A.}$$
Equation (30) reduces to (16) for $c_1=0$ and to (28) for $c_\mu=0$ . The equation combines the advantages of (16) and (28). On the one hand, the information from the entire population is used efficiently by the so-called rank- $\mu$ update. On the other hand, information of correlations between generations is exploited by using the evolution path for the rank-one update. The former is important in large populations, the latter is particularly important in small populations.
4 Step-Size Control
The covariance matrix adaptation, discussed in the last section, does not explicitly control the "overall scale" of the distribution, the step-size. The covariance matrix adaptation increases or decreases the scale only in a single direction for each selected step—or it decreases the scale by fading out old information by a given, non-adaptive factor. Less informally, we have two specific reasons to introduce a step-size control in addition to the adaptation rule (30) for C(g) .
- The optimal overall step length cannot be well approximated by (30), in particular if µeff is chosen larger than one.
For example, on fsphere(x) = P^{n} i=1 x 2 i , given C (g) = I and λ ≤ n, the optimal step-size σ equals approximately µ p fsphere(x)/n with equal recombination weights [6, 33] and 1.25 µeffp fsphere(x)/n with optimal recombination weights [4].19 This dependency on µ or µeff can not be realized by (16) or (30).
- The largest reliable learning rate for the covariance matrix update in (30) is too slow to achieve competitive change rates for the overall step length.
To achieve optimal performance on fsphere with an Evolution Strategy with weighted recombination, the overall step length must decrease by a factor of about exp(0.25) ≈ 1.28 within n function evaluations, as can be derived from progress formulas as in [4] and [6, p. 229]. That is, the time horizon for the step length change must be proportional to n or shorter. From the learning rates c^{1} and c^{µ} in (30) follows that the adaptation is too slow to perform competitive on fsphere whenever µeff n. This can be validated by simulations even for moderate dimensions, n ≥ 10, and small µeff ≤ 1 + ln n.
To control the step-size σ (g) we utilize an evolution path, i.e. a sum of successive steps (see also Sect. 3.3.2). The method can be applied independently of the covariance matrix update and is denoted as cumulative path length control, cumulative step-size control, or cumulative step length adaptation (CSA). The length of an evolution path is exploited, based on the following reasoning, as depicted in Fig. 5.
- Whenever the evolution path is short, single steps cancel each other out (Fig. 5, left). Loosely speaking, they are anti-correlated. If steps extinguish each other, the step-size should be decreased.
- Whenever the evolution path is long, the single steps are pointing to similar directions (Fig. 5, right). Loosely speaking, they are correlated. Because the steps are similar, the same distance can be covered by fewer but longer steps into the same directions. In the limit case, when consecutive steps have identical direction, they can be replaced by any of the enlarged single step. Consequently, the step-size should be increased.
- In the desired situation the steps are (approximately) perpendicular in expectation and therefore uncorrelated (Fig. 5, middle).
19Because recombination then reduces the size of the realized step by a factor of õ or õeff (under random selection or in large dimension), the effective optimal steps are proportional to õ or 1.25õeff , respectively.
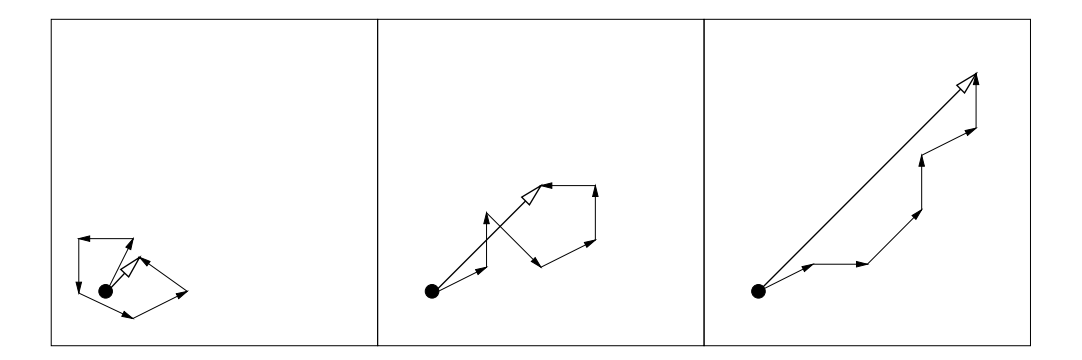
Figure 5: Three evolution paths of respectively six steps from different selection situations (idealized). The lengths of the single steps are all comparable. The length of the evolution paths (sum of steps) is remarkably different and is exploited for step-size control
To decide whether the evolution path is "long" or "short", we compare the length of the path with its expected length under random selection^{20}, where consecutive steps are independent and therefore uncorrelated (uncorrelated steps are the desired situation). If selection biases the evolution path to be longer then expected, $\sigma$ is increased, and, vice versa, if selection biases the evolution path to be shorter than expected, $\sigma$ is decreased. In the ideal situation, selection does not bias the length of the evolution path and the length equals its expected length under random selection.
In practice, to construct the evolution path, $p_{\sigma}$ , the same techniques as in (24) are applied. In contrast to (24), a conjugate evolution path is constructed, because the expected length of the evolution path $p_c$ from (24) depends on its direction (compare (25)). Initialized with $p_{\sigma}^{(0)} = 0$ , the conjugate evolution path reads
$$p_{\sigma}^{(g+1)} = (1 - c_{\sigma})p_{\sigma}^{(g)} + \sqrt{c_{\sigma}(2 - c_{\sigma})\mu_{\text{eff}}} C^{(g)^{-\frac{1}{2}}} \frac{m^{(g+1)} - m^{(g)}}{c_{\text{m}}\sigma^{(g)}} \tag{31} $$
where
$oldsymbol{p}_{\sigma}^{(g)} \in \mathbb{R}^n$ is the conjugate evolution path at generation g.
$c_{\sigma} < 1$ . Again, $1/c_{\sigma}$ is the backward time horizon of the evolution path (compare (20)). For small $\mu_{\rm eff}$ , a time horizon between $\sqrt{n}$ and n is reasonable.
$\sqrt{c_{\sigma}(2-c_{\sigma})\mu_{\rm eff}}$ is a normalization constant, see (24).
$C^{(g)} \stackrel{1}{=} \stackrel{\text{def}}{=} B^{(g)} D^{(g)}^{-1} B^{(g)}^{\mathsf{T}}$ , where $C^{(g)} = B^{(g)} (D^{(g)})^2 B^{(g)}^{\mathsf{T}}$ is an eigendecomposition of $C^{(g)}$ , where $B^{(g)}$ is an orthonormal basis of eigenvectors, and the diagonal elements of the diagonal matrix $D^{(g)}$ are square roots of the corresponding positive eigenvalues (cf. Sect. 0.1).
<sup>20Random selection means that the index $i:\lambda$ (compare (6)) is independent of the value of $\boldsymbol{x}_{i:\lambda}^{(g+1)}$ for all $i=1,\ldots,\lambda$ , e.g. $i:\lambda=i$ .
For $C^{(g)} = I$ , we have $C^{(g)^{-\frac{1}{2}}} = I$ and (31) replicates (24). The transformation $C^{(g)^{-\frac{1}{2}}}$ re-scales the step $m^{(g+1)} - m^{(g)}$ within the coordinate system given by $B^{(g)}$ .
The single factors of the transformation $C^{(g)^{-\frac{1}{2}}} = B^{(g)}D^{(g)^{-1}}B^{(g)^{\mathsf{T}}}$ can be explained as follows (from right to left):
${m B}^{(g)^{\sf T}}$ rotates the space such that the columns of ${m B}^{(g)}$ , i.e. the principal axes of the distribution ${\mathcal N}({m 0},{m C}^{(g)})$ , rotate into the coordinate axes. Elements of the resulting vector relate to projections onto the corresponding eigenvectors.
$D^{(g)^{-1}}$ applies a (re-)scaling such that all axes become equally sized.
${m B}^{(g)}$ rotates the result back into the original coordinate system. This last transformation ensures that the principal axes of the distribution are not rotated by the overall transformation and directions of consecutive steps are comparable.
Consequently, the transformation $C^{(g)^{-\frac{1}{2}}}$ makes the expected length of $p_{\sigma}^{(g+1)}$ independent of its direction, and for any sequence of realized covariance matrices $C^{(g)}_{g=0,1,2,\dots}$ we have under random selection $p_{\sigma}^{(g+1)} \sim \mathcal{N}(\mathbf{0},\mathbf{I})$ , given $p_{\sigma}^{(0)} \sim \mathcal{N}(\mathbf{0},\mathbf{I})$ [13].
To update $\sigma^{(g)}$ , we "compare" $\|p_{\sigma}^{(g+1)}\|$ with its expected length $\mathbb{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\|$ , that is
$$\ln \sigma^{(g+1)} = \ln \sigma^{(g)} + \frac{c_{\sigma}}{d_{\sigma}} \left( \frac{\|\boldsymbol{p}_{\sigma}^{(g+1)}\|}{\mathsf{E}\|\mathcal{N}(\mathbf{0}, \mathbf{I})\|} - 1 \right) , \tag{32}$$
where
$d_{\sigma} \approx 1$ , damping parameter, scales the change magnitude of $\ln \sigma^{(g)}$ . The factor $c_{\sigma}/d_{\sigma}/\mathsf{E} \| \mathcal{N}(\mathbf{0}, \mathbf{I}) \|$ is based on in-depth investigations of the algorithm [13].
$\mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\| = \sqrt{2}\,\Gamma(\frac{n+1}{2})/\Gamma(\frac{n}{2}) \approx \sqrt{n} + \mathcal{O}(1/n)$ , expectation of the Euclidean norm of a $\mathcal{N}(\mathbf{0},\mathbf{I})$ distributed random vector.
For $\|\boldsymbol{p}_{\sigma}^{(g+1)}\| = \mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\|$ the second summand in (32) is zero, and $\sigma^{(g)}$ is unchanged, while $\sigma^{(g)}$ is increased for $\|\boldsymbol{p}_{\sigma}^{(g+1)}\| > \mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\|$ , and $\sigma^{(g)}$ is decreased for $\|\boldsymbol{p}_{\sigma}^{(g+1)}\| < \mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\|$ .
Alternatively, we might use the squared norm $\|p_{\sigma}^{(g+1)}\|^2$ in (32) and compare with its expected value n [5]. In this case (32) would read
$$\ln \sigma^{(g+1)} = \ln \sigma^{(g)} + \frac{c_{\sigma}}{2d_{\sigma}} \left( \frac{\|\boldsymbol{p}_{\sigma}^{(g+1)}\|^{2}}{n} - 1 \right) . \tag{33}$$
This update performs rather similar to (32), while it presumable leads to faster step-size increments and slower step-size decrements.
The step-size change is unbiased on the log scale, because $\mathsf{E}\big[\ln\sigma^{(g+1)}\big|\sigma^{(g)}\big] = \ln\sigma^{(g)}$ for $p_\sigma^{(g+1)} \sim \mathcal{N}(\mathbf{0},\mathbf{I})$ . The role of unbiasedness is discussed in Sect. 5. Equations (31) and (32) cause successive steps of the distribution mean $m^{(g)}$ to be approximately $C^{(g)}$ -conjugate.
In order to show that successive steps are approximately C (g)−1 -conjugate first we remark that (31) and (32) adapt σ such that the length of p (g+1) σ equals approximately EkN (0, I) k. Starting from (EkN (0, I) k) 2 ≈ kp (g+1) σ k = p (g+1) σ T p (g+1) σ = RHS^{T}RHS of (31) and assuming that the expected squared length of C (g)− 1 (m(g+1) − m(g) ) is unchanged by selection (unlike its direction) we get
$$p_{\sigma}^{(g)^{\mathsf{T}}} C^{(g)^{-\frac{1}{2}}} (m^{(g+1)} - m^{(g)}) \approx 0 , \tag{34} $$
and
$$\left(C^{(g)^{\frac{1}{2}}}p_{\sigma}^{(g)}\right)^{\mathsf{T}}C^{(g)^{-1}}\left(m^{(g+1)}-m^{(g)}\right)\approx 0 \tag{35} $$
Given 1/(c^{1} + cµ) 1 and (34) we assume also p (g−1) σ T C (g)− 1 2 (m(g+1) − m(g) ) ≈ 0 and derive
$$\left(\boldsymbol{m}^{(g)} - \boldsymbol{m}^{(g-1)}\right)^{\mathsf{T}} \boldsymbol{C}^{(g)-1} \left(\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}\right) \approx 0 \tag{36} $$
That is, the steps taken by the distribution mean become approximately C (g)−1 -conjugate.
Because σ (g) > 0, (32) is equivalent to
$$\sigma^{(g+1)} = \sigma^{(g)} \exp\left(\frac{c_{\sigma}}{d_{\sigma}} \left(\frac{\|\boldsymbol{p}_{\sigma}^{(g+1)}\|}{\mathsf{E}\|\mathcal{N}(\mathbf{0}, \mathbf{I})\|} - 1\right)\right) \tag{37} $$
The length of the evolution path is an intuitive and empirically well validated goodness measure for the overall step length. For µeff > 1 it is the best measure to our knowledge.21 Nevertheless, it fails to adapt nearly optimal step-sizes on very noisy objective functions [7].
5 Discussion
The CMA-ES is an attractive option for non-linear optimization, if "classical" search methods, e.g. quasi-Newton methods (BFGS) and/or conjugate gradient methods, fail due to a non-convex or rugged search landscape (e.g. sharp bends, discontinuities, outliers, noise, and local optima). Learning the covariance matrix in the CMA-ES is analogous to learning the inverse Hessian matrix in a quasi-Newton method. In the end, any convex-quadratic (ellipsoid) objective function is transformed into the spherical function fsphere. This can reduce the number of f-evaluations needed to reach a target f-value on ill-conditioned and/or non-separable problems by orders of magnitude.
The CMA-ES overcomes typical problems that are often associated with evolutionary algorithms.
- Poor performance on badly scaled and/or highly non-separable objective functions. Equation (30) adapts the search distribution to badly scaled and non-separable problems.
21Recently, two-point adaptation has shown to achieve similar performance [20].
-
- The inherent need to use large population sizes. A typical, however intricate to diagnose reason for the failure of population based search algorithms is the degeneration of the population into a subspace. This is usually prevented by non-adaptive components in the algorithm and/or by a large population size (considerably larger than the problem dimension). In the CMA-ES, the population size can be freely chosen, because the learning rates $c_1$ and $c_\mu$ in (30) prevent the degeneration even for small population sizes, e.g. $\lambda=9$ . Small population sizes usually lead to faster convergence, large population sizes help to avoid local optima.
-
- Premature convergence of the population. Step-size control in (37) prevents the population to converge prematurely. It does not prevent the search to end up in a local optimum.
Therefore, the CMA-ES is highly competitive on a considerable number of test functions [13, 21, 23, 25, 26] and was successfully applied to many real world problems.23
Finally, we discuss a few basic design principles that were applied in the previous sections.
Change rates We refer to a change rate as the expected parameter change per sampled search point, given a certain selection situation. To achieve competitive performance on a wide range of objective functions, the possible change rates of the adaptive parameters need to be adjusted carefully. The CMA-ES separately controls change rates for the mean value of the distribution, m, the covariance matrix, C, and the step-size, $\sigma$ .
- The change rate for the mean value m, relative to the given sample distribution, is determined by $c_{\rm m}$ , and by the parent number and the recombination weights. The larger $\mu_{\rm eff}$ , the smaller is the possible change rate of m.24 Similar holds for most evolutionary algorithms.
- The change rate of the covariance matrix C is explicitly controlled by the learning rates $c_1$ and $c_\mu$ and therefore detached from parent number and population size. The learning rate reflects the model complexity. In evolutionary algorithms, the explicit control of change rates of the covariances, independently of population size and mean change, is a rather unique feature.
- The change rate of the step-size $\sigma$ is explicitly controlled by the damping parameter $d_{\sigma}$ and is in particular independent from the change rate of C. The time constant $1/c_{\sigma} \leq n$ ensures a sufficiently fast change of the overall step length in particular with small population sizes.
<sup>22The same problem can be observed with the downhill simplex method [32] in dimension, say, larger than ten.
<sup>23The author stopped to maintain the growing list of (at the time 120) published references to applications in 2009.
<sup>24Given $\lambda \gg n$ , then the mean change per generation is roughly proportional to $\sigma/\sqrt{\mu_{\rm eff}}$ , while the optimal step-size $\sigma$ is roughly proportional to $\mu_{\rm eff}$ . Therefore, the net change with optimal step-size is proportional to $\sqrt{\mu_{\rm eff}}$ per generation. Now considering the effect on the resulting convergence rate, a closer approximation of the gradient adds another factor of $\sqrt{\mu_{\rm eff}}$ , such that the generational progress rate is proportional to $\mu_{\rm eff}$ . Given $\lambda/\mu_{\rm eff} \approx 4$ , we have the remarkable result that the convergence rate $per\ f$ -evaluation is roughly independent of $\lambda$ .
Invariance Invariance properties of a search algorithm denote identical behavior on a set, or a class of objective functions. Invariance is an important property of the CMA-ES.25 Translation invariance should be taken for granted in continuous domain optimization. Translation invariance means that the search behavior on the function $x \mapsto f(x + a)$ , $x^{(0)} = b - a$ , is independent of $a \in \mathbb{R}^n$ . Further invariances, e.g. invariance to certain linear transformations of the search space, are highly desirable: they imply uniform performance on classes of functions^{26} and therefore allow for generalization of empirical results. In addition to translation invariance, the CMA-ES exhibits the following invariances.
- Invariance to order preserving (i.e. strictly monotonic) transformations of the objective function value. The algorithm only depends on the ranking of function values.
- Invariance to angle preserving (rigid) transformations of the search space (rotation, reflection, and translation) if the initial search point is transformed accordingly.
- Scale invariance if the initial scaling, e.g. $\sigma^{(0)}$ , and the initial search point, $m^{(0)}$ , are chosen accordingly.
- Invariance to a scaling of variables (diagonal invariance) if the initial diagonal covariance matrix $C^{(0)}$ , and the initial search point, $m^{(0)}$ , are chosen accordingly.
- Invariance to any invertible linear transformation of the search space, A, if the initial covariance matrix $C^{(0)} = A^{-1} (A^{-1})^{\mathsf{T}}$ , and the initial search point, $m^{(0)}$ , are transformed accordingly. Together with translation invariance, this can also be referred to as affine invariance, i.e. invariance to affine search space transformations.
Invariance should be a fundamental design criterion for any search algorithm. Together with the ability to efficiently adapt the invariance governing parameters, invariance is a key to competitive performance.
Stationarity or Unbiasedness An important design criterion for a randomized search procedure is unbiasedness of variations of object and strategy parameters [8, 26]. Consider random selection, e.g. the objective function f(x) = r and to be independent of x. Then the population mean is unbiased if its expected value remains unchanged in the next generation, that is $\mathsf{E}\big[m^{(g+1)}\,\big|\,m^{(g)}\,\big] = m^{(g)}$ . For the population mean, stationarity under random selection is a rather intuitive concept. In the CMA-ES, stationarity is respected for all parameters that appear in the basic equation (5). The distribution mean m, the covariance matrix C, and $\ln \sigma$ are unbiased. Unbiasedness of $\ln \sigma$ does not imply that $\sigma$ is unbiased. Under random selection, $\mathsf{E}\big[\sigma^{(g+1)}\,\big|\,\sigma^{(g)}\,\big] > \sigma^{(g)}$ , compare (32).
For distribution variances (or step-sizes) a bias toward increase or decrease entails the risk of divergence or premature convergence, respectively, whenever the selection pressure is low or when no improvements are observed. On noisy problems, a properly controlled bias towards increase can be appropriate. It has the non-negligible disadvantage that the decision for termination becomes more difficult.
$<sup>^{25}\</sup>mbox{Special}$ acknowledgments to Iván Santibáñez-Koref for pointing this out to me.
<sup>26However, most invariances are linked to a state space transformation. Therefore, uniform performance is only observed after the state of the algorithm has been adapted.
<sup>27Alternatively, if (37) were designed to be unbiased for $\sigma^{(g+1)}$ , this would imply that $\mathsf{E} \big[ \ln \sigma^{(g+1)} \, \big| \, \sigma^{(g)} \big] < \ln \sigma^{(g)}$ , in our opinion a less desirable alternative.
Acknowledgments
The author wishes to gratefully thank Anne Auger, Christian Igel, Stefan Kern, and Fabrice Marchal for the many valuable comments on the manuscript.
References
- [1] Akimoto Y, Auger A, Hansen N. Quality gain analysis of the weighted recombination evolution strategy on general convex quadratic functions. In Proceedings of the 14th ACM/SIGEVO Conference on Foundations of Genetic Algorithms (FOGA '17), pages 111–126. ACM, New York, NY, USA, 2017.
- [2] Akimoto Y, Hansen N. Diagonal acceleration for covariance matrix adaptation evolution strategies. Evolutionary computation, 28(3):405–435, 2020.
- [3] Auger A, Hansen N. A restart CMA evolution strategy with increasing population size. In Proceedings of the IEEE Congress on Evolutionary Computation, 2005.
- [4] Arnold DV. Weighted multirecombination evolution strategies. Theoretical computer science, 361.1:18–37, 2006.
- [5] Arnold DV, Beyer HG. Performance analysis of evolutionary optimization with cumulative step length adaptation. IEEE Transactions on Automatic Control, 49(4):617–622, 2004.
- [6] Beyer HG. The Theory of Evolution Strategies. Springer, Berlin, 2001.
- [7] Beyer HG, Arnold DV. Qualms regarding the optimality of cumulative path length control in CSA/CMA-evolution strategies. Evolutionary Computation, 11(1):19–28, 2003.
- [8] Beyer HG, Deb K. On self-adaptive features in real-parameter evolutionary algorithms. IEEE Transactions on Evolutionary Computation, 5(3):250–270, 2001.
- [9] Collange G, Delattre N, Hansen N, Quinquis I, Schoenauer M. Multidisciplinary optimisation in the design of future space launchers. In Breitkopf and Coelho, editors, Multidisciplinary Design Optimization in Computational Mechanics, chapter 12, pages 487–496. Wiley, 2010.
- [10] Dufosse P, Hansen N. Augmented Lagrangian, penalty techniques and surrogate mod- ´ eling for constrained optimization with CMA-ES. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO '21), pages 519–527, 2021.
- [11] Gissler A, Auger A, Hansen N. Learning rate adaptation by line search in evolution strategies with recombination. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO '22), pages 630–638. ACM, New York, NY, USA, 2022.
-
[12] Glasmachers T, Schaul T, Yi S, Wierstra D, Schmidhuber J. Exponential natural evolution strategies. In Proceedings of the 12th annual Genetic and Evolutionary Computation Conference, GECCO, pages 393–400. ACM, 2010.
-
[13] Hansen N. Verallgemeinerte individuelle Schrittweitenregelung in der Evolutionsstrategie. Mensch und Buch Verlag, Berlin, 1998.
- [14] Hansen N. Invariance, self-adaptation and correlated mutations in evolution strategies. In Schoenauer M, Deb K, Rudolph G, Yao X, Lutton E, Merelo JJ, Schwefel HP, editors, Parallel Problem Solving from Nature - PPSN VI, pages 355–364. Springer, 2000.
- [15] Hansen N. The CMA evolution strategy: a comparing review. In Lozano JA, Larranaga P, Inza I, and Bengoetxea E, editors, Towards a new evolutionary computation. Advances on estimation of distribution algorithms, pages 75–102. Springer, 2006.
- [16] Hansen N. Benchmarking a BI-Population CMA-ES on the BBOB-2009 Function Testbed. In the workshop Proceedings of the Genetic and Evolutionary Computation Conference, GECCO, pages 2389–2395. ACM, 2009.
- [17] Hansen N. Variable Metrics in Evolutionary Computation. Habilitation a diriger des ` recherches, Universite Paris-Sud, 2010. ´
- [18] Hansen N. Injecting External Solutions Into CMA-ES. CoRR, arXiv:1110.4181, 2011.
- [19] Hansen N, Auger A. Principled design of continuous stochastic search: From theory to practice. In Y Borenstein and A Moraglio, eds.: Theory and Principled Methods for Designing Metaheustics. Springer, pages 145–180, 2014.
- [20] Hansen N, Atamna A, Auger A. How to Assess Step-Size Adaptation Mechanisms in Randomised Search. In Parallel Problem Solving from Nature – PPSN XIII, pages 60–69. Springer, 2014.
- [21] Hansen N, Kern S. Evaluating the CMA evolution strategy on multimodal test functions. In Xin Yao et al., editors, Parallel Problem Solving from Nature – PPSN VIII, pages 282–291. Springer, 2004.
- [22] Hansen N, Niederberger SPN, Guzzella L, Koumoutsakos P. A method for handling uncertainty in evolutionary optimization with an application to feedback control of combustion. IEEE Transactions on Evolutionary Computation, 13(1):180–197, 2009.
- [23] Hansen N, Muller SD, Koumoutsakos P. Reducing the time complexity of the deran- ¨ domized evolution strategy with covariance matrix adaptation (CMA-ES). Evolutionary Computation, 11(1):1–18, 2003.
- [24] Hansen N, Ostermeier A. Adapting arbitrary normal mutation distributions in evolution strategies: The covariance matrix adaptation. In Proceedings of the 1996 IEEE Conference on Evolutionary Computation (ICEC '96), pages 312–317, 1996.
- [25] Hansen N, Ostermeier A. Convergence properties of evolution strategies with the derandomized covariance matrix adaptation: The (µ/µI , λ)-CMA-ES. In Proceedings of the 5 th European Congress on Intelligent Techniques and Soft Computing, pages 650–654, 1997.
-
[26] Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evolutionary Computation, 9(2):159–195, 2001.
-
[27] Hansen N, Ros R. Benchmarking a weighted negative covariance matrix update on the BBOB-2010 noiseless testbed. In Proceedings companion of the 12th annual Genetic and Evolutionary Computation Conference, GECCO, pages 1673–1680. ACM, 2010.
- [28] Jastrebski G, Arnold DV. Improving evolution strategies through active covariance matrix adaptation. In Proceedings of the 2006 IEEE Congress on Evolutionary Computation, CEC, pages 2814–2821. IEEE, 2006.
- [29] Kern S, Muller SD, Hansen N, B ¨ uche D, Ocenasek J, Koumoutsakos P. Learning proba- ¨ bility distributions in continuous evolutionary algorithms – a comparative review. Natural Computing, 3:77–112, 2004.
- [30] Larranaga P. A review on estimation of distribution algorithms. In P. Larra ˜ naga and J. A. ˜ Lozano, editors, Estimation of Distribution Algorithms, pages 80–90. Kluwer Academic Publishers, 2002.
- [31] Larranaga P, Lozano JA, Bengoetxea E. Estimation of distribution algorithms based ˜ on multivariate normal and Gaussian networks. Technical report, Dept. of Computer Science and Artificial Intelligence, University of the Basque Country, 2001. KZAA-IK-1-01.
- [32] Nelder JA, Mead R. A simplex method for function minimization. The Computer Journal 7.4:308-313, 1965.
- [33] Rechenberg I. Evolutionsstrategie '94. Frommann-Holzboog, Stuttgart, Germany, 1994.
- [34] Rubenstein RY, Kroese DP. The Cross-Entropy Method: a unified approach to combinatorial optimization, Monte-Carlo simulation, and machine learning. Springer, 2004.
- [35] Suttorp T, Hansen N, Igel C. Efficient Covariance Matrix Update for Variable Metric Evolution Strategies. Machine Learning 75(2): 167–197, 2009.
Algorithm Summary: The $(\mu/\mu_W, \lambda)$ -CMA-ES
Figure 6 outlines the complete algorithm^{28}, summarizing (5), (9), (24), (30), (31), and (37). Used symbols, in order of appearance, are:
- $y_k \sim \mathcal{N}(0, C)$ , for $k = 1, \dots, \lambda$ , are realizations from a multivariate normal distribution with zero mean and covariance matrix C.
- B,D result from an eigendecomposition of the covariance matrix C with $C = BD^2B^T$ $BDDB^{\mathsf{T}}$ (cf. Sect. 0.1). Columns of B are an orthonormal basis of eigenvectors. Diagonal elements of the diagonal matrix D are square roots of the corresponding positive eigenvalues. While (39) can certainly be implemented using a Cholesky decomposition of C, the eigendecomposition is needed to correctly compute $C^{-\frac{1}{2}} = BD^{-\hat{1}}B^{\mathsf{T}}$ for (43) and (46).
$x_k \in \mathbb{R}^n$ , for $k = 1, ..., \lambda$ . Sample of $\lambda$ search points.
$\langle y \rangle_{w} = \sum_{i=1}^{\mu} w_{i} y_{i:\lambda}$ , step of the distribution mean disregarding step-size $\sigma$ .
$\mathbf{y}_{i:\lambda} = (\mathbf{x}_{i:\lambda} - \mathbf{m})/\sigma$ , see $\mathbf{x}_{i:\lambda}$ below.
- $x_{i:\lambda} \in \mathbb{R}^n$ , i-th best point out of $x_1, \ldots, x_{\lambda}$ from (40). The index $i:\lambda$ denotes the index of the i-th ranked point, that is $f(\mathbf{x}_{1:\lambda}) \leq f(\mathbf{x}_{2:\lambda}) \leq \cdots \leq f(\mathbf{x}_{\lambda:\lambda})$ .
- $\mu=|\{w_i\,|\,w_i>0\}|=\sum_{i=1}^{\lambda}\mathbf{1}_{(0,\inf)}(w_i)\geq 1$ is the number of strictly positive recombination
- $\mu_{\text{eff}} = \left(\sum_{i=1}^{\mu} w_i^2\right)^{-1}$ is the variance effective selection mass, see (8). Because $\sum_{i=1}^{\mu} |w_i| = 1$ , we have $1 \le \mu_{\text{eff}} \le \mu$ .
- $m{C}^{-\frac{1}{2}} \stackrel{ ext{def}}{=} m{B} m{D}^{-1} m{B}^\mathsf{T}$ , see $m{B}, m{D}$ above. The matrix $m{D}$ can be inverted by inverting its diagonal elements. From the definitions we find that $C^{-\frac{1}{2}}y_i=Bz_i$ , and $C^{-\frac{1}{2}}\langle y \rangle_{_{\mathrm{W}}}=$ $\tilde{\boldsymbol{B}} \sum_{i=1}^{\mu} w_i \, \boldsymbol{z}_{i:\lambda}.$
$\mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\| = \sqrt{2}\,\Gamma(\tfrac{n+1}{2})/\Gamma(\tfrac{n}{2}) \approx \sqrt{n}\,\big(1-\tfrac{1}{4n}+\tfrac{1}{21n^2}\big).$
$h_{\sigma} = \left\{ \begin{array}{ll} 1 & \text{if } \frac{\|p_{\sigma}\|}{\sqrt{1-(1-c_{\sigma})^{2(g+1)}}} < (1.4+\frac{2}{n+1})\mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\,\| \\ 0 & \text{otherwise} \end{array} \right., \text{ where } g \text{ is the generation}$
number. The Heaviside function $h_{\sigma}$ stalls the update of $p_{c}$ in (45) if $||p_{\sigma}||$ is large. This prevents a too fast increase of axes of C in a linear surrounding, i.e. when the step-size is far too small. This is useful when the initial step-size is chosen far too small or when the objective function changes in time.
- $\delta(h_{\sigma}) = (1 h_{\sigma})c_{\rm c}(2 c_{\rm c}) \le 1$ is of minor relevance. In the (unusual) case of $h_{\sigma} = 0$ , it substitutes for the second summand from (45) in (47).
- $\sum w_i = \sum_{i=1}^{\lambda} w_i$ is the sum of the recombination weights, see (49)–(53). We have $-c_1/c_{\mu} \le$ $\sum w_i \le 1$ and for the default population size $\lambda$ , we meet the lower bound $c_{\mu} \sum w_i =$ $-c_1$ .
<sup>28With negative recombination weights in the covariance matrix, chosen here by default, the algorithm is sometimes denoted as aCMA-ES for active CMA [28].
Set parameters
Set parameters λ, wi=1...λ, cm, cσ, dσ, cc, c1, and c^{µ} according to Table 1.
Initialization
Set evolution paths p^{σ} = 0, p^{c} = 0, covariance matrix C = I, and g = 0.
Choose distribution mean m ∈ R n and step-size σ ∈ R>0 problem dependent.1
Until termination criterion met, g ← g + 1
Sample new population of search points, for k = 1, . . . , λ
$$\mathbf{z}_k \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{38} $$
$$y_k = BDz_k \sim \mathcal{N}(0, C) \tag{39} $$
$$\boldsymbol{x}_k = \boldsymbol{m} + \sigma \boldsymbol{y}_k \sim \mathcal{N}(\boldsymbol{m}, \sigma^2 \boldsymbol{C}) \tag{40} $$
Selection and recombination
$$\langle \boldsymbol{y} \rangle_{\mathbf{w}} = \sum_{i=1}^{\mu} w_i \, \boldsymbol{y}_{i:\lambda} \quad \text{where } \sum_{i=1}^{\mu} w_i = 1, \ w_i > 0 \text{ for } i = 1 \dots \mu \tag{41} $$
$$\boldsymbol{m} \leftarrow \boldsymbol{m} + c_{\mathrm{m}} \sigma \langle \boldsymbol{y} \rangle_{\mathrm{w}} \quad \text{equals } \sum_{i=1}^{\mu} w_{i} \, \boldsymbol{x}_{i:\lambda} \text{ if } c_{\mathrm{m}} = 1 \tag{42} $$
Step-size control
$$\boldsymbol{p}_{\sigma} \leftarrow (1 - c_{\sigma})\boldsymbol{p}_{\sigma} + \sqrt{c_{\sigma}(2 - c_{\sigma})\mu_{\text{eff}}} \boldsymbol{C}^{-\frac{1}{2}} \langle \boldsymbol{y} \rangle_{\text{w}} \tag{43} $$
$$\sigma \leftarrow \sigma \times \exp\left(\frac{c_{\sigma}}{d_{\sigma}} \left(\frac{\|\boldsymbol{p}_{\sigma}\|}{\mathsf{E}\|\mathcal{N}(\mathbf{0},\mathbf{I})\|} - 1\right)\right) \tag{44} $$
Covariance matrix adaptation
$$\boldsymbol{p}_{\rm c} \leftarrow (1 - c_{\rm c})\boldsymbol{p}_{\rm c} + h_{\sigma}\sqrt{c_{\rm c}(2 - c_{\rm c})\mu_{\rm eff}} \langle \boldsymbol{y} \rangle_{\rm w} \tag{45} $$
$$w_i^{\circ} = w_i \times (1 \text{ if } w_i \ge 0 \text{ else } n/\|\boldsymbol{C}^{-\frac{1}{2}}\boldsymbol{y}_{i:\lambda}\|^2) \tag{46} $$
$$\boldsymbol{C} \leftarrow (1 + \underbrace{c_1 \delta(h_{\sigma}) - c_1 - c_{\mu} \sum w_j}) \boldsymbol{C} + c_1 \boldsymbol{p}_{c} \boldsymbol{p}_{c}^{\mathsf{T}} + c_{\mu} \sum_{i=1}^{\lambda} w_i^{\circ} \boldsymbol{y}_{i:\lambda} \boldsymbol{y}_{i:\lambda}^{\mathsf{T}} \tag{47} $$
Figure 6: The (µ/µW, λ)-CMA Evolution Strategy. Symbols: see text
1The optimum should presumably be within the initial cube m ± 3σ(1, . . . , 1)T. If the optimum is expected to be in the initial search interval [a, b] n we may choose the initial search point, m, uniformly randomly in [a, b] n, and σ = 0.3(b − a). Different search intervals ∆s^{i} for different variables can be reflected by a different initialization of C, in that the diagonal elements of C obey cii = (∆si) 2 . However, the ∆s^{i} should not disagree by several orders of magnitude. Otherwise a scaling of the variables should be applied.
Default Parameters The (external) strategy parameters are $\lambda$ , $w_{i=1...\lambda}$ , $c_{\rm m}$ , $c_{\sigma}$ , $d_{\sigma}$ , $c_{\rm c}$ , $c_{\rm 1}$ , and $c_{\mu}$ . Default strategy parameter values are given in Table 1. An in-depth discussion of most parameters is given in [26].
The given setting for the default negative weights was introduced in 2016. The setting is somewhere between uniform weights [28] and mirrors of the positive weight values [4, 27]. The choice is a compromise between avoiding increasingly large negative values which lead to a large variance reduction in a single direction in C while still giving emphasis on the selection differences in particular for weights close to the median rank. We attempt to scale all negative weights such that the factor in front of C in (47) becomes 1. That is, we have by default no decay on C and the variance added to the covariance matrix by the positive updates equals, in expectation, to the variance removed by the negative updates.
Specifically, we want to achieve $c_1 + c_{\mu} \sum w_j = 0$ , that is
$$c_1 = -c_{\mu} \sum w_j$$
$$c_1/c_{\mu} = -\left(\sum |w_j|^+ - \sum |w_j|^-\right)$$
$$c_1/c_{\mu} = -1 + \sum |w_j|^-$$
$$1 + c_1/c_{\mu} = \sum |w_j|^- ,$$
hence the multiplier $\alpha_{\mu}^{-}$ in (53) is set to $1 + c_1/c_{\mu}$ .
Choosing $\sum |w_j|^-$ in the order of 1 is only viable if $\mu_{\rm eff} \gg \mu_{\rm eff}^- = \left(\sum_{i=\mu+1}^{\lambda} w_i\right)^2/\sum_{i=\mu+1}^{\lambda} w_i^2$ , that is, if the variance effective update information from positive weights, $\mu_{\rm eff}$ , is not much larger than that from negative weights, $\mu_{\rm eff}^-$ . In the default setting, $\mu_{\rm eff}^-$ is about 1.2 to 1.5 times larger than $\mu_{\rm eff}$ , because the curve $w_i$ versus i flattens out for increasing i. In (53) we use the bound $\alpha_{\mu_{\rm eff}}^-$ , see (51), to (i) get a meaningful value for any choices of $w_i'$ , and (ii) preserve the effect from letting $c_\mu$ go to zero (eventually turning off the covariance matrix adaptation entirely).
The apparent circular dependency between $w_i$ , $\alpha_\mu^-$ , $c_\mu$ , $\mu_{\rm eff}$ , and again $w_i$ can be resolved: the variance effective selection mass $\mu_{\rm eff}$ depends only on the relative relation between the positive weights, such that $\mu_{\rm eff}(w_{1...\lambda}) = \mu_{\rm eff}(w_{1...\mu}) = (\sum_{i=1}^\mu w_i)^2/\sum_{i=1}^\mu w_i^2 = \mu_{\rm eff}(w_{1...\mu}')$ . That is, $\mu_{\rm eff}$ and $\mu_{\rm eff}^-$ can be computed already from $w_i'$ of (49), from which $c_\mu$ can be computed, from which the remaining negative weights $w_i$ can be computed.
Finally, we also bound the negative weights via (53) to guaranty positive definiteness of C via (46), thereby, possibly, re-introducing a decay on C. With the default setting for population size $\lambda$ and the default raw weight values, $\alpha_{\text{pos def}}^-$ in Equation (53) leaves the weights unchanged.
Specifically, to guaranty positive definiteness of the covariance matrix, we can bound the maximal variance subtracted in a single direction by the variance remaining after the decay on C is applied in (47), disregarding any added variance (worst case). Defining $\sum |w_i|^- = \sum_{i=\mu+1}^{\lambda} |w_i|$ to be the sum of the absolute values of all negative weights, and assuming a (Mahalanobis-)variance of n from each negative summand of the weighted sum in (47), we require
$$nc_{\mu} \sum |w_i|^- < 1 - c_1 - \sum w_j c_{\mu} = 1 - c_1 - c_{\mu} + c_{\mu} \sum |w_i|^- \tag{59} $$
Table 1: Default Parameters (in 2016), where $\mu=|\{w_i>0\}|=\lfloor\lambda/2\rfloor$ , $\mu_{\rm eff}=\frac{(\sum_{i=1}^\mu w_i')^2}{\sum_{i=1}^\mu w_i'^2}\in [1,\mu],\ \mu_{\rm eff}^-=\frac{(\sum_{i=\mu+1}^\lambda w_i')^2}{\sum_{i=\mu+1}^\lambda w_i'^2},\ \sum_{i=1}^\mu w_i=1,\ {\rm and}\ \sum|w_j|^+\ {\rm is\ the\ sum\ of\ all\ positive,\ and}\ -\sum|w_j|^-\ {\rm the\ sum\ of\ all\ negative}\ w_j\ -values,\ i.e.,\ \alpha_\mu^-=\sum|w_j'|^-\ge 0.\ {\rm Apart\ from\ }w_i\ {\rm for\ }i>\mu,\ {\rm all\ parameters\ are\ taken\ from\ }[16]\ {\rm with\ only\ minor\ modifications}$
Selection and Recombination:
$$\lambda = 4 + |3 \ln n|$$ can be increased (48)
$$w_i' = \ln \frac{\lambda + 1}{2} - \ln i$$ for $i = 1, \dots, \lambda$ preliminary convex shape (49)
$$\alpha_{\mu}^{-} = 1 + c_1/c_{\mu}$$ let $c_1 + c_{\mu} \sum w_i = c_1 + c_{\mu} - c_{\mu} \sum |w_i|^{-}$ be 0 (50)
$$\alpha_{\mu_{\text{eff}}}^{-} = 1 + \frac{2\mu_{\text{eff}}^{-}}{\mu_{\text{eff}} + 2}$$ bound $\sum |w_i|^{-}$ to be compliant with $c_{\mu}(\mu_{\text{eff}})$ (51)
$$\alpha_{\text{pos def}}^{-} = \frac{1 - c_1 - c_{\mu}}{n c_{\mu}} \qquad \text{bound } \sum |w_i|^{-} \text{ to guaranty positive }$$ definiteness (52)
$$w_{i} = \begin{cases} \frac{1}{\sum |w'_{j}|^{+}} w'_{i} & \text{if } w'_{i} \geq 0 \\ \frac{\min(\alpha_{\mu}^{-}, \alpha_{\mu_{\text{eff}}}^{-}, \alpha_{\text{pos def}}^{-})}{\sum |w'_{i}|^{-}} w'_{i} & \text{if } w'_{i} < 0 \end{cases}$$ positive weights sum to one negative weights usually sum to $-\alpha_{\mu}^{-}$
$$c_{\rm m} = 1 \tag{54}$$
Step-size control:
$$c_{\sigma} = \frac{\mu_{\text{eff}} + 2}{n + \mu_{\text{eff}} + 5}$$
$$d_{\sigma} = 1 + 2 \max\left(0, \sqrt{\frac{\mu_{\text{eff}} - 1}{n + 1}} - 1\right) + c_{\sigma} \tag{55} $$
Covariance matrix adaptation:
$$c_{\rm c} = \frac{4 + \mu_{\rm eff}/n}{n + 4 + 2\mu_{\rm eff}/n} \tag{56}$$
$$c_1 = \frac{\alpha_{\text{cov}}}{(n+1.3)^2 + \mu_{\text{eff}}} \quad \text{with } \alpha_{\text{cov}} = 2 \tag{57} $$
$$c_{\mu} = \min\left(1 - c_1, \alpha_{\text{cov}} \frac{1/4 + \mu_{\text{eff}} + 1/\mu_{\text{eff}} - 2}{(n+2)^2 + \alpha_{\text{cov}}\mu_{\text{eff}}/2}\right) \text{ with } \alpha_{\text{cov}} = 2 \tag{58} $$
Solving for $\sum |w_i|^-$ yields
$$\sum |w_i|^- < \frac{1 - c_1 - c_\mu}{(n - 1)c_\mu} \ . \tag{60}$$
We use $\min(\ldots, \frac{1-c_1-c_\mu}{nc_\mu})$ as multiplier for setting $w_{i=\mu+1...\lambda}$ in (53) and normalize the variance from each respective summand $y_{i:\lambda}y_{i:\lambda}^{\mathsf{T}}$ via (46) to n, thereby bounding the variance reduction from negative weight values to the factor $\frac{n-1}{n}$ .
A Python implementation of the slightly intricate computation of the weights (49)–(53) can be found here.
The cumulation parameter $c_{\rm c}$ for (56) is chosen $\propto 1/n$ . For learning a single direction in (almost) linear time, the setting $c_{\rm c} \propto 1/\sqrt{n}$ seems sufficient [19]. Larger values are in general more robust to avoid feedback oscillations or instabilities and might allow for more freedom in the setting of $c_{\rm 1}$ . However, on the cigar function the relationship between $c_{\rm c}$ times dimension $(c_{\rm c} \times n)$ and the evaluations divided by dimension to reach a given target becomes perfectly invariant with increasing dimension.29
Adopting a technique from [35, Eq. (11)], a generalized setting reads
$$c_{\rm c} = \frac{\alpha_c(n) + (\mu_{\rm eff}/n)^{\beta_c}}{n^{\beta_c} + \alpha_c(n) + 2(\mu_{\rm eff}/n)^{\beta_c}} . \tag{61}$$
With $\alpha_c(n)=10^{1-n^{-1/3}}$ and $\beta_c=1$ , the setting is slightly more robust in larger dimension but remains invariant, see Figure 7. When not all parameters of C are subject to adaptation and $1/c_1=o(n^{1.5})$ , we suspect that $\beta_c<1$ is the reasonable choice. The last summand of the denominator of (61) is chosen such that $c_c$ approaches 1/2 when $\mu_{\rm eff}/n$ approaches infinity.
Similarly, the second summand of the denominator of (58), $\alpha_{\rm cov}\mu_{\rm eff}/2$ , is chosen such that $c_{\mu}$ approaches one when $\alpha_{\rm cov}\mu_{\rm eff}$ approaches 2=2/(2-1) times the first summand.
Another technique, namely setting parameters depending on the degrees of freedom is developed in [2].
The default parameters of (53)–(58) are in particular chosen to be a robust setting and therefore, to our experience, applicable to a wide range of functions to be optimized. We do not recommend to change this setting, apart from increasing the population size $\lambda$ in (48), 30 and possibly decreasing $\alpha_{\rm cov}$ on noisy functions. If the $\lambda$ -dependent default values for $w_i$ are used as given, the population size $\lambda$ has a significant influence on the global search performance [21]. Increasing $\lambda$ usually improves the global search capability and the robustness of the CMA-ES, at the price of a reduced convergence speed. The convergence speed (per function evaluation) decreases at most linearly with $\lambda$ . Independent restarts with increasing population size [3], automated or manually conducted, are a useful policy to perform well on most problems.
B Implementational Concerns
We discuss a few implementational questions.
<sup>29This invariance remains almost perfect when the learning rates $c_1$ and $c_\mu$ are chosen $\propto n^{-1.5}$ instead of $\propto n^{-2}$ ( $\propto n^{-1.5}$ is however not a reliable setting). It changes to about $c_c \times n^{1/2}$ when only the diagonal elements of the covariance matrix are adapted with a learning rate of $\propto 1/n$ .
$<sup>^{30}</sup>$ Decreasing $\lambda$ is not recommended. Too small values have strong adverse effects on the performance.
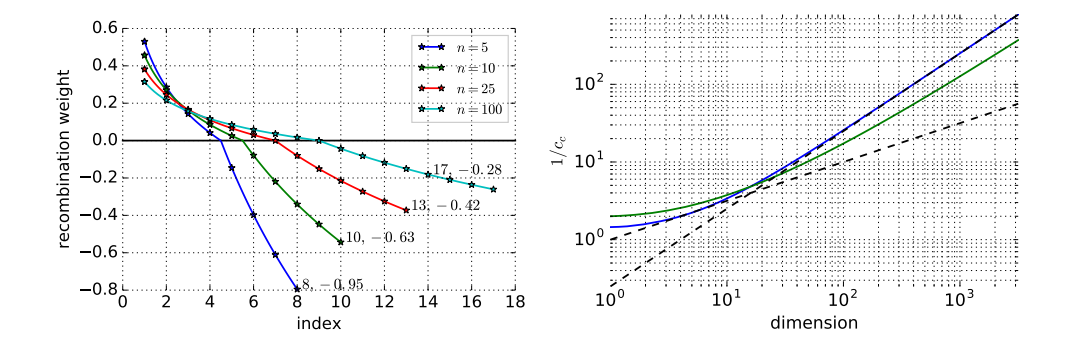
Figure 7: Left: recombination weights from (53) in Table 1 for n=5,10,25,100. Also given are the (default) population size $\lambda$ (corresponding to the last index) and the sum of weights. Positive weights sum to one. Right: backward time horizon $1/c_{\rm c}$ according to (56) (blue) and (61) (green), and n/4 and $\sqrt{n}$ (both dashed) plotted against dimension n. The blue line is above the green line by a factor of about 1.5, 2, 2.5 = 10/4 for $n=100, 1000, \infty$ , respectively.
B.1 Multivariate normal distribution
Let the vector $z \sim \mathcal{N}(\mathbf{0},\mathbf{I})$ have independent, (0,1)-normally distributed components that can easily be sampled on a computer. To generate a random vector $\boldsymbol{y} \sim \mathcal{N}(\mathbf{0},\boldsymbol{C})$ for (39), we set $\boldsymbol{y} = \boldsymbol{B}\boldsymbol{D}\boldsymbol{z}$ (see above symbol descriptions of $\boldsymbol{B}$ and $\boldsymbol{D}$ and Sects. 0.1 and 0.2, and compare lines 52–53 and 83–84 in the source code below). Given $\boldsymbol{y}_k = \boldsymbol{B}\boldsymbol{D}\boldsymbol{z}_k$ and $\boldsymbol{C}^{-\frac{1}{2}} = \boldsymbol{B}\boldsymbol{D}^{-1}\boldsymbol{B}^{\mathsf{T}}$ we have $\boldsymbol{C}^{-\frac{1}{2}}\langle\boldsymbol{y}\rangle_{\mathrm{w}} = \boldsymbol{B}\sum_{i=1}^{\mu}w_i\,\boldsymbol{z}_{i:\lambda}$ (compare (43) and lines 61 and 64 in the source code below).
B.2 Strategy internal numerical effort
In practice, the re-calculation of $\boldsymbol{B}$ and $\boldsymbol{D}$ needs to be done not until about $\max(1, \lfloor 1/(10n(c_1+c_\mu))\rfloor)$ generations. For reasonable $c_1+c_\mu$ values, this reduces the numerical effort due to the eigendecomposition from $\mathcal{O}(n^3)$ to $\mathcal{O}(n^2)$ per generated search point, that is the effort of a matrix vector multiplication.
On a Pentium 4, 2.5 GHz processor the overall strategy internal time consumption is roughly $3 \times (n+5)^2 \times 10^{-8}$ seconds per function evaluation [29].
Remark that it is not sufficient to compute a Cholesky decomposition of C, because then (43) cannot be computed correctly.
B.3 Termination criteria
In general, the algorithm should be stopped whenever it becomes a waste of CPU-time to continue, and it would be better to restart (eventually with increased population size [3]) or to reconsidering the encoding and/or objective function formulation. We recommend the following termination criteria [3, 16] that are mostly related to numerical stability:
- NoEffectAxis: stop if adding a 0.1-standard deviation vector in any principal axis direction of C does not change m. 31
- NoEffectCoord: stop if adding 0.2-standard deviations in any single coordinate does not change m (i.e. m^{i} equals m^{i} + 0.2 σci,i for any i).
- ConditionCov: stop if the condition number of the covariance matrix exceeds 1014 .
- EqualFunValues: stop if the range of the best objective function values of the last 10 + d30n/λe generations is zero.
- Stagnation: we track a history of the best and the median fitness in each iteration over the last 20% but at least 120 + 30n/λ and no more than 20 000 iterations. We stop, if in both histories the median of the last (most recent) 30% values is not better than the median of the first 30%.
- TolXUp: stop if σ×max(diag(D)) increased by more than 104 . This usually indicates a far too small initial σ, or divergent behavior.
Two other useful termination criteria should be considered problem dependent:
- TolFun: stop if the range of the best objective function values of the last 10+d30n/λe generations and all function values of the recent generation is below TolFun. Choosing TolFun depends on the problem, while 10−12 is a conservative first guess.
- TolX: stop if the standard deviation of the normal distribution is smaller than TolX in all coordinates and σp^{c} is smaller than TolX in all components. By default we set TolX to 10−12 times the initial σ.
B.4 Flat fitness
In the case of equal function values for several individuals in the population, it is feasible to increase the step-size (see lines 92–96 in the source code below). This method can interfere with the termination criterion TolFun. In practice, observation of a flat fitness should be rather a termination criterion and consequently lead to a reconsideration of the objective function formulation.
B.5 Boundaries and Constraints
The handling of boundaries and constraints is to a certain extend problem dependent. We discuss a few principles and useful approaches.
Best solution strictly inside the feasible domain If the optimal solution is not too close to the infeasible domain, a simple and sufficient way to handle any type of boundaries and constraints is
31More formally, we terminate if m equals to m + 0.1 σdiibi, where i = (g mod n) + 1, and d 2 ii and b^{i} are respectively the i-th eigenvalue and eigenvector of C, with kbik = 1.
- setting the fitness as
$$f_{\text{fitness}}(\boldsymbol{x}) = f_{\text{max}} + \|\boldsymbol{x} - \boldsymbol{x}_{\text{feasible}}\|$$ , (62)
where fmax is larger than the worst fitness in the feasible population or in the feasible domain (in case of minization) and xfeasible is a constant feasible point, preferably in the middle of the feasible domain.
- re-sampling any infeasible solution x until it become feasible.
Repair available as for example with box-constraints.
Simple repair It is possible to simply repair infeasible individuals before the update equations are applied. This is not recommended, because the CMA-ES makes implicit assumptions on the distribution of solution points, which can be heavily violated by a repair. The main resulting problem might be divergence or too fast convergence of the step-size. However, a (re-)repair of changed or injected solutions for their use in the update seems to solve the problem of divergence [18] (clipping the Mahalanobis distance of the step length to obey kx − mkσ2C ≤ √ n + 2n/(n + 2) seems to be sufficient). Note also that repair mechanisms might be intricate to implement, in particular if y or z are used for implementing the update equations in the original code.
Penalization We evaluate the objective function on a repaired search point, xrepaired, and add a penalty depending on the distance to the repaired solution.
$$f_{\text{fitness}}(\boldsymbol{x}) = f(\boldsymbol{x}_{\text{repaired}}) + \alpha \|\boldsymbol{x} - \boldsymbol{x}_{\text{repaired}}\|^2 \tag{63} $$
The repaired solution is disregarded afterwards.
In case of box-boundaries, xrepaired is set to the feasible solution with the smallest distance kx − xrepairedk. In other words, components that are infeasible in x are set to the (closest) boundary value in xrepaired. A similar boundary handling with a component-wise adaptive α is described in [22].
No repair mechanism available The fitness of the infeasible search point x might similarly compute to
$$f_{\text{fitness}}(\boldsymbol{x}) = f_{\text{offset}} + \alpha \sum_{i} \mathbb{1}_{c_i > 0} \times c_i(\boldsymbol{x})^2 \tag{64} $$
where, w.l.o.g., the (non-linear) constraints c^{i} : R n → R, x 7→ ci(x) are satisfied for ci(x) ≤ 0 , and the indicator function 11ci>0 equals to one for ci(x) > 0, zero otherwise, and foffset = mediankf(xk) equals, for example, to the median or 25%-tile or best function value of the feasible points in the same generation. If no other information is available, ci(x) might be computed as the squared distance of x to the best or the closest feasible solution in the population or the closest known feasible solution. The latter is reminiscent to the boundary repair above. This approach has not yet been experimentally evaluated by the author. A different, slightly more involved approach is given in [9]. Similar and more recent approaches [10] have already found there way into the Python cma package.
In either case of (63) and (64), α should be chosen such that the differences in f and the differences in the second summand have a similar magnitude.
C MATLAB Source Code
This code does not implement negative weights, that is, $w_i = 0$ for $i > \mu$ in Table 1.
1 function xmin=purecmaes
% CMA-ES: Evolution Strategy with Covariance Matrix Adaptation for
3
% nonlinear function minimization.
% This code is an excerpt from cmaes.m and implements the key parts
5
% of the algorithm. It is intendend to be used for READING and
% UNDERSTANDING the basic flow and all details of the CMA *algorithm*.
8
% Computational efficiency is sometimes disregarded.
10
% ----- Initialization ------
11
% User defined input parameters (need to be edited)
12
strfitnessfct = 'felli'; % name of objective/fitness function
13
% number of objective variables/problem dimension
14
N = 10:
xmean = rand(N,1);
% objective variables initial point
15
\begin{array}{llllllllllllllllllllllllllllllllllll
16
% coordinate wise standard deviation (step-size)
17
stopeval = 1e3*N^2; % stop after stopeval number of function evaluations
1.8
19
20
% Strategy parameter setting: Selection
21
22
23
weights = \log (mu+1/2) - \log (1:mu)'; % muXone recombination weights
2.4
mu = floor(mu);
% number of parents/points for recombination
25
weights = weights/sum(weights);
% normalize recombination weights array
mueff=sum(weights)^2/sum(weights.^2); % variance-effective size of mu
26
28
% Strategy parameter setting: Adaptation
29
cc = (4+mueff/N) / (N+4 + 2*mueff/N); % time constant for cumulation for C
cs = (mueff+2)/(N+mueff+5);
3.0
3.1
\texttt{cmu} = \min(1-\texttt{c1}, \ 2\star(\texttt{mueff}-2+1/\texttt{mueff}) \ / \ ((\texttt{N}+2)^2+2\star\texttt{mueff}/2)); \ \ \text{\% for rank-mu update}
33
damps = 1 + 2 \times \max(0, \sqrt{(mueff-1)/(N+1)}) - 1) + cs; % damping for sigma
34
36
% Initialize dynamic (internal) strategy parameters and constants
37
pc = zeros(N, 1); ps = zeros(N, 1); % evolution paths for C and sigma
% B defines the coordinate system
38
B = eve(N);
D = eye(N);
% diagonal matrix D defines the scaling
40
C = B*D*(B*D)';
% covariance matrix
41
eigeneval = 0;
% B and D updated at counteval == 0
42
chiN=N^0.5*(1-1/(4*N)+1/(21*N^2));
% expectation of
43
| | | | | | | | | | = norm(randn(N, 1))
45
% ----- Generation Loop -----
46
47
counteval = 0; % the next 40 lines contain the 20 lines of interesting code
while counteval < stopeval
48
49
50
% Generate and evaluate lambda offspring
51
for k=1:lambda,
52
arz(:,k) = randn(N,1); % standard normally distributed vector
53
arx(:,k) = xmean + sigma * (B*D * arz(:,k)); % add mutation
arfitness(k) = feval(strfitnessfct, arx(:,k)); % objective function call
54
55
counteval = counteval+1;
56
58
% Sort by fitness and compute weighted mean into xmean
[arfitness, arindex] = sort(arfitness); % minimization
59
xmean = arx(:,arindex(1:mu))*weights;
60
63
% Cumulation: Update evolution paths
ps = (1-cs)*ps + (sqrt(cs*(2-cs)*mueff)) * (B * zmean);
hsiq = norm(ps)/sqrt(1-(1-cs)^(2*counteval/lambda))/chiN < 1.4+2/(N+1);
pc = (1-cc)*pc + hsig * sqrt(cc*(2-cc)*mueff) * (B*D*zmean); % Eq. 45
66
67
68
% Adapt covariance matrix C
C = (1-c1-cmu) * C ...
+ c1 * (pc*pc' ...
% Eq. 47
69
% regard old matrix
70
% plus rank one update
+ (1-hsig) * cc*(2-cc) * C) ... % minor correction ... % plus rank mu update
71
72
+ CM11 ...
73
* (B*D*arz(:,arindex(1:mu))) ...
74
* diag(weights) * (B*D*arz(:,arindex(1:mu)))';
75
76
% Adapt step-size sigma
77
sigma = sigma * exp((cs/damps)*(norm(ps)/chiN - 1));
% Eq. 44
78
79
% Update B and D from C
80
if counteval - eigeneval > lambda/(cone+cmu)/N/10 % to achieve O(N^2)
eigeneval = counteval;
81
C=triu(C)+triu(C,1)'; % enforce symmetry
[B,D] = eig(C);
82
83
D = diag(sqrt(diag(D))); % D contains standard deviations now
84
85
end
86
% Break, if fitness is good enough
87
88
if arfitness(1) <= stopfitness
89
break:
90
end
91
% Escape flat fitness, or better terminate?
92
9.3
if arfitness(1) == arfitness(ceil(0.7*lambda))
94
sigma = sigma * exp(0.2+cs/damps);
95
disp('warning: flat fitness, consider reformulating the objective');
96
end
97
disp([num2str(counteval) ': ' num2str(arfitness(1))]);
98
99
100
end % while, end generation loop
101
% ------ Final Message ------
102
103
disp([num2str(counteval) ': ' num2str(arfitness(1))]);
1 0 4
xmin = arx(:, arindex(1)); % Return best point of last generation.
105
106
\mbox{\ensuremath{\$}} Notice that xmean is expected to be even
107
% better.
108
109 % -----
110 function f=felli(x)
111
N = size(x,1); if N < 2 error('dimension must be greater one'); end
f=1e6.^{((0:N-1)/(N-1))} * x.^2; % condition number 1e6
Reformulation of Learning Parameter $c_{cov}$
For sake of consistency and clarity, we have reformulated the learning coefficients in (47) and replaced
$$\frac{c_{\text{cov}}}{\mu_{\text{cov}}}$$ with $c_1$ (65)
$$\frac{c_{\text{cov}}}{\mu_{\text{cov}}} \quad \text{with} \quad c_1$$
$$c_{\text{cov}} \left( 1 - \frac{1}{\mu_{\text{cov}}} \right) \quad \text{with} \quad c_{\mu} \quad \text{and} \tag{65} $$
$$1 - c_{\text{cov}}$$ with $1 - c_1 - c_{\mu}$ , (67)
and chosen (in (57) and (58))
$$c_1 = \frac{2}{(n+1.3)^2 + \mu_{\text{cov}}} \tag{68}$$
$$c_{\mu} = \min \left( 2 \frac{\mu_{\text{cov}} - 2 + \frac{1}{\mu_{\text{cov}}}}{(n+2)^2 + \mu_{\text{cov}}}, 1 - c_1 \right) , \tag{69} $$
The resulting coefficients are quite similar to the previous. In contrast to the previous formulation, $c_1$ becomes monotonic in $\mu_{\text{eff}}^{-1}$ and $c_1 + c_\mu$ becomes virtually monotonic in $\mu_{\text{eff}}$ . Another alternative, depending only on the degrees of freedom in the covariance matrix
and additionally correcting for very small $\lambda$ , reads
$$c_1 = \frac{\min(1, \lambda/6)}{m + 2\sqrt{m} + \frac{\mu_{\text{eff}}}{n}} \tag{70}$$
$$c_{\mu} = \min \left( 1 - c_1, \frac{\alpha_{\mu}^0 + \mu_{\text{eff}} - 2 + \frac{1}{\mu_{\text{eff}}}}{m + 4\sqrt{m} + \frac{\mu_{\text{eff}}}{2}} \right) \tag{71} $$
$$\alpha_{\mu}^{0} = 0.3 , \qquad (72)$$
where $m=\frac{n^2+n}{2}$ is the degrees of freedom in the covariance matrix. For $\mu_{\rm eff}=1$ , the coefficient $c_\mu$ is now chosen to be larger than zero, as $\alpha_\mu^0>0$ . Figure 8 compares the new learning rates with the old ones.
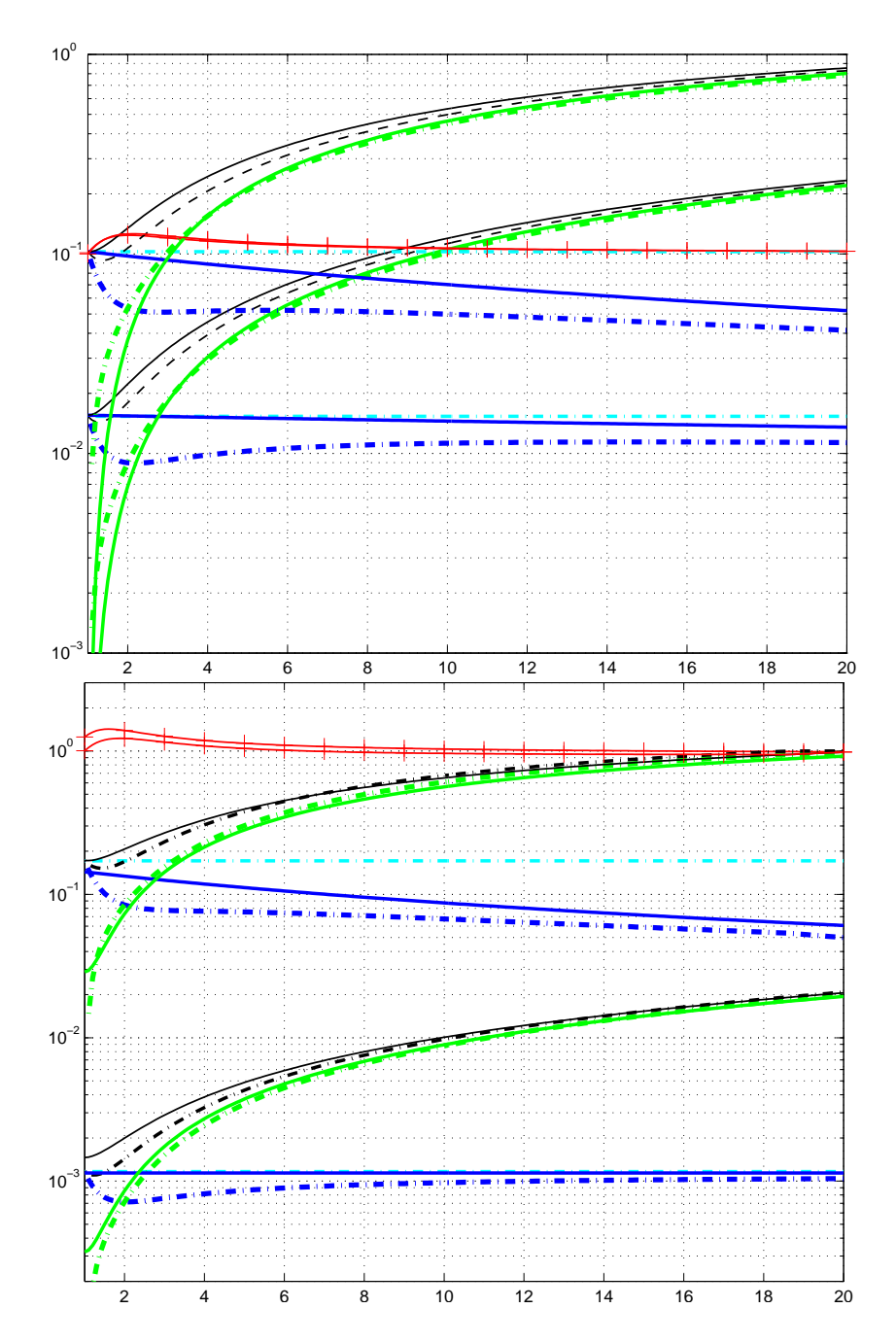
Figure 8: Learning rates $c_1, c_\mu$ (solid) and $c_{\rm cov}$ (dash-dotted) versus $\mu_{\rm eff}$ . Above: Equations (68) etc. for n=3;10. Below: Equations (70) etc. for n=2;40. Black: $c_1+c_\mu$ and $c_{\rm cov}$ ; blue: $c_1$ and $c_{\rm cov}/\mu_{\rm cov}$ ; green: $c_\mu$ and $(1-1/\mu_{\rm cov})c_{\rm cov}$ ; cyan: $2/(n^2+\sqrt{2})$ ; red: $(c_1+c_\mu)/c_{\rm cov}$ , above divided by ten. For $\mu_{\rm cov}\approx 2$ the difference is maximal, because $c_1$ decreases much slower with increasing $\mu_{\rm cov}$ and $c_{\rm cov}$ is non-monotonic in $\mu_{\rm cov}$ (a main reason for the new formulation).