The CMA Evolution Strategy: A Tutorial
作者：Nikolaus Hansen
原文链接：http://arxiv.org/abs/1604.00772v2
Nomenclature
我们采用粗体小写字母 $\boldsymbol{v}$ 表示列向量，粗体大写字母 $\boldsymbol{A}$ 表示矩阵，转置表示为 $\boldsymbol{v}^T$。
缩写
- CMA: Covariance Matrix Adaptation (协方差矩阵自适应)
- EMNA: Estimation of Multivariate Normal Algorithm (多元正态估计算法)
- ES: Evolution Strategy (进化策略)
- ($\mu/\mu_{I,W}, \lambda$)-ES: 具有 $\mu$ 个父代，所有 $\mu$ 个父代参与重组（$I$ 为中间重组，$W$ 为加权重组），以及 $\lambda$ 个后代的进化策略。
- RHS: Right Hand Side (右式)。
希腊符号
- $\lambda \ge 2$: 种群大小，样本大小，后代数量。
- $\mu \le \lambda$: 父代数量，种群中（正向）被选中的搜索点数量，严格正的重组权重数量。
- $\mu_{eff} = (\sum_{i=1}^{\mu} w_i^2)^{-1}$: 均值的方差有效选择质量 (variance effective selection mass)。
- $\sum w_j = \sum_{i=1}^{\lambda} w_i$: 所有权重的和。注意对于 $i > \mu$，$w_i \le 0$。
- $\sum |w_i|^+ = \sum_{i=1}^{\mu} w_i = 1$: 所有正权重的和。
- $\sum |w_i|^- = -(\sum w_j - \sum |w_i|^+) = -\sum_{i=\mu+1}^{\lambda} w_i \ge 0$: 所有负权重之和的相反数。
- $\sigma^{(g)} \in \mathbb{R}_{>0}$: 第 $g$ 代的步长 (step-size)。
拉丁符号
- $\boldsymbol{B} \in \mathbb{R}^{n \times n}$: 一个正交矩阵。$\boldsymbol{B}$ 的列是 $\boldsymbol{C}$ 的单位长度特征向量，对应于 $\boldsymbol{D}$ 的对角元素。
- $\boldsymbol{C}^{(g)} \in \mathbb{R}^{n \times n}$: 第 $g$ 代的协方差矩阵。
- $c_{ii}$: $\boldsymbol{C}$ 的对角元素。
- $c_1 \le 1 - c_\mu$: 协方差矩阵更新中 Rank-One 更新的学习率。
- $c_\mu \le 1 - c_1$: 协方差矩阵更新中 Rank-$\mu$ 更新的学习率。
- $c_\sigma < 1$: 步长控制的累积路径的衰减率。
- $c_c \le 1$: 协方差矩阵 Rank-One 更新的累积路径的衰减率。
- $c_m = 1$: 均值的学习率。
- $\boldsymbol{D} \in \mathbb{R}^{n \times n}$: 一个对角矩阵。$\boldsymbol{D}$ 的对角元素是 $\boldsymbol{C}$ 的特征值的平方根，对应于 $\boldsymbol{B}$ 的各列。
- $d_i > 0$: 对角矩阵 $\boldsymbol{D}$ 的对角元素，$d_i^2$ 是 $\boldsymbol{C}$ 的特征值。
- $d_\sigma \approx 1$: 步长更新的阻尼参数。
- $E$: 期望值。
- $f: \mathbb{R}^n \to \mathbb{R}, \boldsymbol{x} \mapsto f(\boldsymbol{x})$: 待最小化的目标函数（适应度函数）。
- $f_{sphere}: \mathbb{R}^n \to \mathbb{R}, \boldsymbol{x} \mapsto \|\boldsymbol{x}\|^2 = \boldsymbol{x}^T \boldsymbol{x} = \sum_{i=1}^n x_i^2$: 球面函数。
- $g \in \mathbb{N}_0$: 代数计数器，迭代次数。
- $\boldsymbol{I} \in \mathbb{R}^{n \times n}$: 单位矩阵。
- $\boldsymbol{m}^{(g)} \in \mathbb{R}^n$: 第 $g$ 代搜索分布的均值。
- $n \in \mathbb{N}$: 搜索空间维度。
- $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$: 均值为零、协方差矩阵为单位矩阵的多元正态分布。服从 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ 分布的向量具有独立的、(0, 1)-正态分布的分量。
- $\mathcal{N}(\boldsymbol{m}, \boldsymbol{C}) \sim \boldsymbol{m} + \mathcal{N}(\boldsymbol{0}, \boldsymbol{C})$: 均值为 $\boldsymbol{m} \in \mathbb{R}^n$、协方差矩阵为 $\boldsymbol{C} \in \mathbb{R}^{n \times n}$ 的多元正态分布。矩阵 $\boldsymbol{C}$ 是对称正定的。
- $\mathbb{R}_{>0}$: 严格正实数。
- $\boldsymbol{p} \in \mathbb{R}^n$: 进化路径，策略在多代中采取的一系列连续（标准化）步骤。
- $w_i$: 其中 $i = 1, \dots, \lambda$，重组权重。
- $\boldsymbol{x}_k^{(g+1)} \in \mathbb{R}^n$: 第 $g+1$ 代的第 $k$ 个后代/个体。我们也称 $\boldsymbol{x}^{(g+1)}$ 为搜索点，或对象参数/变量，常用的同义词有候选解或设计变量。
- $\boldsymbol{x}_{i:\lambda}^{(g+1)}$: $\boldsymbol{x}_1^{(g+1)}, \dots, \boldsymbol{x}_{\lambda}^{(g+1)}$ 中第 $i$ 好的个体。下标 $i:\lambda$ 表示第 $i$ 个排名的个体的索引，且 $f(\boldsymbol{x}_{1:\lambda}^{(g+1)}) \le f(\boldsymbol{x}_{2:\lambda}^{(g+1)}) \le \dots \le f(\boldsymbol{x}_{\lambda:\lambda}^{(g+1)})$，其中 $f$ 是要最小化的目标函数。
- $\boldsymbol{y}_k^{(g+1)} = (\boldsymbol{x}_k^{(g+1)} - \boldsymbol{m}^{(g)})/\sigma^{(g)}$: 对应于 $\boldsymbol{x}_k = \boldsymbol{m} + \sigma \boldsymbol{y}_k$。
0. Preliminaries
0.1 Eigendecomposition of a Positive Definite Matrix
一个对称正定矩阵 $\boldsymbol{C} \in \mathbb{R}^{n \times n}$ 可以对角化，并且其特征分解遵循： $$ \boldsymbol{C} = \boldsymbol{B}\boldsymbol{D}^2\boldsymbol{B}^T \tag{2} $$
其中$\boldsymbol{B}$ 是一个正交矩阵，$\boldsymbol{D}^2 = \boldsymbol{D}\boldsymbol{D} = \text{diag}(d_1, \dots, d_n)^2 = \text{diag}(d_1^2, \dots, d_n^2)$ 是一个对角矩阵，其对角元素为 $\boldsymbol{C}$ 的特征值。
矩阵分解 (2) 是唯一的（除了 $\boldsymbol{B}$ 中列的符号以及 $\boldsymbol{B}$ 和 $\boldsymbol{D}^2$ 中列的排列顺序），假设所有特征值都不相同。
逆矩阵 $\boldsymbol{C}^{-1}$ 可以通过下式计算： $$ \boldsymbol{C}^{-1} = (\boldsymbol{B}\boldsymbol{D}^2\boldsymbol{B}^T)^{-1} = \boldsymbol{B}^{T^{-1}}\boldsymbol{D}^{-2}\boldsymbol{B}^{-1} = \boldsymbol{B}\boldsymbol{D}^{-2}\boldsymbol{B}^T = \boldsymbol{B}\text{diag}\left(\frac{1}{d_1^2}, \dots, \frac{1}{d_n^2}\right)\boldsymbol{B}^T $$
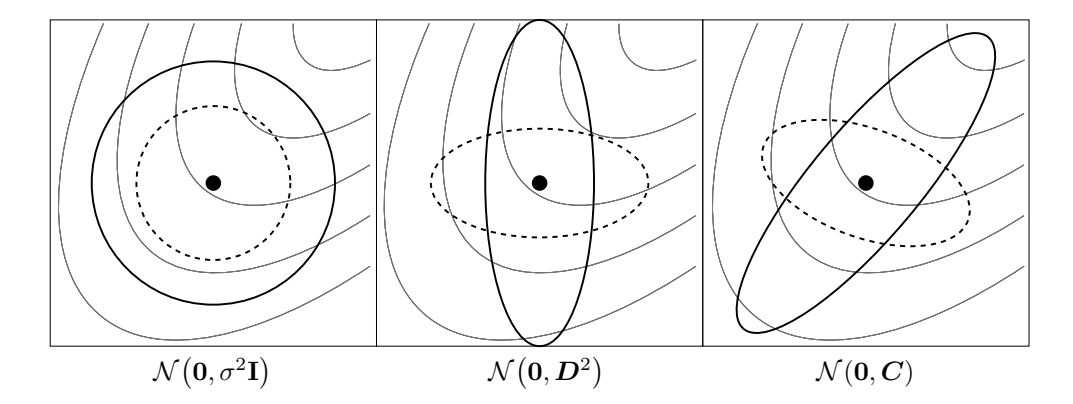图 1: 六种不同正态分布的等密度线椭球体，其中 $\sigma \in \mathbb{R}_{>0}$，$\boldsymbol{D}$ 是对角矩阵，$\boldsymbol{C}$ 是正定全协方差矩阵。细线描绘了可能的目标函数等高线。
我们自然定义 $\boldsymbol{C}$ 的平方根为： $$ \boldsymbol{C}^{\frac{1}{2}} = \boldsymbol{B}\boldsymbol{D}\boldsymbol{B}^T \tag{3} $$ 同样定义 $$ \boldsymbol{C}^{-\frac{1}{2}} = \boldsymbol{B}\boldsymbol{D}^{-1}\boldsymbol{B}^T = \boldsymbol{B} \text{diag}\left(\frac{1}{d_1}, \dots, \frac{1}{d_n}\right)\boldsymbol{B}^T $$
0.2 The Multivariate Normal Distribution
多元正态分布 $\mathcal{N}(\boldsymbol{m}, \boldsymbol{C})$ 具有单峰、“钟形”密度，钟的顶部（众数）对应于分布均值 $\boldsymbol{m}$。分布 $\mathcal{N}(\boldsymbol{m}, \boldsymbol{C})$ 由其均值 $\boldsymbol{m} \in \mathbb{R}^n$ 和对称正定协方差矩阵 $\boldsymbol{C} \in \mathbb{R}^{n \times n}$ 唯一确定。协方差矩阵具有吸引人的几何解释：它们可以唯一地等同于（超）椭球体 $\{\boldsymbol{x} \in \mathbb{R}^n \mid \boldsymbol{x}^T \boldsymbol{C}^{-1}\boldsymbol{x} = 1\}$，如图 1 所示。椭球体是分布的等密度面。椭球体的主轴对应于 $\boldsymbol{C}$ 的特征向量，轴长的平方对应于特征值。特征分解表示为 $\boldsymbol{C} = \boldsymbol{B}\boldsymbol{D}^2\boldsymbol{B}^T$（见 0.1 节）。如果 $\boldsymbol{D} = \sigma \boldsymbol{I}$，其中 $\sigma \in \mathbb{R}_{>0}$ 且 $\boldsymbol{I}$ 表示单位矩阵，则 $\boldsymbol{C} = \sigma^2 \boldsymbol{I}$ 且椭球体是各向同性的（图 1，左）。如果 $\boldsymbol{B} = \boldsymbol{I}$，则 $\boldsymbol{C} = \boldsymbol{D}^2$ 是对角矩阵，椭球体是轴平行取向的（中）。在由 $\boldsymbol{B}$ 的列给出的坐标系中，分布 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C})$ 始终是不相关的。
正态分布 $\mathcal{N}(\boldsymbol{m}, \boldsymbol{C})$ 可以用不同的方式书写： $$ \mathcal{N}(\boldsymbol{m}, \boldsymbol{C}) \sim \boldsymbol{m} + \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \sim \boldsymbol{m} + \boldsymbol{C}^{\frac{1}{2}} \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \sim \boldsymbol{m} + \boldsymbol{B} \boldsymbol{D} \underbrace{\boldsymbol{B}^T \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}_{\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})} \sim \boldsymbol{m} + \boldsymbol{B} \underbrace{\boldsymbol{D} \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}_{\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{D}^2)} \tag{4} $$
其中 “$\sim$” 表示分布相等，且 $\boldsymbol{C} = \boldsymbol{B}\boldsymbol{D}^2\boldsymbol{B}^T$。最后一行可以很好地从右到左解释： * $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ 产生如图 1 左侧所示的球形（各向同性）分布。 * $\boldsymbol{D}$ 在坐标轴内缩放球形分布，如图 1 中间所示。$\boldsymbol{D}\mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{D}^2)$ 具有 $n$ 个独立分量。矩阵 $\boldsymbol{D}$ 可以解释为（个体）步长矩阵，其对角线元素是各分量的标准差。 * $\boldsymbol{B}$ 定义了椭球体的新方向，其中椭球体的新主轴对应于 $\boldsymbol{B}$ 的列。注意 $\boldsymbol{B}$ 具有 $n(n-1)/2$ 个自由度。
方程 (4) 对于计算 $\mathcal{N}(\boldsymbol{m}, \boldsymbol{C})$ 分布的向量非常有用，因为 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ 是一个独立的 (0, 1)-正态分布数的向量，可以很容易地在计算机上实现。
0.3 随机黑盒优化 (Randomized Black Box Optimization)
我们考虑黑盒搜索场景，我们要最小化一个目标函数（或成本函数或适应度函数） $$ f: \mathbb{R}^n \to \mathbb{R}, \quad \boldsymbol{x} \mapsto f(\boldsymbol{x}) $$ 目标是找到一个或多个搜索点（候选解）$\boldsymbol{x} \in \mathbb{R}^n$，使其函数值 $f(\boldsymbol{x})$ 尽可能小。我们不声明寻找全局最优解的目标，因为这在实践中通常既不可行也不相关。黑盒优化指的是这样一种情况：评估搜索点的函数值是关于 $f$ 的唯一可访问信息。待评估的搜索点可以自由选择。我们将搜索成本定义为执行函数评估的次数，换句话说，就是我们需要从 $f$ 获取的信息量。任何性能指标都必须结合所达到的目标函数值来考虑搜索成本。
随机黑盒搜索算法如图 2 所示。在 CMA 进化策略中，搜索分布 $P$ 是多元正态分布。给定所有方差和协方差，正态分布在 $\mathbb{R}^n$ 中的所有分布中具有最大的熵。此外，坐标方向没有任何区别。这两点使得正态分布成为随机搜索的一个特别有吸引力的候选者。
随机搜索算法被认为在崎岖的搜索景观中具有鲁棒性，这些景观可能包含不连续性、（尖锐的）脊或局部最优。特别是协方差矩阵自适应 (CMA) 旨在额外解决病态条件和不可分离的问题。
初始化分布参数 θ^(0)
对于代数 g=0,1,2,...
从分布 P(x|θ^(g)) 采样 λ 个独立点 -> x_1, ..., x_λ
在 f 上评估样本 x_1, ..., x_λ
更新参数 θ^(g+1) = F_θ(θ^(g), (x_1, f(x_1)), ..., (x_λ, f(x_λ)))
如果满足终止条件，则退出
图 2: 随机黑盒搜索。$f: \mathbb{R}^n \to \mathbb{R}$ 是目标函数。
0.4 Hessian 和 协方差矩阵 (Hessian and Covariance Matrices)
我们考虑凸二次目标函数 $f_H: \boldsymbol{x} \mapsto \frac{1}{2}\boldsymbol{x}^T \boldsymbol{H} \boldsymbol{x}$，其中 Hessian 矩阵 $\boldsymbol{H} \in \mathbb{R}^{n \times n}$ 是正定矩阵。给定搜索分布 $\mathcal{N}(\boldsymbol{m}, \boldsymbol{C})$，$\boldsymbol{H}$ 和 $\boldsymbol{C}$ 之间有着密切的关系：在 $f_H$ 上设置 $\boldsymbol{C} = \boldsymbol{H}^{-1}$ 等价于优化各向同性函数 $f_{sphere}(\boldsymbol{x}) = \frac{1}{2}\boldsymbol{x}^T\boldsymbol{x} = \frac{1}{2}\sum_i x_i^2$（其中 $\boldsymbol{H} = \boldsymbol{I}$）且 $\boldsymbol{C} = \boldsymbol{I}$。也就是说，在凸二次目标函数上，将搜索分布的协方差矩阵设置为逆 Hessian 矩阵等价于将椭球函数重新缩放为球形函数。因此，我们假设最优协方差矩阵等于逆 Hessian 矩阵（相差一个常数因子）。此外，选择协方差矩阵或选择相应的搜索空间（即 $\boldsymbol{x}$）仿射线性变换是等价的，因为对于任何满秩 $n \times n$ 矩阵 $\boldsymbol{A}$，我们都能找到一个正定 Hessian 使得 $\frac{1}{2}(\boldsymbol{A}\boldsymbol{x})^T\boldsymbol{A}\boldsymbol{x} = \frac{1}{2}\boldsymbol{x}^T\boldsymbol{A}^T\boldsymbol{A}\boldsymbol{x} = \frac{1}{2}\boldsymbol{x}^T\boldsymbol{H}\boldsymbol{x}$。
协方差矩阵自适应的最终目标是紧密近似目标函数 f 的等高线。在凸二次函数上，这相当于近似逆 Hessian 矩阵，类似于拟牛顿法。
在图 1 中，右图中实线表示的分布最合适地遵循目标函数等高线，很容易预见它将最有助于接近最优解。
正定矩阵 $\boldsymbol{A}$ 的条件数通过欧几里得范数定义：$\text{cond}(\boldsymbol{A}) \stackrel{\text{def}}{=} \|\boldsymbol{A}\| \times \|\boldsymbol{A}^{-1}\|$，其中 $\|\boldsymbol{A}\| = \sup_{\|\boldsymbol{x}\|=1} \|\boldsymbol{A}\boldsymbol{x}\|$。对于正定（Hessian 或协方差）矩阵 $\boldsymbol{A}$，有 $\|\boldsymbol{A}\| = \lambda_{\max}$ 且 $\text{cond}(\boldsymbol{A}) = \frac{\lambda_{\max}}{\lambda_{\min}} \ge 1$，其中 $\lambda_{\max}$ 和 $\lambda_{\min}$ 是 $\boldsymbol{A}$ 的最大和最小特征值。
1. 基本方程：采样 (Basic Equation: Sampling)
在 CMA 进化策略中，通过采样多元正态分布生成新的搜索点（个体，后代）群体。生成代数 $g = 0, 1, 2, \dots$ 的搜索点的基本方程为：
$$ \boldsymbol{x}_{k}^{(g+1)} \sim \boldsymbol{m}^{(g)} + \sigma^{(g)} \mathcal{N} \left( \boldsymbol{0}, \boldsymbol{C}^{(g)} \right) \quad \text{for } k = 1, \dots, \lambda \tag{5} $$
其中： * $\sim$ 表示左侧和右侧分布相同。 * $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(g)})$ 是均值为零且协方差矩阵为 $\boldsymbol{C}^{(g)}$ 的多元正态分布，见 0.2 节。有 $\boldsymbol{m}^{(g)} + \sigma^{(g)}\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(g)}) \sim \mathcal{N}(\boldsymbol{m}^{(g)}, (\sigma^{(g)})^2\boldsymbol{C}^{(g)})$。 * $\boldsymbol{x}_k^{(g+1)} \in \mathbb{R}^n$: 第 $g+1$ 代的第 $k$ 个后代（个体，搜索点）。 * $\boldsymbol{m}^{(g)} \in \mathbb{R}^n$: 第 $g$ 代搜索分布的均值。 * $\sigma^{(g)} \in \mathbb{R}_{>0}$: 第 $g$ 代的“整体”标准差，步长。 * $\boldsymbol{C}^{(g)} \in \mathbb{R}^{n \times n}$: 第 $g$ 代的协方差矩阵。除了标量因子 $(\sigma^{(g)})^2$，$\boldsymbol{C}^{(g)}$ 是搜索分布的协方差矩阵。 * $\lambda \ge 2$: 种群大小，样本大小，后代数量。
为了定义完整的迭代步骤，剩下的问题是如何计算下一代 $g+1$ 的 $\boldsymbol{m}^{(g+1)}$、$\boldsymbol{C}^{(g+1)}$ 和 $\sigma^{(g+1)}$。接下来的三节将分别回答这些问题。附录 A 和 C 分别给出了包含所有参数设置的算法摘要和 MATLAB 源代码。
2. 选择与重组：移动均值 (Selection and Recombination: Moving the Mean)
搜索分布的新均值 $\boldsymbol{m}^{(g+1)}$ 是样本 $\boldsymbol{x}_1^{(g+1)}, \dots, \boldsymbol{x}_\lambda^{(g+1)}$ 中 $\mu$ 个选中点的加权平均：
$$ \boldsymbol{m}^{(g+1)} = \sum_{i=1}^{\mu} w_i \, \boldsymbol{x}_{i:\lambda}^{(g+1)} \tag{6} $$ $$ \sum_{i=1}^{\mu} w_i = 1, \qquad w_1 \ge w_2 \ge \dots \ge w_{\mu} > 0 \tag{7} $$
其中： * $\mu \le \lambda$ 是父代种群大小，即选中点的数量。 * $w_{i=1\dots\mu} \in \mathbb{R}_{>0}$，用于重组的正权重系数。对于 $w_{i=1\dots\mu} = 1/\mu$，方程 (6) 计算 $\mu$ 个选中点的平均值。 * $\boldsymbol{x}_{i:\lambda}^{(g+1)}$: $\boldsymbol{x}_1^{(g+1)}, \dots, \boldsymbol{x}_{\lambda}^{(g+1)}$ 中第 $i$ 好的个体，来自 (5)。下标 $i:\lambda$ 表示第 $i$ 个排名的个体的索引，且 $f(\boldsymbol{x}_{1:\lambda}^{(g+1)}) \le f(\boldsymbol{x}_{2:\lambda}^{(g+1)}) \le \dots \le f(\boldsymbol{x}_{\lambda:\lambda}^{(g+1)})$，其中 $f$ 是要最小化的目标函数。
方程 (6) 通过从 $\lambda$ 个后代点中选择 $\mu < \lambda$ 个来实现截断选择。分配不同的权重 $w_i$ 也应被解释为一种选择机制。方程 (6) 通过考虑 $\mu > 1$ 个个体进行加权平均来实现加权中间重组。
指标 $$ \mu_{\text{eff}} = \left(\frac{\|\boldsymbol{w}\|_{1}}{\|\boldsymbol{w}\|_{2}}\right)^{2} = \frac{\|\boldsymbol{w}\|_{1}^{2}}{\|\boldsymbol{w}\|_{2}^{2}} = \frac{\left(\sum_{i=1}^{\mu} |w_{i}|\right)^{2}}{\sum_{i=1}^{\mu} w_{i}^{2}} = \frac{1}{\sum_{i=1}^{\mu} w_{i}^{2}} \tag{8} $$
将在下文中重复使用，并可解释为选中样本的有效样本大小或方差有效选择质量。根据 (7) 中 $w_i$ 的定义，我们推导出 $1 \le \mu_{\text{eff}} \le \mu$，且当权重相等即 $w_i = 1/\mu$ 时 $\mu_{\text{eff}} = \mu$。
具有不同重组权重的 $\mu_{\text{eff}}$ 的概念在几个方面推广了具有相等重组权重的 $\mu$ 的概念。数量 $\mu$（具有相等重组权重）是使用的信息量，表示为独立源的数量。对独立样本取加权平均值会使原始方差减少 $\mu$ 倍（对于相等权重）和 $\mu_{\text{eff}}$ 倍（对于任意权重），因此 $\mu_{\text{eff}}$ 可以被视为使用信息的数量。为了保持方差不变，平均值必须乘以 $\sqrt{\mu_{\text{eff}}}$。然而，最优步长（给定 $\mu \ll n$）分别与 $\mu$ 成正比（对于相等权重）和与 $1.25\mu_{\text{eff}}$ 成正比（对于最优重组权重），另见第 4 节。
通常，$\mu_{\text{eff}} \approx \lambda/4$ 表示 $w_i$ 的合理设置。一个简单且合理的设置是 $w_i \propto \mu - i + 1$，且 $\mu \approx \lambda/2$，此时 $\mu_{\text{eff}} \approx 3\lambda/8$。
最终方程将 (6) 重写为 $\boldsymbol{m}$ 的更新：
$$ \boldsymbol{m}^{(g+1)} = \boldsymbol{m}^{(g)} + c_{\text{m}} \sum_{i=1}^{\mu} w_i \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)} \right) \tag{9} $$
其中 $c_{\text{m}}$ 是学习率，通常设置为 1。
方程 (9) 推广了 (6)。如果 $c_m \sum_{i=1}^{\mu} w_i = 1$，如默认参数设置的情况（比较附录 A 中的表 1），$-m^{(g)}$ 会抵消 $m^{(g)}$，方程 (9) 和 (6) 是相同的。
在噪声函数上选择 $c_m < 1$ 可能是有利的。在最优步长下，我们要么大致有 $\sigma \propto 1/c_m$，因此 (5) 中的“测试步骤”实际上增加了，而 (9) 中的更新步骤保持不变。然而，太大的测试步骤会对性能产生负面影响，因为排名索引 $i:\lambda$ 是在离（当前）相关区域太远的地方确定的。在单峰和无噪声函数上，任意小的测试步骤（当 $c_m \to \infty$）通常工作良好（在数值精度的限制内）。
3. 协方差矩阵自适应 (Adapting the Covariance Matrix)
本节推导协方差矩阵 $\boldsymbol{C}$ 的更新。我们将从利用一代种群估计协方差矩阵开始（3.1 节）。对于小种群，这种估计是不可靠的，必须发明一种适应程序（Rank-$\mu$-Update，3.2 节）。在极限情况下，每一代只能使用单个点来更新（适应）协方差矩阵（Rank-One-Update，3.3 节）。通过应用累积利用连续步骤之间的依赖关系可以增强这种适应（3.3.2 节）。最后，我们结合 Rank-$\mu$ 和 Rank-One 更新方法（3.4 节）。
3.1 从头估计协方差矩阵 (Estimating the Covariance Matrix From Scratch)
暂时假设种群包含足够的信息来可靠地从种群中估计协方差矩阵。为了方便起见，本节假设 $\sigma^{(g)} = 1$（见 (5)）。对于 $\sigma^{(g)} \neq 1$，除了常数因子外，公式仍然成立。我们可以利用来自 (5) 的采样种群 $\boldsymbol{x}_1^{(g+1)} \dots \boldsymbol{x}_\lambda^{(g+1)}$，通过经验协方差矩阵（重新）估计原始协方差矩阵 $\boldsymbol{C}^{(g)}$：
$$ \boldsymbol{C}_{\text{emp}}^{(g+1)} = \frac{1}{\lambda - 1} \sum_{i=1}^{\lambda} \left( \boldsymbol{x}_{i}^{(g+1)} - \frac{1}{\lambda} \sum_{j=1}^{\lambda} \boldsymbol{x}_{j}^{(g+1)} \right) \left( \boldsymbol{x}_{i}^{(g+1)} - \frac{1}{\lambda} \sum_{j=1}^{\lambda} \boldsymbol{x}_{j}^{(g+1)} \right)^T \tag{10} $$
经验协方差矩阵 $\boldsymbol{C}_{\text{emp}}^{(g+1)}$ 是 $\boldsymbol{C}^{(g)}$ 的无偏估计量：假设 $\boldsymbol{x}_i^{(g+1)}, i = 1 \dots \lambda$ 是随机变量（而不是实现的样本），我们有 $E[\boldsymbol{C}_{\text{emp}}^{(g+1)}] = \boldsymbol{C}^{(g)}$。现在考虑一种稍有不同的方法来获得 $\boldsymbol{C}^{(g)}$ 的估计量。
$$ \boldsymbol{C}_{\lambda}^{(g+1)} = \frac{1}{\lambda} \sum_{i=1}^{\lambda} \left( \boldsymbol{x}_{i}^{(g+1)} - \boldsymbol{m}^{(g)} \right) \left( \boldsymbol{x}_{i}^{(g+1)} - \boldsymbol{m}^{(g)} \right)^T \tag{11} $$
矩阵 $\boldsymbol{C}_{\lambda}^{(g+1)}$ 也是 $\boldsymbol{C}^{(g)}$ 的无偏估计量。(10) 和 (11) 之间的显著区别是参考均值。(10) 中使用的是实际实现样本的均值，而 (11) 中使用的是采样分布的真实均值 $\boldsymbol{m}^{(g)}$（见 (5)）。因此，估计量 $\boldsymbol{C}_{\text{emp}}^{(g+1)}$ 和 $\boldsymbol{C}_{\lambda}^{(g+1)}$ 可以有不同的解释：$\boldsymbol{C}_{\text{emp}}^{(g+1)}$ 估计采样点内部的分布方差，而 $\boldsymbol{C}_{\lambda}^{(g+1)}$ 估计采样步骤 $\boldsymbol{x}_i^{(g+1)} - \boldsymbol{m}^{(g)}$ 的方差。
(10) 和 (11) 之间的一个细微差别是不同的归一化 $\frac{1}{\lambda-1}$ 与 $\frac{1}{\lambda}$，这是在这两种情况下获得无偏估计量所必需的。在 (10) 中，内部求和已经占用了一个自由度。为了获得最大似然估计量，两种情况下都必须使用 $\frac{1}{\lambda}$。
方程 (11) 重新估计原始协方差矩阵。为了“估计”一个“更好”的协方差矩阵，使用了与 (6) 相同的加权选择机制。
$$ \boldsymbol{C}_{\mu}^{(g+1)} = \sum_{i=1}^{\mu} w_i \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)} \right) \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)} \right)^T \tag{12} $$
矩阵 $\boldsymbol{C}_{\mu}^{(g+1)}$ 是选中步骤分布的估计量，就像 $\boldsymbol{C}_{\lambda}^{(g+1)}$ 是选择前原始步骤分布的估计量一样。从 $\boldsymbol{C}_{\mu}^{(g+1)}$ 采样倾向于重现选中的，即成功的步骤，这为“更好”的协方差矩阵的含义提供了理由。
我们将 (12) 与 Estimation of Multivariate Normal Algorithm $\text{EMNA}_{global}$ 进行比较。$\text{EMNA}_{global}$ 中的协方差矩阵类似于 (10)，读作：
$$ \boldsymbol{C}_{\text{EMNA}_{global}}^{(g+1)} = \frac{1}{\mu} \sum_{i=1}^{\mu} \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g+1)} \right) \left( \boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g+1)} \right)^T \tag{13} $$
其中 $\boldsymbol{m}^{(g+1)} = \frac{1}{\mu} \sum_{i=1}^{\mu} \boldsymbol{x}_{i:\lambda}^{(g+1)}$。类似地，将所谓的交叉熵方法应用于连续域优化产生的协方差矩阵为 $\frac{\mu}{\mu-1} \boldsymbol{C}_{\text{EMNA}_{global}}^{(g+1)}$，即 $\mu$ 个最佳点的无偏经验协方差矩阵。在这两种情况下，与 (12) 的微妙但最重要的区别同样是参考均值的选择。方程 (13) 估计选中种群内部的方差，而 (12) 估计选中的步骤。方程 (13) 显示的方差总是小于 (12)，因为其参考均值是方差的最小化器。此外，在大多数可想到的选择情况下，(13) 相比 $\boldsymbol{C}^{(g)}$ 会减小方差。
图 3 展示了在 $\lambda=150, \mu=50$ 和 $w_i=1/\mu$ 的情况下，线性目标函数上的估计结果。给定通常的父代数量 $\mu$ 和重组权重 $w_1,\dots,w_\mu$ 设置，方程 (12) 几何级数地增加了梯度方向上的期望方差（选择发生的地方，这里是其对角线）。方程 (13) 总是几何级数快地减少梯度方向的方差！因此，(13) 非常容易导致过早收敛，特别是在小父代种群中，那时不能指望种群在任何时候都能包围最优解。然而，对于大种群中的大 $\mu$ 值和大的初始方差，不同参考均值的影响可能变得微不足道。
为了确保通过 (5), (6) 和 (12)，$\boldsymbol{C}_{\mu}^{(g+1)}$ 是一个可靠的估计量，方差有效选择质量 $\mu_{\text{eff}}$（参考 (8)）必须足够大：在 $f_{\text{sphere}}(\boldsymbol{x}) = \sum_{i=1}^n x_i^2$ 上使 $\boldsymbol{C}_{\mu}^{(g)}$ 的条件数（参考 0.4 节）小于 10，需要 $\mu_{\text{eff}} \approx 10n$。下一步是规避对 $\mu_{\text{eff}}$ 的这种限制。
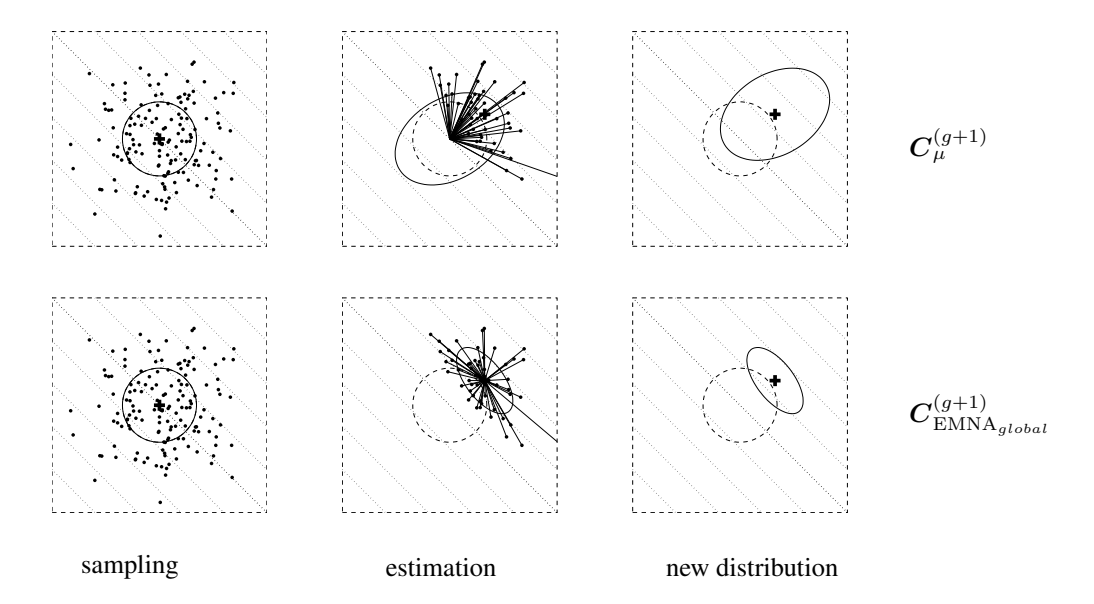图 3: 在需最小化的 $f_{\text{linear}}(\boldsymbol{x}) = -\sum_{i=1}^2 x_i$ 上协方差矩阵的估计。等高线（虚线）表明策略应向右上角移动。上方：根据 (12) 估计 $\boldsymbol{C}_{\mu}^{(g+1)}$，其中 $w_i = 1/\mu$。下方：根据 (13) 估计 $\boldsymbol{C}_{\text{EMNA}_{global}}^{(g+1)}$。左：$\lambda = 150$ 个 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ 分布点的样本。中：$\mu = 50$ 个选中点（点）决定了估计方程的条目（实直线）。右：下一代的搜索分布（实椭球体）。给定 $w_i = 1/\mu$，通过 $\boldsymbol{C}_{\mu}^{(g+1)}$ 的估计对于所有 $\mu < \lambda/2$ 增加了梯度方向的期望方差，而通过 $\boldsymbol{C}_{\text{EMNA}_{global}}^{(g+1)}$ 的估计对于任何 $\mu < \lambda$ 都会几何级数快地减少此方差。
3.2 Rank-$\mu$-Update
为了实现快速搜索（相对于更鲁棒或更全局的搜索），例如在 $f_{\text{sphere}}: \boldsymbol{x} \mapsto \sum x_i^2$ 上的竞争性能，种群大小 $\lambda$ 必须很小。因为典型地（且理想地）$\mu_{\text{eff}} \approx \lambda/4$，所以 $\mu_{\text{eff}}$ 也必须很小，我们可能假设例如 $\mu_{\text{eff}} \le 1 + \ln n$。那么，就不可能从 (12) 中获得良好协方差矩阵的可靠估计量。作为补救措施，额外使用了来自前几代的信息。例如，在足够多的代数之后，所有代估计的协方差矩阵的均值
$$ \boldsymbol{C}^{(g+1)} = \frac{1}{g+1} \sum_{i=0}^{g} \frac{1}{\sigma^{(i)^2}} \boldsymbol{C}_{\mu}^{(i+1)} \tag{14} $$
成为选中步骤的可靠估计量。为了使来自不同代数的 $\boldsymbol{C}_{\mu}^{(g)}$ 具有可比性，纳入了不同的 $\sigma^{(i)}$。（假设 $\sigma^{(i)} = 1$，(14) 类似于来自 Estimation of Multivariate Normal Algorithm $\text{EMNA}_{i}$ 的协方差矩阵。）
在 (14) 中，所有代步骤具有相同的权重。为了给最近的代分配更高的权重，引入了指数平滑。选择 $\boldsymbol{C}^{(0)} = \boldsymbol{I}$ 为单位矩阵，学习率为 $0 < c_\mu \le 1$，那么 $\boldsymbol{C}^{(g+1)}$ 读作
$$ \boldsymbol{C}^{(g+1)} = (1 - c_{\mu})\boldsymbol{C}^{(g)} + c_{\mu} \frac{1}{\sigma^{(g)^{2}}} \boldsymbol{C}_{\mu}^{(g+1)} $$ $$ = (1 - c_{\mu})\boldsymbol{C}^{(g)} + c_{\mu} \sum_{i=1}^{\mu} w_{i} \boldsymbol{y}_{i:\lambda}^{(g+1)} \boldsymbol{y}_{i:\lambda}^{(g+1)^T}, \tag{15} $$
其中 * $c_{\mu} \le 1$ 更新协方差矩阵的学习率。对于 $c_{\mu} = 1$，不保留先验信息，且 $\boldsymbol{C}^{(g+1)} = \frac{1}{\sigma^{(g)^2}} \boldsymbol{C}_{\mu}^{(g+1)}$。对于 $c_{\mu} = 0$，不发生学习，且 $\boldsymbol{C}^{(g+1)} = \boldsymbol{C}^{(0)}$。这里，$c_{\mu} \approx \min(1, \mu_{\text{eff}}/n^2)$ 是一个合理的选择。 * $w_{1...\mu} \in \mathbb{R}$ 使得 $w_1 \ge \dots \ge w_{\mu} > 0$ 且 $\sum_i w_i = 1$。 * $\boldsymbol{y}_{i:\lambda}^{(g+1)} = (\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)})/\sigma^{(g)}$。 * $\boldsymbol{z}_{i:\lambda}^{(g+1)} = \boldsymbol{C}^{(g)^{-\frac{1}{2}}} \boldsymbol{y}_{i:\lambda}^{(g+1)}$ 是变异向量，表示在采样是各向同性的唯一坐标系中，且相应的坐标系变换不旋转分布的原始主轴。
这种协方差矩阵更新称为 Rank-$\mu$-update，因为 (15) 中外积的和的秩为 $\min(\mu, n)$，概率为 1（给定 $\mu$ 个非零权重）。如果 $\mu = 1$，这个和甚至可以只由一项组成。
最后，我们将 (15) 推广到 $\lambda$ 个权重值，它们既不需要和为 1，也不再是非负的，
$$ \boldsymbol{C}^{(g+1)} = (1 - c_{\mu} \sum w_{i}) \boldsymbol{C}^{(g)} + c_{\mu} \sum_{i=1}^{\lambda} w_{i} \boldsymbol{y}_{i:\lambda}^{(g+1)} \boldsymbol{y}_{i:\lambda}^{(g+1)^T} $$ $$ = \boldsymbol{C}^{(g)^{1/2}} \left( \boldsymbol{I} + c_{\mu} \sum_{i=1}^{\lambda} w_{i} \left( \boldsymbol{z}_{i:\lambda}^{(g+1)} \boldsymbol{z}_{i:\lambda}^{(g+1)^T} - \boldsymbol{I} \right) \right) \boldsymbol{C}^{(g)^{1/2}} \tag{16} $$
其中 * $w_{1...\lambda} \in \mathbb{R}$ 使得 $w_1 \ge \dots \ge w_{\mu} > 0 \ge w_{\mu+1} \ge w_{\lambda}$，通常 $\sum_{i=1}^{\mu} w_i = 1$ 且 $\sum_{i=1}^{\lambda} w_i \approx 0$。 * $\sum w_i = \sum_{i=1}^{\lambda} w_i$。
(16) 的第二行在自然坐标系中表达了更新，这一想法已经在其他文献中被考虑过。单位协方差矩阵被更新，之后通过在两侧乘以 $\boldsymbol{C}^{(g)^{1/2}}$ 应用坐标系变换。方程 (16) 使用 $\lambda$ 个权重 $w_i$，其中约一半是负的。如果权重的选择使得 $\sum w_i = 0$，则 $\boldsymbol{C}^{(g)}$ 上的衰减消失，变化仅沿着实现样本的轴进行。
协方差矩阵更新中的负重组权重值在 Jastrebski 和 Arnold 的开创性论文中作为主动协方差矩阵自适应被引入。非相等的负权重值在文献中与相当复杂的机制一起使用，以弥补不同的向量长度。附录 A 表 1 中定义的默认重组权重介于这两个提议之间。稍后与 (16) 略有偏差的是，与负权重关联的向量长度将被重新缩放到（方向相关的）常数，见附录 A 中的 (46) 和 (47)。这允许保证 $\boldsymbol{C}^{(g+1)}$ 的正定性。方便的是，它也减轻了选择误差，这种误差通常使得与较长向量关联的方向看起来比实际更糟糕。
数值 $1/c_{\mu}$ 是向后时间视界 (backward time horizon)，贡献了大约 63% 的整体信息。
因为 (16) 扩展为加权和
$$ \boldsymbol{C}^{(g+1)} = (1 - c_{\mu})^{g+1} \boldsymbol{C}^{(0)} + c_{\mu} \sum_{i=0}^{g} (1 - c_{\mu})^{g-i} \frac{1}{\sigma^{(i)}} \boldsymbol{C}_{\mu}^{(i+1)} , \tag{17} $$
累积了大约 63% 总权重的向后时间视界 $\Delta g$ 定义为
$$ c_{\mu} \sum_{i=g+1-\Delta g}^{g} (1 - c_{\mu})^{g-i} \approx 0.63 \approx 1 - \frac{1}{e} \tag{18} $$
解析求和得出 $$ (1 - c_{\mu})^{\Delta g} \approx \frac{1}{e} , \tag{19} $$ 使用泰勒近似解析 $\Delta g$ 得出 $$ \Delta g \approx \frac{1}{c_{\mu}} \tag{20} $$
也就是说，$\boldsymbol{C}^{(g+1)}$ 中大约 37% 的信息早于 $1/c_{\mu}$ 代，并且根据 (19)，在经过大约 $1/c_{\mu}$ 代之后，原始权重减少了 0.37 倍。
$c_{\mu}$ 的选择至关重要。小值导致学习缓慢，太大的值导致失败，因为协方差矩阵退化。幸运的是，一个好的设置似乎在很大程度上独立于要优化的函数。好的选择的一阶近似是 $c_{\mu} \approx \mu_{\text{eff}}/n^2$。因此，(16) 的特征时间视界大致为 $n^2/\mu_{\text{eff}}$。
实验表明，$c_{\mu} \approx \mu_{\text{eff}}/n^2$ 对于大的 $n$ 值是一个相当保守的设置，而 $\mu_{\text{eff}}/n^{1.5}$ 似乎略微超出了稳定性的极限。指数的最佳但鲁棒的选择仍然是一个悬而未决的问题。
即使对于学习率 $c_{\mu} = 1$，适应协方差矩阵也无法在一代内完成。原始样本分布的影响直到足够多的代数后才会消失。假设固定的搜索成本（函数评估次数），较小的种群大小 $\lambda$ 允许较多的代数，因此通常会导致协方差矩阵更快的适应。
3.3 Rank-One-Update
在 3.1 节中，我们开始使用单一代的所有选中步骤从头估计完整的协方差矩阵。现在我们采取相反的观点。我们仅使用单个选中步骤在代序列中重复更新协方差矩阵。首先，这个观点将给出协方差矩阵适应规则 (16) 的另一个理由。其次，我们将引入所谓的进化路径，最终用于协方差矩阵的 rank-one 更新。
3.3.1 一个不同的视角
我们考虑一种产生 $n$ 维零均值正态分布的具体方法。设向量 $\boldsymbol{y}_1, \dots, \boldsymbol{y}_{g_0} \in \mathbb{R}^n$，$g_0 \ge n$，张成 $\mathbb{R}^n$，且让 $\mathcal{N}(0,1)$ 表示独立的 (0,1)-正态分布随机数，那么
$$ \mathcal{N}(0,1) \boldsymbol{y}_1 + \dots + \mathcal{N}(0,1) \boldsymbol{y}_{g_0} \sim \mathcal{N}\left(\boldsymbol{0}, \sum_{i=1}^{g_0} \boldsymbol{y}_i \boldsymbol{y}_i^T\right) \tag{21} $$
是一个具有零均值和协方差矩阵 $\sum_{i=1}^{g_0} \boldsymbol{y}_i \boldsymbol{y}_i^T$ 的正态分布随机向量。随机向量 (21) 是通过添加“线分布” $\mathcal{N}(0,1) \boldsymbol{y}_i$ 生成的。奇异分布 $\mathcal{N}(0,1) \boldsymbol{y}_i \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{y}_i \boldsymbol{y}_i^T)$ 以最大似然生成向量 $\boldsymbol{y}_i$（考虑所有零均值正态分布）。
生成向量 $\boldsymbol{y}$ 具有最大似然的线分布必须“生活”在包含 $\boldsymbol{y}$ 的线上，因此该分布必须服从 $\mathcal{N}(0,1)\sigma\boldsymbol{y} \sim \mathcal{N}(0,\sigma^2\boldsymbol{y}\boldsymbol{y}^T)$。任何其他零均值线分布根本无法生成 $\boldsymbol{y}$。选择 $\sigma$ 归结为为一维高斯 $\mathcal{N}(0,\sigma^2\|\boldsymbol{y}\|^2)$ 选择 $\|\boldsymbol{y}\|$ 的最大似然，即 $\sigma=1$。
协方差矩阵 $\boldsymbol{y}\boldsymbol{y}^T$ 的秩为 1，其唯一的特征向量是 $\{\alpha \boldsymbol{y} \mid \alpha \in \mathbb{R}_{\setminus 0}\}$，特征值为 $\|\boldsymbol{y}\|^2$。使用方程 (21)，如果适当地选择 $\boldsymbol{y}_i$，则可以实现任何正态分布。例如，(21) 类似于 (4)，使用正交特征向量 $\boldsymbol{y}_i=d_{ii}\boldsymbol{b}_i$，对于 $i=1,\dots,n$，其中 $\boldsymbol{b}_i$ 是 $\boldsymbol{B}$ 的列。一般来说，向量 $\boldsymbol{y}_i$ 不需要是协方差矩阵的特征向量，而且通常也不是。
考虑 (21) 和 (16) 的略微简化，我们试图深入了解协方差矩阵的适应规则。设 (16) 中的求和仅由一项组成（例如 $\mu=1$），且设 $\boldsymbol{y}_{g+1}=\frac{\boldsymbol{x}_{1:\lambda}^{(g+1)}-\boldsymbol{m}^{(g)}}{\sigma^{(g)}}$。那么，协方差矩阵的 rank-one 更新读作
$$ \boldsymbol{C}^{(g+1)} = (1-c_1)\boldsymbol{C}^{(g)} + c_1 \boldsymbol{y}_{g+1}\boldsymbol{y}_{g+1}^T \tag{22} $$
右侧的加项秩为 1，并将 $\boldsymbol{y}_{g+1}$ 的最大似然项添加到协方差矩阵 $\boldsymbol{C}^{(g)}$ 中。因此，下一代生成 $\boldsymbol{y}_{g+1}$ 的概率增加。
(22) 的前两个迭代步骤的示例如图 4 所示。分布 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(1)})$ 倾向于以比初始分布 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ 更大的概率重现 $\boldsymbol{y}_1$；分布 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(2)})$ 倾向于以比 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(1)})$ 更大的概率重现 $\boldsymbol{y}_2$，依此类推。当 $\boldsymbol{y}_1, \dots, \boldsymbol{y}_g$ 表示先前选择的、有利的步骤时，$\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(g)})$ 倾向于重现这些步骤。该过程导致搜索分布 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(g)})$ 与选中的步骤分布对齐。如果两个分布变得相似，如在随机选择下，预期协方差矩阵不会发生进一步变化。
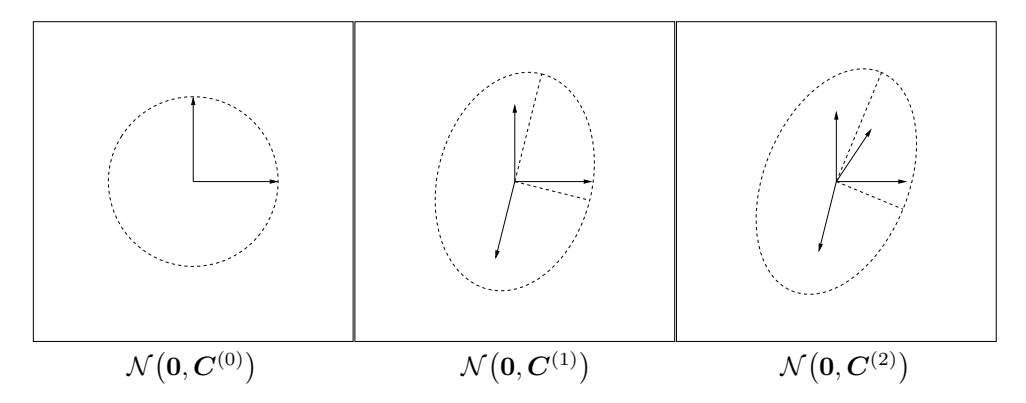图 4: 根据协方差矩阵更新 (22) 的分布变化。左：向量 $e_1$ 和 $e_2$，以及 $\boldsymbol{C}^{(0)} = \boldsymbol{I} = e_1 e_1^T + e_2 e_2^T$。中：向量 $0.91 e_1$, $0.91 e_2$, 和 $0.41 y_1$（系数推导自 $c_1 = 0.17$），以及 $\boldsymbol{C}^{(1)} = (1 - c_1) \boldsymbol{I} + c_1 y_1 y_1^T$，其中 $y_1 = \begin{pmatrix} -0.59 \\ -2.2 \end{pmatrix}$。分布椭球体沿 $y_1$ 方向拉长，从而增加了 $y_1$ 的似然。右：$\boldsymbol{C}^{(2)} = (1 - c_1) \boldsymbol{C}^{(1)} + c_1 y_2 y_2^T$，其中 $y_2 = \begin{pmatrix} 0.97 \\ 1.5 \end{pmatrix}$。
3.3.2 累积：利用进化路径 (Cumulation: Utilizing the Evolution Path)
我们使用了选中步骤 $\boldsymbol{y}_{i:\lambda}^{(g+1)} = (\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)})/\sigma^{(g)}$ 来更新 (16) 和 (22) 中的协方差矩阵。因为 $\boldsymbol{y}\boldsymbol{y}^T = -\boldsymbol{y}(-\boldsymbol{y})^T$，步骤的符号对于协方差矩阵的更新是无关紧要的——也就是说，在计算 $\boldsymbol{C}^{(g+1)}$ 时符号信息丢失了。为了重新引入符号信息，构建了所谓的进化路径。
我们将策略在多代中采取的一系列连续步骤称为进化路径。进化路径可以表示为连续步骤的总和。这种求和称为累积。为了构建进化路径，忽略步长 $\sigma$。例如，可以通过求和构建三个分布均值 $\boldsymbol{m}$ 的步骤的进化路径：
$$ \frac{\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}}{\sigma^{(g)}} + \frac{\boldsymbol{m}^{(g)} - \boldsymbol{m}^{(g-1)}}{\sigma^{(g-1)}} + \frac{\boldsymbol{m}^{(g-1)} - \boldsymbol{m}^{(g-2)}}{\sigma^{(g-2)}} \tag{23} $$
在实践中，为了构建进化路径 $\boldsymbol{p}_c \in \mathbb{R}^n$，我们使用如 (16) 中的指数平滑，并从 $\boldsymbol{p}_c^{(0)} = \boldsymbol{0}$ 开始。
$$ \boldsymbol{p}_{c}^{(g+1)} = (1 - c_{c})\boldsymbol{p}_{c}^{(g)} + \sqrt{c_{c}(2 - c_{c})\mu_{eff}} \frac{\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}}{c_{m}\sigma^{(g)}} \tag{24} $$
其中 * $\boldsymbol{p}_{c}^{(g)} \in \mathbb{R}^{n}$: 第 $g$ 代的进化路径。 * $c_{\rm c} \le 1$: 同样，$1/c_{\rm c}$ 是包含约 63% 总权重的进化路径 $\boldsymbol{p}_{\rm c}$ 的向后时间视界（比较 (20) 的推导）。$\sqrt{n}$ 和 $n$ 之间的时间视界是有效的。
因子 $\sqrt{c_{\rm c}(2-c_{\rm c})\mu_{\rm eff}}$ 是 $\boldsymbol{p}_{\rm c}$ 的归一化常数。对于 $c_{\rm c}=1$ 和 $\mu_{\rm eff}=1$，该因子减少为 1，且 $\boldsymbol{p}_{\rm c}^{(g+1)}=(\boldsymbol{x}_{1:\lambda}^{(g+1)}-\boldsymbol{m}^{(g)})/\sigma^{(g)}$。
因子 $\sqrt{c_{\mathrm{c}}(2-c_{\mathrm{c}})\mu_{\mathrm{eff}}}$ 的选择使得 $$ \boldsymbol{p}_c^{(g+1)} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \tag{25} $$ 如果 $$ \boldsymbol{p}_{c}^{(g)} \sim \frac{\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)}}{\sigma^{(g)}} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \quad \text{for all } i = 1, \dots, \mu \tag{26} $$
为了从 (26) 和 (24) 推导 (25)，请注意 $$ (1 - c_{\rm c})^2 + \sqrt{c_{\rm c}(2 - c_{\rm c})}^2 = 1 $$ 并且 $\sum_{i=1}^{\mu} w_i \mathcal{N}_i(\boldsymbol{0}, \boldsymbol{C}) \sim \frac{1}{\sqrt{\mu_{\rm eff}}} \mathcal{N}(\boldsymbol{0}, \boldsymbol{C})$ (27)
通过进化路径 $\boldsymbol{p}_c^{(g+1)}$ 更新协方差矩阵 $\boldsymbol{C}^{(g)}$ 的（rank-one）更新读作
$$ \boldsymbol{C}^{(g+1)} = (1 - c_1)\boldsymbol{C}^{(g)} + c_1 \boldsymbol{p}_c^{(g+1)} \boldsymbol{p}_c^{(g+1)^T} \tag{28} $$
(28) 中学习率的经验验证选择是 $c_1 \approx 2/n^2$。对于 $c_c = 1$ 和 $\mu = 1$，方程 (28), (22) 和 (16) 是相同的。
对于小的 $\mu_{\rm eff}$，使用进化路径更新 $\boldsymbol{C}$ 是对 (16) 的显著改进，因为连续步骤之间的相关性被大量利用。步骤的主导符号以及连续步骤之间的依赖关系对于结果进化路径 $\boldsymbol{p}_{\rm c}^{(g+1)}$ 起着重要作用。
我们考虑两种最极端的情况：完全相关步骤和完全反相关步骤。对于正相关，(24) 中的求和读作 $$ \sum_{i=0}^{g} (1 - c_{\rm c})^i \to \frac{1}{c_{\rm c}} \quad (\text{for } g \to \infty) $$
对于负相关， $$ \sum_{i=0}^{g} (-1)^{i} (1 - c_{c})^{i} \to \frac{c_{c}}{1 - (1 - c_{c})^{2}} = \frac{1}{2 - c_{c}} \quad (\text{for } g \to \infty) $$
将这些乘以应用于每个输入向量的 $\sqrt{c_c(2-c_c)}$，我们发现由于正相关，进化路径的长度被调制了高达 $$ \sqrt{\frac{2 - c_{\rm c}}{c_{\rm c}}} \approx \frac{1}{\sqrt{c_{\rm c}}} \tag{29} $$ 或者由于负相关，分别被其倒数调制。
使用 $\sqrt{n} \le 1/c_c \le n/2$，在雪茄状目标函数上适应几乎最优的协方差矩阵所需的函数评估次数变为 $\mathcal{O}(n)$，尽管学习率为 $c_1 \approx 2/n^2$。对此效应的一个合理解释是双重的。首先，所需的轴在路径中比在单个步骤中被（更）准确地表示。其次，学习率 $c_1$ 被调制：如 (29) 计算的进化路径长度的增加实际上类似于学习率增加了高达 $c_c^{-1/2}$ 倍。
最后一步，我们将 (16) 和 (28) 结合起来。
3.4 结合 Rank-$\mu$ 和 Rank-One 更新 (Combining Rank-$\mu$-Update and Cumulation)
协方差矩阵的最终 CMA 更新结合了 (16) 和 (28)。
$$ \boldsymbol{C}^{(g+1)} = \underbrace{(1 - c_1 - c_\mu \sum w_j)}_{\text{可以接近或等于 0}} \boldsymbol{C}^{(g)} + c_1 \underbrace{\boldsymbol{p}_{c}^{(g+1)} \boldsymbol{p}_{c}^{(g+1)^T}}_{\text{rank-one update}} + c_\mu \underbrace{\sum_{i=1}^{\lambda} w_i \, \boldsymbol{y}_{i:\lambda}^{(g+1)} \left(\boldsymbol{y}_{i:\lambda}^{(g+1)}\right)^T}_{\text{rank-}\mu \text{ update}} \tag{30} $$
其中 * $c_1 \approx 2/n^2$ * $c_\mu \approx \min(\mu_{\mathrm{eff}}/n^2, 1 - c_1)$ * $\boldsymbol{y}_{i:\lambda}^{(g+1)} = (\boldsymbol{x}_{i:\lambda}^{(g+1)} - \boldsymbol{m}^{(g)})/\sigma^{(g)}$ * $\sum w_j = \sum_{i=1}^{\lambda} w_i \approx -c_1/c_\mu$，但也参见附录 A 中的 (53) 和 (46)。
方程 (30) 对于 $c_1=0$ 简化为 (16)，对于 $c_\mu=0$ 简化为 (28)。该方程结合了 (16) 和 (28) 的优点。一方面，通过所谓的 Rank-$\mu$ 更新有效地使用了来自整个种群的信息。另一方面，通过将进化路径用于 Rank-One 更新，利用了代之间的相关性信息。前者在大种群中很重要，后者在小种群中特别重要。
4. 步长控制 (Step-Size Control)
上一节讨论的协方差矩阵自适应没有显式控制分布的“整体尺度”，即步长。协方差矩阵自适应仅在每个选中步骤的单个方向上增加或减少尺度——或者它通过一个给定的非自适应因子淡出旧信息来减少尺度。不那么非正式地说，除了 $\boldsymbol{C}^{(g)}$ 的自适应规则 (30) 之外，我们有两个具体的理由引入步长控制。
-
最优整体步长不能通过 (30) 很好地近似，特别是如果 $\mu_{\text{eff}}$ 选择大于 1。 例如，在 $f_{\text{sphere}}(\boldsymbol{x}) = \sum_{i=1}^{n} x_i^2$ 上，给定 $\boldsymbol{C}^{(g)} = \boldsymbol{I}$ 和 $\lambda \le n$，最优步长 $\sigma$ 大约等于 $\mu \sqrt{f_{\text{sphere}}(\boldsymbol{x})}/n$（对于相等重组权重）和 $1.25 \mu_{\text{eff}} \sqrt{f_{\text{sphere}}(\boldsymbol{x})}/n$（对于最优重组权重）。这种对 $\mu$ 或 $\mu_{\text{eff}}$ 的依赖性无法通过 (16) 或 (30) 实现。
-
(30) 中协方差矩阵更新的最大可靠学习率太慢，无法实现整体步长的竞争性变化率。 为了在 $f_{\text{sphere}}$ 上使用加权重组的进化策略实现最佳性能，整体步长必须在 $n$ 次函数评估内减少大约 $\exp(0.25) \approx 1.28$ 倍。也就是说，步长变化的时间视界必须与 $n$ 成正比或更短。从 (30) 中的学习率 $c_1$ 和 $c_\mu$ 可以得出，只要 $\mu_{\text{eff}} \ll n$，适应就太慢，无法在 $f_{\text{sphere}}$ 上表现出竞争力。这甚至可以通过模拟对于中等维度 $n \ge 10$ 和小 $\mu_{\text{eff}} \le 1 + \ln n$ 来验证。
为了控制步长 $\sigma^{(g)}$，我们利用进化路径，即连续步骤的总和（也见 3.3.2 节）。该方法可以独立于协方差矩阵更新应用，并表示为累积路径长度控制、累积步长控制或累积步长自适应 (CSA)。根据图 5 中描绘的推理，利用进化路径的长度。
- 每当进化路径短时，单步相互抵消（图 5，左）。粗略地说，它们是反相关的。如果步骤相互抵消，则应减小步长。
- 每当进化路径长时，单步指向相似的方向（图 5，右）。粗略地说，它们是相关的。因为步骤相似，所以同样的距离可以用更少但更长的步骤在相同方向上覆盖。在极限情况下，当连续步骤方向相同时，它们可以被任何扩大的单步替换。因此，应增加步长。
- 在期望的情况下，步骤在期望中是（大约）垂直的，因此不相关（图 5，中）。
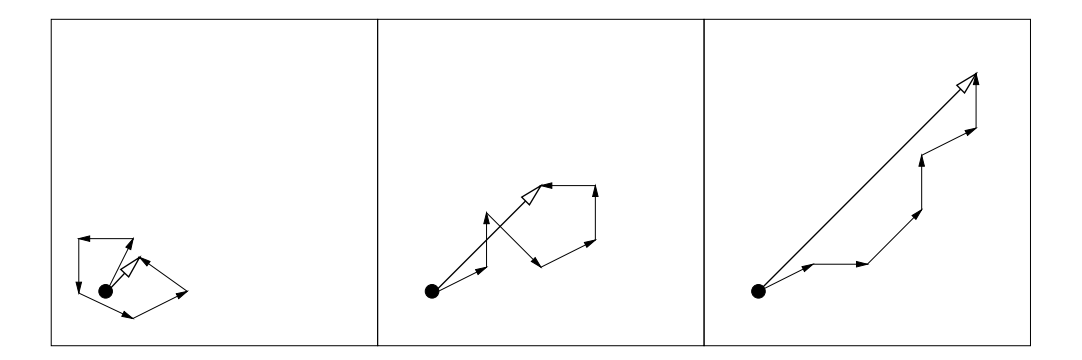图 5: 来自不同选择情况（理想化）的三个分别为六步的进化路径。单步的长度都具有可比性。进化路径（步骤总和）的长度显著不同，并被用于步长控制。
为了决定进化路径是“长”还是“短”，我们将路径的长度与其在随机选择下的期望长度进行比较，在随机选择下，连续步骤是独立的，因此是不相关的（不相关步骤是期望的情况）。如果选择偏差使进化路径比预期的长，则增加 $\sigma$，反之，如果选择偏差使进化路径比预期的短，则减小 $\sigma$。在理想情况下，选择不会使进化路径的长度产生偏差，其长度等于其在随机选择下的期望长度。
在实践中，为了构建进化路径 $\boldsymbol{p}_{\sigma}$，应用与 (24) 相同的技术。与 (24) 相比，构建的是共轭进化路径，因为来自 (24) 的进化路径 $\boldsymbol{p}_c$ 的期望长度取决于其方向（比较 (25)）。初始化为 $\boldsymbol{p}_{\sigma}^{(0)} = \boldsymbol{0}$，共轭进化路径读作
$$ \boldsymbol{p}_{\sigma}^{(g+1)} = (1 - c_{\sigma})\boldsymbol{p}_{\sigma}^{(g)} + \sqrt{c_{\sigma}(2 - c_{\sigma})\mu_{\text{eff}}} \boldsymbol{C}^{(g)^{-\frac{1}{2}}} \frac{\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}}{c_{\text{m}}\sigma^{(g)}} \tag{31} $$
其中 * $\boldsymbol{p}_{\sigma}^{(g)} \in \mathbb{R}^n$ 是第 $g$ 代的共轭进化路径。 * $c_{\sigma} < 1$。同样，$1/c_{\sigma}$ 是进化路径的向后时间视界（比较 (20)）。对于小 $\mu_{\text{eff}}$，$\sqrt{n}$ 和 $n$ 之间的时间视界是合理的。 * $\sqrt{c_{\sigma}(2-c_{\sigma})\mu_{\text{eff}}}$ 是归一化常数，见 (24)。 * $\boldsymbol{C}^{(g)^{-\frac{1}{2}}} \stackrel{\text{def}}{=} \boldsymbol{B}^{(g)} \boldsymbol{D}^{(g)^{-1}} \boldsymbol{B}^{(g)^{T}}$，其中 $\boldsymbol{C}^{(g)} = \boldsymbol{B}^{(g)} (\boldsymbol{D}^{(g)})^2 \boldsymbol{B}^{(g)^{T}}$ 是 $\boldsymbol{C}^{(g)}$ 的特征分解。
对于 $\boldsymbol{C}^{(g)} = \boldsymbol{I}$，我们有 $\boldsymbol{C}^{(g)^{-\frac{1}{2}}} = \boldsymbol{I}$ 且 (31) 复制了 (24)。变换 $\boldsymbol{C}^{(g)^{-\frac{1}{2}}}$ 在由 $\boldsymbol{B}^{(g)}$ 给出的坐标系中重新缩放步骤 $\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}$。
变换 $\boldsymbol{C}^{(g)^{-\frac{1}{2}}} = \boldsymbol{B}^{(g)}\boldsymbol{D}^{(g)^{-1}}\boldsymbol{B}^{(g)^{T}}$ 的单个因子可以解释如下（从右到左）： * $\boldsymbol{B}^{(g)^{T}}$ 旋转空间，使得 $\boldsymbol{B}^{(g)}$ 的列（即分布 $\mathcal{N}(\boldsymbol{0}, \boldsymbol{C}^{(g)})$ 的主轴）旋转到坐标轴中。结果向量的元素与相应特征向量上的投影有关。 * $\boldsymbol{D}^{(g)^{-1}}$ 应用（重新）缩放，使得所有轴变得同样大小。 * $\boldsymbol{B}^{(g)}$ 将结果旋转回原始坐标系。这个最后的变换确保分布的主轴不被整体变换旋转，且连续步骤的方向具有可比性。
因此，变换 $\boldsymbol{C}^{(g)^{-\frac{1}{2}}}$ 使得 $\boldsymbol{p}_{\sigma}^{(g+1)}$ 的期望长度独立于其方向，并且对于任何实现的协方差矩阵序列 $\boldsymbol{C}^{(g)}_{g=0,1,2,\dots}$，我们在随机选择下有 $\boldsymbol{p}_{\sigma}^{(g+1)} \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$，给定 $\boldsymbol{p}_{\sigma}^{(0)} \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$。
为了更新 $\sigma^{(g)}$，我们将 $\|\boldsymbol{p}_{\sigma}^{(g+1)}\|$ 与其期望长度 $E\|\mathcal{N}(\boldsymbol{0},\boldsymbol{I})\|$ 进行“比较”，即
$$ \ln \sigma^{(g+1)} = \ln \sigma^{(g)} + \frac{c_{\sigma}}{d_{\sigma}} \left( \frac{\|\boldsymbol{p}_{\sigma}^{(g+1)}\|}{E\|\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\|} - 1 \right) \tag{32} $$
其中 * $d_{\sigma} \approx 1$，阻尼参数，缩放 $\ln \sigma^{(g)}$ 的变化幅度。 * $E\|\mathcal{N}(\boldsymbol{0},\boldsymbol{I})\| = \sqrt{2}\,\Gamma(\frac{n+1}{2})/\Gamma(\frac{n}{2}) \approx \sqrt{n} + \mathcal{O}(1/n)$，$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$ 分布随机向量欧几里得范数的期望。
或者，我们可以使用平方范数 $\|\boldsymbol{p}_{\sigma}^{(g+1)}\|^2$ 在 (32) 中与期望值 $n$ 进行比较。在这种情况下，(32) 将读作
$$ \ln \sigma^{(g+1)} = \ln \sigma^{(g)} + \frac{c_{\sigma}}{2d_{\sigma}} \left( \frac{\|\boldsymbol{p}_{\sigma}^{(g+1)}\|^{2}}{n} - 1 \right) \tag{33} $$
步长变化在对数尺度上是无偏的，因为对于 $\boldsymbol{p}_\sigma^{(g+1)} \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$，有 $E[\ln\sigma^{(g+1)} \mid \sigma^{(g)}] = \ln\sigma^{(g)}$。方程 (31) 和 (32) 导致分布均值 $\boldsymbol{m}^{(g)}$ 的连续步骤大致为 $\boldsymbol{C}^{(g)}$-共轭。
为了证明连续步骤大致为 $\boldsymbol{C}^{(g)^{-1}}$-共轭，首先我们指出 (31) 和 (32) 适应 $\sigma$ 使得 $\boldsymbol{p}_{\sigma}^{(g+1)}$ 的长度大约等于 $E\|\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\|$。从 $(E\|\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\|)^2 \approx \|\boldsymbol{p}_{\sigma}^{(g+1)}\|^2 = \boldsymbol{p}_{\sigma}^{(g+1)^T} \boldsymbol{p}_{\sigma}^{(g+1)} = \text{RHS}^T \text{RHS of (31)}$ 开始，并假设 $\boldsymbol{C}^{(g)^{-1}} (\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)})$ 的期望平方长度不受选择改变（与其方向不同），我们得到
$$ \boldsymbol{p}_{\sigma}^{(g)^T} \boldsymbol{C}^{(g)^{-\frac{1}{2}}} (\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}) \approx 0 \tag{34} $$ 以及 $$ \left(\boldsymbol{C}^{(g)^{\frac{1}{2}}}\boldsymbol{p}_{\sigma}^{(g)}\right)^T \boldsymbol{C}^{(g)^{-1}}\left(\boldsymbol{m}^{(g+1)}-\boldsymbol{m}^{(g)}\right)\approx 0 \tag{35} $$
给定 $1/(c_1 + c_\mu) \gg 1$ 和 (34)，我们也假设 $\boldsymbol{p}_{\sigma}^{(g-1)^T} \boldsymbol{C}^{(g)^{-\frac{1}{2}}} (\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}) \approx 0$ 并推导
$$ \left(\boldsymbol{m}^{(g)} - \boldsymbol{m}^{(g-1)}\right)^T \boldsymbol{C}^{(g)^{-1}} \left(\boldsymbol{m}^{(g+1)} - \boldsymbol{m}^{(g)}\right) \approx 0 \tag{36} $$
也就是说，分布均值采取的步骤变得近似 $\boldsymbol{C}^{(g)^{-1}}$-共轭。
因为 $\sigma^{(g)} > 0$，(32) 等价于
$$ \sigma^{(g+1)} = \sigma^{(g)} \exp\left(\frac{c_{\sigma}}{d_{\sigma}} \left(\frac{\|\boldsymbol{p}_{\sigma}^{(g+1)}\|}{E\|\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\|} - 1\right)\right) \tag{37} $$
5. 讨论 (Discussion)
如果“经典”搜索方法，例如拟牛顿法 (BFGS) 和/或共轭梯度法，由于非凸或崎岖的搜索景观（例如尖锐的弯曲、不连续性、异常值、噪声和局部最优）而失败，CMA-ES 是非线性优化的一个有吸引力的选择。在 CMA-ES 中学习协方差矩阵类似于在拟牛顿法中学习逆 Hessian 矩阵。最终，任何凸二次（椭球）目标函数都被转换为球形函数 $f_{\text{sphere}}$。这可以在病态和/或不可分离的问题上将达到目标 $f$ 值所需的 $f$-评估次数减少几个数量级。
CMA-ES 克服了通常与进化算法相关的典型问题。 1. 在缩放不良和/或高度不可分离的目标函数上表现不佳。方程 (30) 使搜索分布适应缩放不良和不可分离的问题。 2. 使用大种群规模的内在需求。基于种群的搜索算法失败的一个典型但复杂的诊断原因是种群退化为子空间。这通常通过算法中的非自适应组件和/或大种群规模（比问题维度大得多）来防止。在 CMA-ES 中，种群规模可以自由选择，因为 (30) 中的学习率 $c_1$ 和 $c_\mu$ 甚至可以防止小种群规模（例如 $\lambda=9$）的退化。小种群规模通常导致更快的收敛，大种群规模有助于避免局部最优。 3. 种群的过早收敛。(37) 中的步长控制防止种群过早收敛。它并不阻止搜索最终陷入局部最优。
因此，CMA-ES 在大量测试函数上具有高度竞争力，并成功应用于许多现实世界问题。
最后，我们讨论在前面章节中应用的一些基本设计原则。
变化率 (Change rates) 我们将变化率定义为给定特定选择情况下每个采样搜索点的预期参数变化。为了在广泛的目标函数上实现具有竞争力的性能，需要仔细调整自适应参数的可能变化率。CMA-ES 分别控制分布均值 $\boldsymbol{m}$、协方差矩阵 $\boldsymbol{C}$ 和步长 $\sigma$ 的变化率。 * 均值 $\boldsymbol{m}$ 相对于给定样本分布的变化率由 $c_m$ 以及父代数量和重组权重决定。$\mu_{\text{eff}}$ 越大，$\boldsymbol{m}$ 的可能变化率越小。这对于大多数进化算法也是成立的。 * 协方差矩阵 $\boldsymbol{C}$ 的变化率由学习率 $c_1$ 和 $c_\mu$ 显式控制，因此与父代数量和种群规模分离。学习率反映了模型复杂度。在进化算法中，独立于种群规模和均值变化显式控制协方差的变化率是一个相当独特的特征。 * 步长 $\sigma$ 的变化率由阻尼参数 $d_\sigma$ 显式控制，并且特别独立于 $\boldsymbol{C}$ 的变化率。时间常数 $1/c_{\sigma} \le n$ 确保整体步长的变化足够快，特别是在小种群规模下。
不变性 (Invariance) 搜索算法的不变性属性表示在一组或一类目标函数上具有相同的行为。不变性是 CMA-ES 的一个重要属性。平移不变性在连续域优化中应被视为理所当然。平移不变性意味着在函数 $\boldsymbol{x} \mapsto f(\boldsymbol{x} + \boldsymbol{a})$，$\boldsymbol{x}^{(0)} = \boldsymbol{b} - \boldsymbol{a}$ 上的搜索行为独立于 $\boldsymbol{a} \in \mathbb{R}^n$。更多的不变性，例如对搜索空间某些线性变换的不变性，是非常可取的：它们意味着在函数类上具有统一的性能，因此允许推广经验结果。除了平移不变性外，CMA-ES 还表现出以下不变性： * 对目标函数值的保序（即严格单调）变换的不变性。算法仅取决于函数值的排名。 * 对搜索空间的保角（刚性）变换（旋转、反射和平移）的不变性，如果初始搜索点被相应地变换。 * 如果初始缩放，例如 $\sigma^{(0)}$，和初始搜索点 $\boldsymbol{m}^{(0)}$ 被相应地选择，则具有尺度不变性。 * 如果初始对角协方差矩阵 $\boldsymbol{C}^{(0)}$ 和初始搜索点 $\boldsymbol{m}^{(0)}$ 被相应地选择，则对变量的缩放具有不变性（对角不变性）。 * 对搜索空间的任何可逆线性变换 $\boldsymbol{A}$ 的不变性，如果初始协方差矩阵 $\boldsymbol{C}^{(0)} = \boldsymbol{A}^{-1} (\boldsymbol{A}^{-1})^T$，并且初始搜索点 $\boldsymbol{m}^{(0)}$ 被相应地变换。连同平移不变性，这也可以称为仿射不变性，即对仿射搜索空间变换的不变性。
不变性应是任何搜索算法的基本设计准则。连同有效适应不变性控制参数的能力，不变性是实现具有竞争力性能的关键。
平稳性或无偏性 (Stationarity or Unbiasedness) 随机搜索过程的一个重要设计准则是对象和策略参数变化的无偏性。考虑随机选择，例如目标函数 $f(\boldsymbol{x}) = r$ 且独立于 $\boldsymbol{x}$。如果其期望值在下一代保持不变，即 $E[\boldsymbol{m}^{(g+1)} \mid \boldsymbol{m}^{(g)}] = \boldsymbol{m}^{(g)}$，则种群均值是无偏的。对于种群均值，随机选择下的平稳性是一个相当直观的概念。在 CMA-ES 中，基本方程 (5) 中出现的所有参数都尊重平稳性。分布均值 $\boldsymbol{m}$、协方差矩阵 $\boldsymbol{C}$ 和 $\ln \sigma$ 是无偏的。$\ln \sigma$ 的无偏性并不意味着 $\sigma$ 是无偏的。在随机选择下，$E[\sigma^{(g+1)} \mid \sigma^{(g)}] > \sigma^{(g)}$，比较 (32)。
对于分布方差（或步长），每当选择压力低或未观察到改进时，增加或减少的偏见都会带来发散或过早收敛的风险。在有噪声的问题上，适当控制的增加偏见可能是合适的。它具有不可忽视的缺点，即终止的决定变得更加困难。
附录 A: 算法总结：The ($\mu/\mu_W, \lambda$)-CMA-ES
图 6 概述了完整的算法，总结了 (5), (9), (24), (30), (31), 和 (37)。按出现顺序使用的符号是：
- $\boldsymbol{y}_k \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{C})$，对于 $k = 1, \dots, \lambda$，是来自零均值和协方差矩阵 $\boldsymbol{C}$ 的多元正态分布的实现。
- $\boldsymbol{B}, \boldsymbol{D}$ 源于协方差矩阵 $\boldsymbol{C}$ 的特征分解，其中 $\boldsymbol{C} = \boldsymbol{B}\boldsymbol{D}^2\boldsymbol{B}^T$（参考 0.1 节）。$\boldsymbol{B}$ 的列是特征向量的正交基。对角矩阵 $\boldsymbol{D}$ 的对角元素是相应正特征值的平方根。虽然 (39) 肯定可以使用 $\boldsymbol{C}$ 的 Cholesky 分解来实现，但为了正确计算 (43) 和 (46) 中的 $\boldsymbol{C}^{-\frac{1}{2}} = \boldsymbol{B}\boldsymbol{D}^{-1}\boldsymbol{B}^T$，需要特征分解。
- $\boldsymbol{x}_k \in \mathbb{R}^n$，对于 $k = 1, ..., \lambda$。$\lambda$ 个搜索点的样本。
- $\langle \boldsymbol{y} \rangle_{w} = \sum_{i=1}^{\mu} w_{i} \boldsymbol{y}_{i:\lambda}$，忽略步长 $\sigma$ 的分布均值的步骤。
- $\boldsymbol{y}_{i:\lambda} = (\boldsymbol{x}_{i:\lambda} - \boldsymbol{m})/\sigma$，见下文 $\boldsymbol{x}_{i:\lambda}$。
- $\boldsymbol{x}_{i:\lambda} \in \mathbb{R}^n$，$\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{\lambda}$ 中第 $i$ 好的点。下标 $i:\lambda$ 表示第 $i$ 个排名的点的索引，即 $f(\boldsymbol{x}_{1:\lambda}) \le f(\boldsymbol{x}_{2:\lambda}) \le \dots \le f(\boldsymbol{x}_{\lambda:\lambda})$。
- $\mu = |\{w_i \mid w_i > 0\}| = \sum_{i=1}^{\lambda} \mathbb{1}_{(0,\infty)}(w_i) \ge 1$ 是严格正重组权重的数量。
- $\mu_{\text{eff}} = (\sum_{i=1}^{\mu} w_i^2)^{-1}$ 是方差有效选择质量，见 (8)。因为 $\sum_{i=1}^{\mu} |w_i| = 1$，我们有 $1 \le \mu_{\text{eff}} \le \mu$。
- $\boldsymbol{C}^{-\frac{1}{2}} \stackrel{\text{def}}{=} \boldsymbol{B} \boldsymbol{D}^{-1} \boldsymbol{B}^T$，见上文 $\boldsymbol{B}, \boldsymbol{D}$。通过反转对角元素可以求逆矩阵 $\boldsymbol{D}$。从定义中我们发现 $\boldsymbol{C}^{-\frac{1}{2}}\boldsymbol{y}_i = \boldsymbol{B}\boldsymbol{z}_i$，且 $\boldsymbol{C}^{-\frac{1}{2}}\langle \boldsymbol{y} \rangle_{_{\mathrm{W}}} = \boldsymbol{B} \sum_{i=1}^{\mu} w_i \, \boldsymbol{z}_{i:\lambda}$。
- $E\|\mathcal{N}(\boldsymbol{0},\boldsymbol{I})\| = \sqrt{2}\,\Gamma(\frac{n+1}{2})/\Gamma(\frac{n}{2}) \approx \sqrt{n}\,(1-\frac{1}{4n}+\frac{1}{21n^2})$。
- $h_{\sigma} = \begin{cases} 1 & \text{if } \frac{\|\boldsymbol{p}_{\sigma}\|}{\sqrt{1-(1-c_{\sigma})^{2(g+1)}}} < (1.4+\frac{2}{n+1})E\|\mathcal{N}(\boldsymbol{0},\boldsymbol{I})\| \\ 0 & \text{otherwise} \end{cases}$，其中 $g$ 是代数。Heaviside 函数 $h_{\sigma}$ 在 $\|\boldsymbol{p}_{\sigma}\|$ 很大时暂停 (45) 中 $\boldsymbol{p}_{c}$ 的更新。这防止了在线性环境中（即当步长太小时）$\boldsymbol{C}$ 的轴增加太快。当初始步长选择太小或目标函数随时间变化时，这是有用的。
- $\delta(h_{\sigma}) = (1 - h_{\sigma})c_{\rm c}(2 - c_{\rm c}) \le 1$ 相关性较小。在（不寻常的）$h_{\sigma} = 0$ 的情况下，它替代了 (47) 中来自 (45) 的第二个加项。
- $\sum w_i = \sum_{i=1}^{\lambda} w_i$ 是重组权重的总和，见 (49)–(53)。我们有 $-c_1/c_{\mu} \le \sum w_i \le 1$，且对于默认种群大小 $\lambda$，我们满足下界 $c_{\mu} \sum w_i = -c_1$。
设置参数
根据表 1 设置参数 $\lambda, w_{i=1...\lambda}, c_m, c_\sigma, d_\sigma, c_c, c_1, c_\mu$。
初始化
设置进化路径 $\boldsymbol{p}_{\sigma} = \boldsymbol{0}, \boldsymbol{p}_{c} = \boldsymbol{0}$，协方差矩阵 $\boldsymbol{C} = \boldsymbol{I}$，和 $g = 0$。 根据问题选择分布均值 $\boldsymbol{m} \in \mathbb{R}^n$ 和步长 $\sigma \in \mathbb{R}_{>0}$。
直到满足终止标准，g ← g + 1
采样新的搜索点群体，对于 $k = 1, \dots, \lambda$ $$ \boldsymbol{z}_k \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \tag{38} $$ $$ \boldsymbol{y}_k = \boldsymbol{B}\boldsymbol{D}\boldsymbol{z}_k \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{C}) \tag{39} $$ $$ \boldsymbol{x}_k = \boldsymbol{m} + \sigma \boldsymbol{y}_k \sim \mathcal{N}(\boldsymbol{m}, \sigma^2 \boldsymbol{C}) \tag{40} $$
选择与重组 $$ \langle \boldsymbol{y} \rangle_{\mathbf{w}} = \sum_{i=1}^{\mu} w_i \, \boldsymbol{y}_{i:\lambda} \quad \text{where } \sum_{i=1}^{\mu} w_i = 1, \ w_i > 0 \text{ for } i = 1 \dots \mu \tag{41} $$ $$ \boldsymbol{m} \leftarrow \boldsymbol{m} + c_{\mathrm{m}} \sigma \langle \boldsymbol{y} \rangle_{\mathrm{w}} \quad \text{equals } \sum_{i=1}^{\mu} w_{i} \, \boldsymbol{x}_{i:\lambda} \text{ if } c_{\mathrm{m}} = 1 \tag{42} $$
步长控制 $$ \boldsymbol{p}_{\sigma} \leftarrow (1 - c_{\sigma})\boldsymbol{p}_{\sigma} + \sqrt{c_{\sigma}(2 - c_{\sigma})\mu_{\text{eff}}} \boldsymbol{C}^{-\frac{1}{2}} \langle \boldsymbol{y} \rangle_{\text{w}} \tag{43} $$ $$ \sigma \leftarrow \sigma \times \exp\left(\frac{c_{\sigma}}{d_{\sigma}} \left(\frac{\|\boldsymbol{p}_{\sigma}\|}{E\|\mathcal{N}(\boldsymbol{0},\boldsymbol{I})\|} - 1\right)\right) \tag{44} $$
协方差矩阵自适应 $$ \boldsymbol{p}_{\rm c} \leftarrow (1 - c_{\rm c})\boldsymbol{p}_{\rm c} + h_{\sigma}\sqrt{c_{\rm c}(2 - c_{\rm c})\mu_{\rm eff}} \langle \boldsymbol{y} \rangle_{\rm w} \tag{45} $$ $$ w_i^{\circ} = w_i \times (1 \text{ if } w_i \ge 0 \text{ else } n/\|\boldsymbol{C}^{-\frac{1}{2}}\boldsymbol{y}_{i:\lambda}\|^2) \tag{46} $$ $$ \boldsymbol{C} \leftarrow (1 + c_1 \delta(h_{\sigma}) - c_1 - c_{\mu} \sum w_j) \boldsymbol{C} + c_1 \boldsymbol{p}_{c} \boldsymbol{p}_{c}^T + c_{\mu} \sum_{i=1}^{\lambda} w_i^{\circ} \boldsymbol{y}_{i:\lambda} \boldsymbol{y}_{i:\lambda}^T \tag{47} $$
图 6: The ($\mu/\mu_W, \lambda$)-CMA Evolution Strategy. 符号见正文
表 1: 默认参数 (2016)，其中 $\mu = \lfloor \lambda/2 \rfloor$，$\mu_{\rm eff} = \frac{(\sum_{i=1}^\mu w_i')^2}{\sum_{i=1}^\mu w_i'^2}$，$\mu_{\rm eff}^- = \frac{(\sum_{i=\mu+1}^\lambda w_i')^2}{\sum_{i=\mu+1}^\lambda w_i'^2}$。
选择与重组：
$$ \lambda = 4 + \lfloor 3 \ln n \rfloor \tag{48} $$ $$ w_i' = \ln \frac{\lambda + 1}{2} - \ln i \quad \text{for } i = 1, \dots, \lambda \tag{49} $$ $$ \alpha_{\mu}^{-} = 1 + c_1/c_{\mu} \tag{50} $$ $$ \alpha_{\mu_{\text{eff}}}^{-} = 1 + \frac{2\mu_{\text{eff}}^{-}}{\mu_{\text{eff}} + 2} \tag{51} $$ $$ \alpha_{\text{pos def}}^{-} = \frac{1 - c_1 - c_{\mu}}{n c_{\mu}} \tag{52} $$ $$ w_{i} = \begin{cases} \frac{1}{\sum |w'_{j}|^{+}} w'_{i} & \text{if } w'_{i} \ge 0 \\ \frac{\min(\alpha_{\mu}^{-}, \alpha_{\mu_{\text{eff}}}^{-}, \alpha_{\text{pos def}}^{-})}{\sum |w'_{j}|^{-}} w'_{i} & \text{if } w'_{i} < 0 \end{cases} \tag{53} $$ $$ c_{\rm m} = 1 \tag{54} $$
步长控制：
$$ c_{\sigma} = \frac{\mu_{\text{eff}} + 2}{n + \mu_{\text{eff}} + 5} $$ $$ d_{\sigma} = 1 + 2 \max\left(0, \sqrt{\frac{\mu_{\text{eff}} - 1}{n + 1}} - 1\right) + c_{\sigma} \tag{55} $$
协方差矩阵自适应：
$$ c_{\rm c} = \frac{4 + \mu_{\rm eff}/n}{n + 4 + 2\mu_{\rm eff}/n} \tag{56} $$ $$ c_1 = \frac{2}{(n+1.3)^2 + \mu_{\text{eff}}} \tag{57} $$ $$ c_{\mu} = \min\left(1 - c_1, 2 \frac{1/4 + \mu_{\text{eff}} + 1/\mu_{\text{eff}} - 2}{(n+2)^2 + \mu_{\text{eff}}}\right) \tag{58} $$
求解 $\sum |w_i|^-$ 得出 $$ \sum |w_i|^- < \frac{1 - c_1 - c_\mu}{(n - 1)c_\mu} \tag{60} $$
B. 实现关注点 (Implementational Concerns)
我们讨论一些实现问题。
B.1 多元正态分布
设向量 $\boldsymbol{z} \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$ 具有独立的 (0,1)-正态分布分量，可以在计算机上轻松采样。为了生成 (39) 的随机向量 $\boldsymbol{y} \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{C})$，我们设置 $\boldsymbol{y} = \boldsymbol{B}\boldsymbol{D}\boldsymbol{z}$（参见上文 $\boldsymbol{B}$ 和 $\boldsymbol{D}$ 的符号描述以及 0.1 和 0.2 节）。给定 $\boldsymbol{y}_k = \boldsymbol{B}\boldsymbol{D}\boldsymbol{z}_k$ 和 $\boldsymbol{C}^{-\frac{1}{2}} = \boldsymbol{B}\boldsymbol{D}^{-1}\boldsymbol{B}^T$，我们有 $\boldsymbol{C}^{-\frac{1}{2}}\langle\boldsymbol{y}\rangle_{\mathrm{w}} = \boldsymbol{B}\sum_{i=1}^{\mu}w_i\,\boldsymbol{z}_{i:\lambda}$（比较 (43)）。
B.2 策略内部数值计算量
在实践中，$\boldsymbol{B}$ 和 $\boldsymbol{D}$ 的重新计算直到大约 $\max(1, \lfloor 1/(10n(c_1+c_\mu))\rfloor)$ 代才需要进行。对于合理的 $c_1+c_\mu$ 值，这将由于特征分解引起的数值计算量从每个生成搜索点的 $\mathcal{O}(n^3)$ 减少到 $\mathcal{O}(n^2)$，即矩阵向量乘法的计算量。
注意，仅仅计算 $\boldsymbol{C}$ 的 Cholesky 分解是不够的，因为那样无法正确计算 (43)。
B.3 终止标准
一般而言，只要继续运行变成浪费 CPU 时间，最好重新启动（最终增加种群大小）或重新考虑编码和/或目标函数公式，算法就应该停止。我们推荐以下主要与数值稳定性相关的终止标准：
- NoEffectAxis: 如果在 $\boldsymbol{C}$ 的任何主轴方向上添加 0.1 倍标准差向量没有改变 $\boldsymbol{m}$，则停止。
- NoEffectCoord: 如果在任何单个坐标中添加 0.2 倍标准差没有改变 $\boldsymbol{m}$，则停止。
- ConditionCov: 如果协方差矩阵的条件数超过 $10^{14}$，则停止。
- EqualFunValues: 如果最后 $10 + \lceil 30n/\lambda \rceil$ 代的最佳目标函数值的范围为零，则停止。
- Stagnation: 我们跟踪最后 20% 但至少 $120 + 30n/\lambda$ 且不超过 20000 次迭代中的最佳和中位适应度的历史。如果在这两个历史中，最后（最近）30% 值的的中位数不比前 30% 的中位数好，则停止。
- TolXUp: 如果 $\sigma \times \max(\text{diag}(\boldsymbol{D}))$ 增加超过 $10^4$，则停止。这通常表明初始 $\sigma$ 太小，或发散行为。
应考虑两个其他有用的、依赖于问题的终止标准： * TolFun: 如果最后 $10+\lceil 30n/\lambda \rceil$ 代的最佳目标函数值和最近一代的所有函数值的范围低于 TolFun，则停止。选择 TolFun 取决于问题，而 $10^{-12}$ 是一个保守的初步猜测。 * TolX: 如果正态分布的标准差在所有坐标中都小于 TolX，并且 $\sigma \boldsymbol{p}^c$ 在所有分量中都小于 TolX，则停止。默认情况下，我们将 TolX 设置为初始 $\sigma$ 的 $10^{-12}$ 倍。
B.4 平坦适应度 (Flat fitness)
在种群中几个个体的函数值相等的情况下，增加步长是可行的（见下面源代码中的第 92-96 行）。这种方法可能会干扰终止标准 TolFun。在实践中，观察到平坦适应度应更像是一个终止标准，并导致重新考虑目标函数公式。
B.5 边界和约束
边界和约束的处理在一定程度上取决于问题。我们讨论一些原则和有用的方法。
最佳解严格在可行域内 如果最优解离不可行域不太近，处理任何类型的边界和约束的一种简单且充分的方法是： 1. 设置适应度为 $$ f_{\text{fitness}}(\boldsymbol{x}) = f_{\text{max}} + \|\boldsymbol{x} - \boldsymbol{x}_{\text{feasible}}\| \tag{62} $$ 其中 $f_{\text{max}}$ 大于可行种群或可行域（在最小化的情况下）中最差的适应度，$\boldsymbol{x}_{\text{feasible}}$ 是一个常数可行点，最好在可行域的中间。 2. 重新采样任何不可行解 $\boldsymbol{x}$ 直到它变得可行。
简单修复 可以在应用更新方程之前简单地修复不可行个体。这是不推荐的，因为 CMA-ES 对解点的分布做出了隐含假设，这种假设可能会被修复严重破坏。主要结果问题可能是发散或步长收敛太快。然而，对更改后的或注入的解进行（重新）修复以用于更新似乎可以解决发散问题（裁剪步长的马哈拉诺比斯距离以服从 $\|\boldsymbol{x} - \boldsymbol{m}\|_{\boldsymbol{C}}^2 / \sigma^2 \le n + 2n/(n + 2)$ 似乎就足够了）。注意，修复机制可能很难实现，特别是如果使用 $\boldsymbol{y}$ 或 $\boldsymbol{z}$ 在原始代码中实现更新方程。
惩罚 我们在修复后的搜索点 $\boldsymbol{x}_{\text{repaired}}$ 上评估目标函数，并根据与修复后解的距离添加惩罚。 $$ f_{\text{fitness}}(\boldsymbol{x}) = f(\boldsymbol{x}_{\text{repaired}}) + \alpha \|\boldsymbol{x} - \boldsymbol{x}_{\text{repaired}}\|^2 \tag{63} $$ 修复后的解随后被忽略。
在盒约束的情况下，$\boldsymbol{x}_{\text{repaired}}$ 被设置为与 $\boldsymbol{x}$ 距离最小的可行解。换句话说，$\boldsymbol{x}$ 中不可行的分量被设置为 $\boldsymbol{x}_{\text{repaired}}$ 中的（最近）边界值。
无修复机制可用 不可行搜索点 $\boldsymbol{x}$ 的适应度可以类似地计算为 $$ f_{\text{fitness}}(\boldsymbol{x}) = f_{\text{offset}} + \alpha \sum_{i} \mathbb{1}_{c_i > 0} \times c_i(\boldsymbol{x})^2 \tag{64} $$ 其中，不失一般性，（非线性）约束 $c_i: \mathbb{R}^n \to \mathbb{R}, \boldsymbol{x} \mapsto c_i(\boldsymbol{x})$ 在 $c_i(\boldsymbol{x}) \le 0$ 时满足，指示函数 $\mathbb{1}_{c_i > 0}$ 当 $c_i(\boldsymbol{x}) > 0$ 时为 1，否则为 0，$f_{\text{offset}} = \text{median}_k f(\boldsymbol{x}_k)$ 等于例如同一代中可行点的中位数或 25% 分位数或最佳函数值。如果没有其他信息可用，$c_i(\boldsymbol{x})$ 可以计算为 $\boldsymbol{x}$ 到种群中最佳或最近可行解或最近已知可行解的平方距离。后者让人想起上面的边界修复。
在 (63) 和 (64) 的任何一种情况下，$\alpha$ 的选择应使得 $f$ 的差异和第二个加项的差异具有相似的数量级。
C. MATLAB 源代码
此代码未实现负权重，即表 1 中对于 $i > \mu$，$w_i = 0$。
function xmin=purecmaes
% CMA-ES: Evolution Strategy with Covariance Matrix Adaptation for
% nonlinear function minimization.
% This code is an excerpt from cmaes.m and implements the key parts
% of the algorithm. It is intendend to be used for READING and
% UNDERSTANDING the basic flow and all details of the CMA *algorithm*.
% Computational efficiency is sometimes disregarded.
% ----- Initialization ------
% User defined input parameters (need to be edited)
strfitnessfct = 'felli'; % name of objective/fitness function
N = 10; % number of objective variables/problem dimension
xmean = rand(N,1); % objective variables initial point
sigma = 0.5; % coordinate wise standard deviation (step-size)
stopeval = 1e3*N^2; % stop after stopeval number of function evaluations
% Strategy parameter setting: Selection
lambda = 4+floor(3*log(N)); % population size, offspring number
mu = floor(lambda/2); % number of parents/points for recombination
weights = log(mu+1/2) - log(1:mu)'; % muXone array for weighted recombination
weights = weights/sum(weights); % normalize recombination weights array
mueff=sum(weights)^2/sum(weights.^2); % variance-effective size of mu
% Strategy parameter setting: Adaptation
cc = (4+mueff/N) / (N+4 + 2*mueff/N); % time constant for cumulation for C
cs = (mueff+2) / (N+mueff+5); % t-const for cumulation for sigma control
c1 = 2 / ((N+1.3)^2+mueff); % learning rate for rank-one update
cmu = min(1-c1, 2*(mueff-2+1/mueff) / ((N+2)^2+mueff)); % and for rank-mu update
damps = 1 + 2*max(0, sqrt((mueff-1)/(N+1))-1) + cs; % damping for sigma
% Initialize dynamic (internal) strategy parameters and constants
pc = zeros(N,1); ps = zeros(N,1); % evolution paths for C and sigma
B = eye(N,N); % B defines the coordinate system
D = ones(N,1); % diagonal D defines the scaling
C = B*diag(D.^2)*B'; % covariance matrix C
invsqrtC = B*diag(D.^-1)*B'; % C^-1/2
eigeneval = 0; % B and D updated at counteval == 0
chiN=N^0.5*(1-1/(4*N)+1/(21*N^2)); % expectation of ||N(0,I)|| == norm(randn(N,1))
% ----- Generation Loop -----
counteval = 0; % the next 40 lines contain the 20 lines of interesting code
while counteval < stopeval
% Generate and evaluate lambda offspring
for k=1:lambda,
arz(:,k) = randn(N,1); % standard normally distributed vector
arx(:,k) = xmean + sigma * (B * (D .* arz(:,k))); % add mutation
arfitness(k) = feval(strfitnessfct, arx(:,k)); % objective function call
counteval = counteval+1;
end
% Sort by fitness and compute weighted mean into xmean
[arfitness, arindex] = sort(arfitness); % minimization
xold = xmean;
xmean = arx(:,arindex(1:mu))*weights; % recombination, new mean value
% Cumulation: Update evolution paths
ps = (1-cs)*ps + sqrt(cs*(2-cs)*mueff) * invsqrtC * (xmean-xold) / sigma;
hsig = norm(ps)/sqrt(1-(1-cs)^(2*counteval/lambda))/chiN < 1.4+2/(N+1);
pc = (1-cc)*pc + hsig * sqrt(cc*(2-cc)*mueff) * (xmean-xold) / sigma;
% Adapt covariance matrix C
artmp = (1/sigma) * (arx(:,arindex(1:mu))-repmat(xold,1,mu));
C = (1-c1-cmu) * C ... % regard old matrix
+ c1 * (pc*pc' ... % plus rank one update
+ (1-hsig) * cc*(2-cc) * C) ... % minor correction if hsig==0
+ cmu * artmp * diag(weights) * artmp'; % plus rank mu update
% Adapt step-size sigma
sigma = sigma * exp((cs/damps)*(norm(ps)/chiN - 1));
% Update B and D from C
if counteval - eigeneval > lambda/(c1+cmu)/N/10 % to achieve O(N^2)
eigeneval = counteval;
C = triu(C) + triu(C,1)'; % enforce symmetry
[B,D] = eig(C); % eigen decomposition, B==normalized eigenvectors
D = sqrt(diag(D)); % D is a vector of standard deviations now
invsqrtC = B * diag(D.^-1) * B';
end
% Break, if fitness is good enough
if arfitness(1) <= 1e-10
break;
end
% Escape flat fitness, or better terminate?
if arfitness(1) == arfitness(ceil(0.7*lambda))
sigma = sigma * exp(0.2+cs/damps);
disp('warning: flat fitness, consider reformulating the objective');
end
disp([num2str(counteval) ': ' num2str(arfitness(1))]);
end % while, end generation loop
% ------ Final Message ------
disp([num2str(counteval) ': ' num2str(arfitness(1))]);
xmin = arx(:, arindex(1)); % Return best point of last generation.
% Notice that xmean is expected to be even
% better.
end
% -----
function f=felli(x)
N = size(x,1); if N < 2 error('dimension must be greater one'); end
f=1e6.^((0:N-1)/(N-1)) * x.^2; % condition number 1e6
end
D. 学习参数的重构 (Reformulation of Learning Parameter $c_{cov}$)
为了保持一致性和清晰度，我们重新制定了 (47) 中的学习系数，并替换
$$ \frac{c_{\text{cov}}}{\mu_{\text{cov}}} \quad \text{with} \quad c_1 \tag{65} $$
$$ c_{\text{cov}} \left( 1 - \frac{1}{\mu_{\text{cov}}} \right) \quad \text{with} \quad c_{\mu} \tag{66} $$
$$ 1 - c_{\text{cov}} \quad \text{with} \quad 1 - c_1 - c_{\mu} \tag{67} $$
并选择（在 (57) 和 (58) 中）
$$ c_1 = \frac{2}{(n+1.3)^2 + \mu_{\text{cov}}} \tag{68} $$
$$ c_{\mu} = \min \left( 2 \frac{\mu_{\text{cov}} - 2 + \frac{1}{\mu_{\text{cov}}}}{(n+2)^2 + \mu_{\text{cov}}}, 1 - c_1 \right) \tag{69} $$
得到的系数与之前的非常相似。与以前的公式相比，$c_1$ 在 $\mu_{\text{eff}}^{-1}$ 中变得单调，而 $c_1 + c_\mu$ 在 $\mu_{\text{eff}}$ 中变得几乎单调。
另一种仅取决于协方差矩阵自由度并额外校正非常小 $\lambda$ 的替代方案读作
$$ c_1 = \frac{\min(1, \lambda/6)}{m + 2\sqrt{m} + \frac{\mu_{\text{eff}}}{n}} \tag{70} $$
$$ c_{\mu} = \min \left( 1 - c_1, \frac{\alpha_{\mu}^0 + \mu_{\text{eff}} - 2 + \frac{1}{\mu_{\text{eff}}}}{m + 4\sqrt{m} + \frac{\mu_{\text{eff}}}{2}} \right) \tag{71} $$
$$ \alpha_{\mu}^{0} = 0.3 \tag{72} $$
其中 $m=\frac{n^2+n}{2}$ 是协方差矩阵中的自由度。对于 $\mu_{\rm eff}=1$，系数 $c_\mu$ 现在被选择为大于零，因为 $\alpha_\mu^0>0$。图 8 比较了新的学习率与旧的学习率。
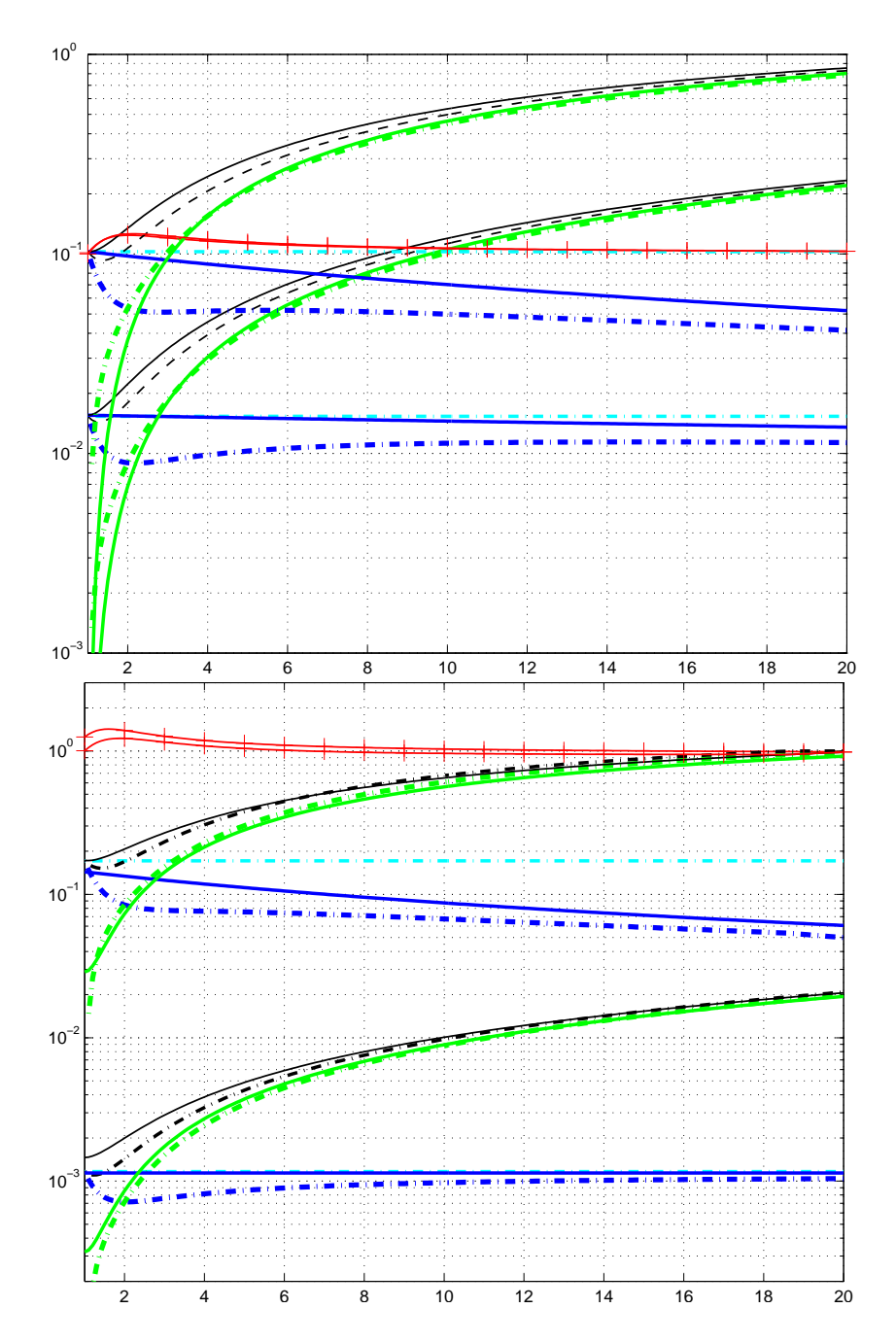图 8: 学习率 $c_1, c_\mu$（实线）和 $c_{\rm cov}$（点划线）随 $\mu_{\rm eff}$ 的变化。上方：方程 (68) 等，对于 n=3;10。下方：方程 (70) 等，对于 n=2;40。