2. The Basics

2.1 Evolutionary Algorithms

Evolutionary Algorithms 是受自然选择启发的算法。其大概的流程是：在每一次迭代中，根据fitness，从群体中选出较好的个体生成/繁殖下一代，较差的个体被丢弃，直到达到终止条件。

以下是几个基本的概念。

2.1.1 Representation

EA 里面使用的个体需要一种特定的表示，来进行selection, crossover, mutation等进化算子。主要是将你要求解的问题domain转化为使用数字表示的“染色体”。

主要有两种representation：直接编码和间接编码。

直接编码： 基因型和表型一一对应，比如每一个权重都对应到基因型的一个数字。

间接编码： 基因型定义一系列如生成规则的东西，将基因型逐渐生成表型。

2.1.2 Population-Based Search

2.1.3 Selection

也就是从群体中挑选个体进行下一轮繁殖的过程。fitness小的个体被丢弃的概率如果比较高，那么就会导致收敛过快。反之，会导致收敛变慢，但是会更倾向于探索。

2.1.4 Variation Operators

也就是如何去变异个体。

2.1.5 Fitness Evalution

对个体的评估，相当于一个零阶信息，没有导数信号。

2.1.6 Reproduction and Replacement

2.1.7 Termination

2.2 Types of Evolutionary Algorithms

下面介绍几个基本的EA算法。

2.2.1 Genetic Algorithms

GA的selection有以下几种：

• Roulette Wheel Selection: Individuals are selected probabilistically based on their fitness, with better individuals having a higher chance of being chosen.
• Tournament Selection: A small group of individuals is selected randomly, and the fittest individual in the group is chosen.
• Rank-Based Selection: Individuals are ranked based on their fitness, and selection probabilities are assigned according to their rank.
• Truncation Selection: This method involves selecting the top fraction of individuals based solely on their fitness. Only the highest-performing individuals above a certain fitness threshold contribute to the next generation, while the rest are excluded. Truncation selection often leads to rapid convergence but can reduce genetic diversity.

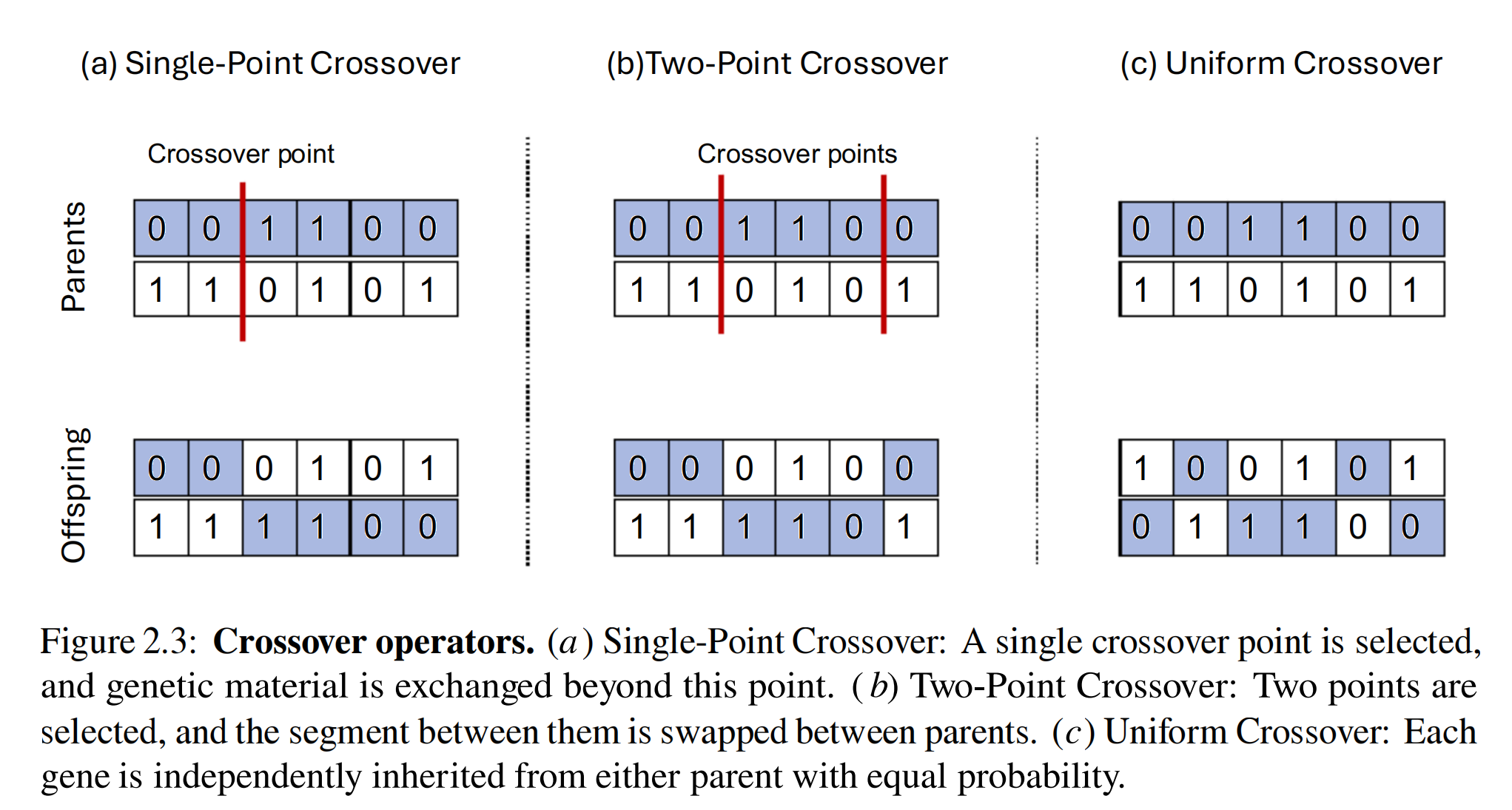
接下来是GA的Reproduction方法，分为Single-Point Crossover, Two-Point Crossover, Uniform Crossover。具体无需多言，直接上图：

2.2.2 Evolution Strategy

ES表示个体的方法主要是一组实数。

有两个Selection：$(\mu, \lambda)$-ES 和$(\mu + \lambda)$-ES。通常$\mu \le \lambda$。

• $(\mu, \lambda)$-ES: 先使用 $\mu $ 个parents生成 $ \lambda $ 个offspring，然后从 $\lambda$ 个offspring中选 $\mu$ 个作为下一代(Parents are not considered）。

• $(\mu + \lambda)$-ES: 先使用 $\mu $ 个parents生成 $ \lambda $ 个offspring，然后从 $\mu$ 个parents和 $\lambda$ 个offspring中选 $\mu$ 个作为下一代。

Variation主要是通过mutation来实现的。也就是给每个个体加上高斯噪声。

2.2.3 Covariance-Matrix Adaptation Evolution Strategy

前面介绍的两个方法有一个通病：方差是固定不变的。

但是，有时我们需要探索的更大胆，有时我们需要探索的更小心。

CMA-ES就是为了解决这个问题而设计的。主要步骤如下：

只关注当前代中表现最好的 $N_{best}$ 个解（例如前 25%）。每一轮中进行操作：

更新均值：下一代的均值 $\mu^{(g+1)}$ 仅由当前代最好的 $N_{best}$ 个解计算得出：
$$ \mu^{(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} x $$

更新协方差：在估算下一代的协方差矩阵 $C^{(g+1)}$ 时，关键技巧是使用当前代的均值 $\mu^{(g)}$，而不是刚刚计算出的新均值 $\mu^{(g+1)}$。这有助于捕捉搜索方向的动量：
$$ \sigma_x^{2,(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} (x_i - \mu_x^{(g)})^2 $$
$$ \sigma_y^{2,(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} (y_i - \mu_y^{(g)})^2 $$
$$ \sigma_{xy}^{(g+1)} = \frac{1}{N_{best}} \sum_{i=1}^{N_{best}} (x_i - \mu_x^{(g)})(y_i - \mu_y^{(g)}) $$

利用这些更新后的均值$\mu^{(g+1)}$，协方差矩阵 $C^{(g+1)}$，我们可以从新的多变量正态分布 $N(\mu^{(g+1)}, C^{(g+1)})$ 中采样下一代候选解。

2.2.4 OpenAI Evolution Strategy

NES 的核心思想是最大化适应度分数的期望值。它利用整个种群的信息（包括表现差的个体）来估计梯度，并使用梯度下降来更新分布参数 $\theta$。

目标函数

定义目标函数 $J(\theta)$ 为适应度函数 $F(z)$ 在参数为 $\theta$ 的概率分布 $\pi(z, \theta)$ 下的期望值：
$$ J(\theta) = E_{\theta}[F(z)] = \int F(z) \,\pi(z, \theta) \,dz $$

梯度估计

使用对数似然技巧，我们可以推导出 $J(\theta)$ 关于 $\theta$ 的梯度：
$$ \nabla_{\theta} J(\theta) = E_{\theta} [F(z) \nabla_{\theta} \log \pi(z, \theta)] $$
在大小为 $N$ 的种群中，可以通过求和来近似这个梯度：
$$ \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} F(z^{i}) \nabla_{\theta} \log \pi(z^{i}, \theta) $$

参数更新

有了梯度估计，我们就可以使用学习率 $\alpha$ 来更新参数 $\theta$：
$$ \theta \to \theta + \alpha \nabla_{\theta} J(\theta) $$

特例：多变量正态分布

如果 $\pi(z, \theta)$ 是分解的多变量正态分布（即无相关性），参数 $\theta$ 包含 $\mu$ 和 $\sigma$。对于种群中的每个解 $i$ 和每个参数维度 $j$，梯度的闭式解为：
$$ \nabla_{\mu_{j}} \log N(z^{i}, \mu, \sigma) = \frac{z_{j}^{i} - \mu_{j}}{\sigma_{i}^{2}} $$
$$ \nabla_{\sigma_{j}} \log N(z^{i}, \mu, \sigma) = \frac{(z_{j}^{i} - \mu_{j})^{2} - \sigma_{j}^{2}}{\sigma_{i}^{3}} $$
这些公式被用于更新 $\mu$ 和 $\sigma$，使得种群分布向高适应度区域移动，并根据需要收缩或扩大搜索范围（$\sigma$）。

OpenAI ES 是 NES 的一个特例，它固定了标准差 $\sigma$，仅更新均值 $\mu$。这简化了算法，并使其非常适合大规模并行计算。

2.2.5 Multiobjective Evolutionary Algorithms

也就是多个目标同时优化。

Pareto-optimal solution: 一个解是Pareto-optimal的，如果它没有被其他解支配。也就是说，如果不存在一个解在所有目标上都比当前这个解好，那么这个解就是Pareto-optimal的。

EA天生就十分适合这种问题。

2.2.6 Further Evolutionary Computation Techniques

略