Evolution Strategies as a Scalable Alternative to Reinforcement Learning

作者: Tim Salimans, Jonathan Ho, Xi Chen, Szymon Sidor, Ilya Sutskever (OpenAI)

论文链接: http://arxiv.org/abs/1703.03864v2

日期：2017年9月7日

被引用：2111（来自谷歌学术）

写在前面

这是Evolution Strategies方法中十分经典的一篇论文，也是被Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning引用了不少次。希望以后可以精读。

这是一个在线阅读的网站：https://openai.com/index/evolution-strategies/

引言

强化学习算法主要用两种，一种是基于MDP的，也是目前最为主流的，另一种是使用所谓的黑盒优化策略。本文就是尝试使用黑盒优化策略Evolution Strategies。本文的主要发现作者列出有以下几点：

1. 本文提出的Virtual Batch Normalization在ES中十分重要，同时神经网络策略的重参数化也可以很好的提升性能。
2. 使用本文使用的所谓“公共随机数方法可以让ES实现高度并行化。
3. ES所需要使用的数据比A3C要多，但是由于ES不需要反向传播和价值函数，计算量和达到同样效果的时间比A3C要少。
4. ES的探索行为比TRPO之类的算法要好，可以理解为ES探索未知的能力更强。
5. ES的鲁棒性比较好，体现在ES使用的超参数在同样的任务上一致。

方法

ES

$\theta$ 是当前策略网络的参数。我们给它加上噪声，并定义目标函数如下

$$ J(\theta) = \mathbb{E}_{\theta \sim p_{\psi}} F(\theta) = \mathbb{E}_{\epsilon \sim N(0,I)} F(\theta + \sigma \epsilon) $$

标准差$\sigma$是超参数。

设 $\tilde{\theta} = \theta + \sigma \epsilon$，则 $\tilde{\theta} \sim N(\theta, \sigma^2 I)$。其概率密度函数为：
$$ p(\tilde{\theta}; \theta) = \frac{1}{(2\pi)^{d/2}\sigma^d} \exp\left(-\frac{1}{2\sigma^2}\|\tilde{\theta} - \theta\|^2\right) $$

$$ \nabla_\theta \log p(\tilde{\theta}; \theta) = \frac{1}{\sigma^2}(\tilde{\theta} - \theta) = \frac{1}{\sigma^2}(\sigma \epsilon) = \frac{\epsilon}{\sigma} $$

于是我们有
$$ \begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta \int F(\tilde{\theta}) p(\tilde{\theta}; \theta) d\tilde{\theta} \\ &= \int F(\tilde{\theta}) \nabla_\theta p(\tilde{\theta}; \theta) d\tilde{\theta} \\ &= \int F(\tilde{\theta}) p(\tilde{\theta}; \theta) \nabla_\theta \log p(\tilde{\theta}; \theta) d\tilde{\theta} \\ &= \mathbb{E}_{\tilde{\theta} \sim p(\cdot; \theta)} [F(\tilde{\theta}) \nabla_\theta \log p(\tilde{\theta}; \theta)] \\ &= \mathbb{E}_{\epsilon \sim N(0, I)} \left[ F(\theta + \sigma \epsilon) \frac{\epsilon}{\sigma} \right] \end{aligned} $$

最后有
$$ \boxed{ \nabla_{\theta} \mathbb{E}_{\epsilon \sim N(0,I)} F(\theta + \sigma \epsilon) = \frac{1}{\sigma} \mathbb{E}_{\epsilon \sim N(0,I)} \{ F(\theta + \sigma \epsilon) \epsilon \} } $$

这就是我们目标函数的梯度，也是我们更新参数$\theta$的依据。

在实践中，我们可以通过采样去近似期望 $\mathbb{E}_{\epsilon \sim N(0,I)}$。

1. 采样 $n$ 个噪声向量 $\epsilon_1, \dots, \epsilon_n \sim N(0, I)$
2. 计算每个扰动参数的回报 $F_i = F(\theta_t + \sigma \epsilon_i)$
3. 更新参数$$\theta_{t+1} \leftarrow \theta_t + \alpha \frac{1}{\sigma} \frac{\sum_{i=1}^n F_i \epsilon_i}{n}$$

并行

episode在强化学习中指智能体从初始状态开始，与环境持续交互直到达到终止条件（如游戏结束、死亡或达到最大步数）的一个完整过程。

由于黑盒优化是完成了整个episode之后更新参数，所以并行化十分容易，我们只要让所有worker共享一个随机数列表，来指导生成噪声，然后相互传递交流一个参数对应的适应度/回报即可。ES 的优化目标正是最大化整个 Episode 的累积回报。

也就是每个时间步，每个 Worker $i$并行执行以下操作：

1. 从公共种子生成扰动 $\epsilon_i \sim \mathcal{N}(0, I)$.
2. 计算回报 $F_i = F(\theta_t + \sigma \epsilon_i)$.
3. 广播标量 $F_i$ 给所有其他 Worker.
4. 接收所有 $\{F_j\}_{j=1}^N$.
5. 利用种子重构所有 $\{\epsilon_j\}_{j=1}^N$.
6. $$\theta_{t+1} \leftarrow \theta_t + \alpha \frac{1}{\sigma} \frac{\sum_{i=1}^n F_i \epsilon_i}{n}$$

Virtual Batch Normalization

在将 ES 应用于深度神经网络（特别是处理像素输入的 CNN）时，作者发现直接对参数加高斯噪声往往导致探索失败。常见的现象是策略“坍缩”：无论输入什么画面，策略都输出完全相同的动作。这是因为深层网络的参数对输出分布的影响非常敏感且非线性。

为了解决这个问题，论文引入了 VBN。

1. 在训练开始前，收集并固定一批具有代表性的观测数据 $X_{ref}$。
2. 计算 $X_{ref}$ 的均值 $\mu_{ref}$ 和标准差 $\sigma_{ref}$，并在整个训练过程中保持不变。
3. 对任意输入 $x$，使用固定的 $\mu_{ref}$ 和 $\sigma_{ref}$ 进行归一化：
   $$ \hat{x} = \frac{x - \mu_{ref}}{\sigma_{ref}} $$
   随后接标准的缩放和平移变换 $y = \gamma \hat{x} + \beta$。

讨论

噪声的类比

文中提出了一个Policy Gradients (PG) 和 Evolution Strategies (ES) 的一个有意思的噪声的类比。

Policy Gradients (PG)：在动作空间 添加噪声。

PG 通过从一个分布（如 Softmax 或 高斯分布）中采样动作来实现这一点。
目标函数为 $F_{PG}(\theta) = \mathbb{E}_{\epsilon} R(\mathbf{a}(\epsilon, \theta))$。其梯度为：

$$ \nabla_{\theta} F_{PG}(\theta) = \mathbb{E}_{\epsilon} \{ R(\mathbf{a}(\epsilon, \theta)) \nabla_{\theta} \log p(\mathbf{a}(\epsilon, \theta); \theta) \} $$

Evolution Strategies (ES)：在参数空间 添加噪声。

ES 对参数进行扰动 $\tilde{\theta} = \theta + \sigma \epsilon$，然后基于扰动后的参数确定性地执行动作。这相当于对原始目标函数进行“高斯模糊”平滑。目标函数为 $F_{ES}(\theta) = \mathbb{E}_{\epsilon} R(\mathbf{a}(\epsilon, \theta))$。其梯度为：

$$ \nabla_{\theta} F_{ES}(\theta) = \mathbb{E}_{\epsilon} \{ R(\mathbf{a}(\epsilon, \theta)) \nabla_{\theta} \log p(\tilde{\theta}(\epsilon, \theta); \theta) \} $$

尽管两种方法看似相似（都是引入噪声来平滑目标），但噪声引入的位置决定了它们在方差特性上的巨大差异。

ES 和 Policy Gradients（PG）

我们考虑两者的方差

$$ \begin{aligned} \operatorname{Var}[\nabla_{\theta} F_{PG}(\theta)] &\approx \operatorname{Var}[R(\mathbf{a})] \operatorname{Var}[\nabla_{\theta} \log p(\mathbf{a}; \theta)] \\ \operatorname{Var}[\nabla_{\theta} F_{ES}(\theta)] &\approx \operatorname{Var}[R(\mathbf{a})] \operatorname{Var}[\nabla_{\theta} \log p(\tilde{\theta}; \theta)] \end{aligned} $$

如果两种方法进行相似程度的探索，$\operatorname{Var}[R(\mathbf{a})]$ 项是相似的。关键差异在于第二项：

$\nabla_{\theta} \log p(\mathbf{a}; \theta) = \sum_{t=1}^{T} \nabla_{\theta} \log p(a_t; \theta)$ 是 $T$ 个不相关项的和。因此，PG 梯度估计的方差会随着时间步 $T$ 线性增长。为了降低方差，PG 通常引入折扣因子 或价值函数 。但这会带来偏差，特别是在动作具有长期影响的情况下。

$\nabla_{\theta} \log p(\tilde{\theta}; \theta)$ 与时间步 $T$ 无关。同时 ES 不需要引入折扣因子或价值函数近似。

Problem Dimensionality

由于

$$\mathbb{E}_{\epsilon \sim N(0,I)} \left[ \frac{F(\theta)}{\sigma} \epsilon \right] = 0 $$

所以

$$\nabla_{\theta} F(\theta) = \mathbb{E}_{\epsilon \sim N(0,I)} \left[ \frac{F(\theta + \sigma \epsilon) - F(\theta)}{\sigma} \epsilon \right] $$

所以 ES 的梯度估计本质上可以看作是高维空间中的随机有限差分。

传统优化理论（如 Nesterov & Spokoiny, 2011）指出，对于一般的非光滑优化问题，所需的优化步数通常与参数维度呈线性关系。也就是ES本质上并没有提升速率。

但在本文中，作者提出了一个深刻的观点：优化的难度取决于问题的intrinsic dimension，而不是参数的表面维度。 即使参数量巨大，并不意味着优化问题本身变得更难了。

线性模型的例子：考虑一个线性模型 $\hat{y} = \mathbf{x} \cdot \mathbf{w}$。如果我们把输入特征 $\mathbf{x}$ 复制一遍拼成 $(\mathbf{x}, \mathbf{x})$，参数 $\mathbf{w}$ 也随之翻倍。虽然参数量加倍了，但数学本质没变。只要将 ES 的学习率和噪声标准差进行适当调整（除以 $\sqrt{2}$ 或 2），ES 的表现将完全一致。这说明只要参数存在冗余，维度的增加不会拖慢 ES。

作者也做了一些实验去证明这一点。

实验

MuJoCo

与 TRPO (Trust Region Policy Optimization) 进行对比。
* ES 能够解决所有测试的 MuJoCo 任务，达到与 TRPO 相当的最终性能。
* 数据效率：在简单任务上 ES 甚至比 TRPO 更快；在困难任务（如 Humanoid）上，ES 需要的数据量大约是 TRPO 的 10 倍。但考虑到 ES 可以大规模并行，其实际训练时间可能更短。

Atari

在 51 个 Atari 游戏上测试 ES，训练 10 亿帧。
* 训练时间：使用 720 个 CPU 核，仅需 1 小时 即可完成训练（对比 A3C 需要 1 天）。
* 性能：在 23 个游戏中优于 A3C，28 个游戏中差于 A3C。

并行化

这是本文最震撼的实验结果之一。在 3D Humanoid 任务上测试了 ES 的扩展能力。

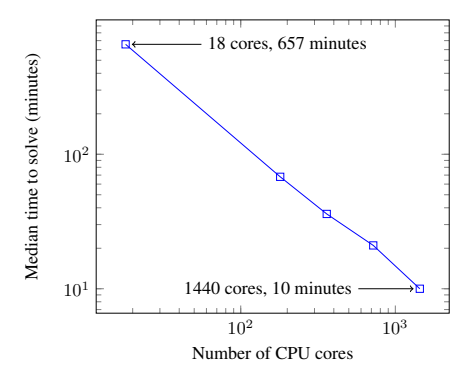
• 图 1：达到目标分数所需的时间随 CPU 核心数的变化。
• 结论：ES 展现了完美的线性加速。使用 1440 个核心，可以在 10 分钟 内解决 3D Humanoid 任务（单机通常需要 11 小时）。这证明了 ES 极低的通信开销使得大规模分布式训练成为可能。

对时间分辨率的不变性

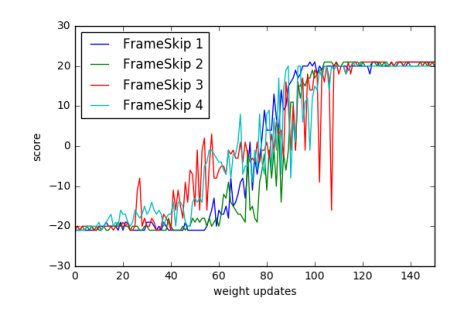
• 图 2：在 Pong 游戏中，改变 Frame-skip 参数（{1, 2, 3, 4}）。
• 结论：学习曲线几乎重合。这证明 ES 不像传统 RL 那样依赖精细调整的 Frame-skip 参数，具有更好的鲁棒性。

结论

本文展示了进化策略 (ES) 是深度强化学习的一种强有力的竞争算法。

• 优势总结：
  1. 可扩展性：基于公共随机数的通信策略使得 ES 可以扩展到数千 CPU，实现线性加速。
  2. 简单性：无需反向传播，无需价值函数，代码实现简单。
  3. 鲁棒性：对稀疏奖励、长视界、动作频率不敏感。
• 展望：ES 特别适合元学习 (Meta-learning)、低精度硬件加速以及那些传统 MDP 方法难以处理的复杂奖励结构问题。