Multi-scale Evolutionary Neural Architecture Search for Deep Spiking Neural Networks
深度脉冲神经网络的脑启发多尺度演化神经架构搜索
原文链接: http://arxiv.org/abs/2304.10749v5
作者: Wenxuan Pan, Feifei Zhao, Guobin Shen, Bing Han, Yi Zeng (中科院自动化所)
摘要 (Abstract)
脉冲神经网络(SNN)因其离散信号处理带来的能源效率以及整合多尺度生物可塑性的潜力而备受关注。然而,大多数 SNN 直接采用深度神经网络(DNN)的结构,很少针对 SNN 进行自动化的神经架构搜索(NAS)。
人脑具有微观(神经元)、介观(神经回路模体)和宏观(脑区连接)的多尺度拓扑结构,这是自然进化的产物。受此启发,本文提出了多尺度演化神经架构搜索(MSE-NAS):
1. 搜索空间:同时考虑微观、介观和宏观尺度的脑拓扑结构。
2. 演化对象:演化单个神经元操作、多个电路模体(Motifs)的自组织整合以及模体间的全局连接。
3. 评估方法:提出了一种脑启发的间接评估(BIE)函数,无需训练即可评估适应度,极大地减少了计算消耗。
实验表明,MSE-NAS 在静态数据集(CIFAR10/100)和神经形态数据集(CIFAR10-DVS, DVS128-Gesture)上均实现了 SOTA 性能,且具有极佳的迁移性、鲁棒性和能源效率。
核心机制详解:卷积与脉冲神经元的结合
针对你关于“卷积与神经元如何结合”以及“模型如何训练”的疑问,这里进行详细的数学化解释。
1. 卷积与 LIF 神经元的结合 (Conv-LIF Dynamics)
在深度脉冲神经网络(Deep SNN)中,卷积层充当了突触(Synapse)的角色,负责对输入脉冲进行加权求和,而 LIF 神经元充当了非线性激活函数(Activation)的角色,负责积分和发放脉冲。
这一过程可以描述为:$Input \ Spikes \xrightarrow{Conv} Current \xrightarrow{LIF} Output \ Spikes$。
(1) 突触积分 (Synaptic Integration via Convolution)
假设第 $l$ 层的输入是脉冲张量 $S^{(l-1)}(t)$,其中 $t$ 是时间步。卷积操作 $W$ 作用于输入脉冲,产生注入神经元的电流 $I(t)$:
$$ I^{(l)}(t) = W^{(l)} \circledast S^{(l-1)}(t) $$
这里 $\circledast$ 代表卷积操作。在 MSE-NAS 中,微观尺度(Micro)的进化就是在选择这个 $W$ 的核大小($3\times3$ 或 $5\times5$)。
(2) 神经元动力学 (Neuronal Dynamics)
每个神经元维护一个膜电位 $V(t)$。本文采用 Leaky Integrate-and-Fire (LIF) 模型。
连续时间微分方程:
$$
\tau_m \frac{dV_m(t)}{dt} = I(t) - V_m(t) \tag{1}
$$
离散时间差分方程(实际计算机实现):
在时间步 $t$,膜电位 $V[t]$ 的更新包含两部分:上一时刻的电压衰减泄漏(Leaky)和当前时刻输入电流的积分(Integrate)。
$$ V[t] = \left(1 - \frac{1}{\tau_m}\right) V[t-1] + I[t] $$
(3) 脉冲发放与重置 (Fire and Reset)
当膜电位超过阈值 $V_{th}$(文中设为 0.5)时,神经元发放脉冲 $S[t]$,并将膜电位重置(通常重置为0或减去阈值):
$$ S[t] = \begin{cases} 1, & \text{if } V[t] \geq V_{th} \\ 0, & \text{otherwise} \end{cases} $$
$$ V[t] \leftarrow V[t] \cdot (1 - S[t]) \quad \text{(Hard Reset)} $$
通过这种方式,卷积负责空间特征提取,LIF 神经元负责时域信息的累积与非线性变换,二者结合构成了 SNN 的基本计算单元。
2. 模型的训练方法 (Training Strategy)
这个模型的构建和训练分为两个截然不同的阶段:演化搜索阶段和最终训练阶段。
阶段一:演化搜索 (Evolutionary Search)
此阶段的目标是找到最优的架构(即基因型 $[X, M, G]$)。
* 训练方式:无训练 (Training-free)。
* 评估指标:使用 BIE (Brain-inspired Indirect Evaluation)。
* 原理:不进行反向传播更新权重。直接初始化随机权重的网络,输入少量数据,计算网络输出脉冲模式的稳定性(见后文 BIE 详解)。通过进化算法(锦标赛选择、交叉、变异)迭代 80 代,找到 BIE 得分最高的架构。
阶段二:最终训练 (Final Training)
此阶段的目标是训练搜索到的最优架构的权重 $W$。
* 训练方式:监督学习 (Supervised Learning)。
* 算法:时空反向传播 (STBP) 配合 代理梯度 (Surrogate Gradient)。
* 问题:脉冲发放函数 $S[t] = \Theta(V[t] - V_{th})$ 是阶跃函数,导数处处为0或无穷大,导致无法直接使用梯度下降。
* 解决 (代理梯度):在反向传播计算 $\frac{\partial S}{\partial V}$ 时,使用一个平滑的可导函数(如矩形函数或 sigmoid 导数)来近似阶跃函数的导数。
$$
\frac{\partial S}{\partial V} \approx h(V)
$$
文中实验部分提到的训练方法 STBP (Spatio-Temporal Backpropagation) 就是利用这种机制,在时间和空间维度上同时反向传播误差,更新卷积核权重 $W$。
II. 核心贡献与方法 (Method)
A. 多尺度演化编码 (Multi-scale Encoding)
MSE-NAS 将搜索空间分解为微观、介观和宏观三个尺度,编码为基因型 $[X, M, G]$。
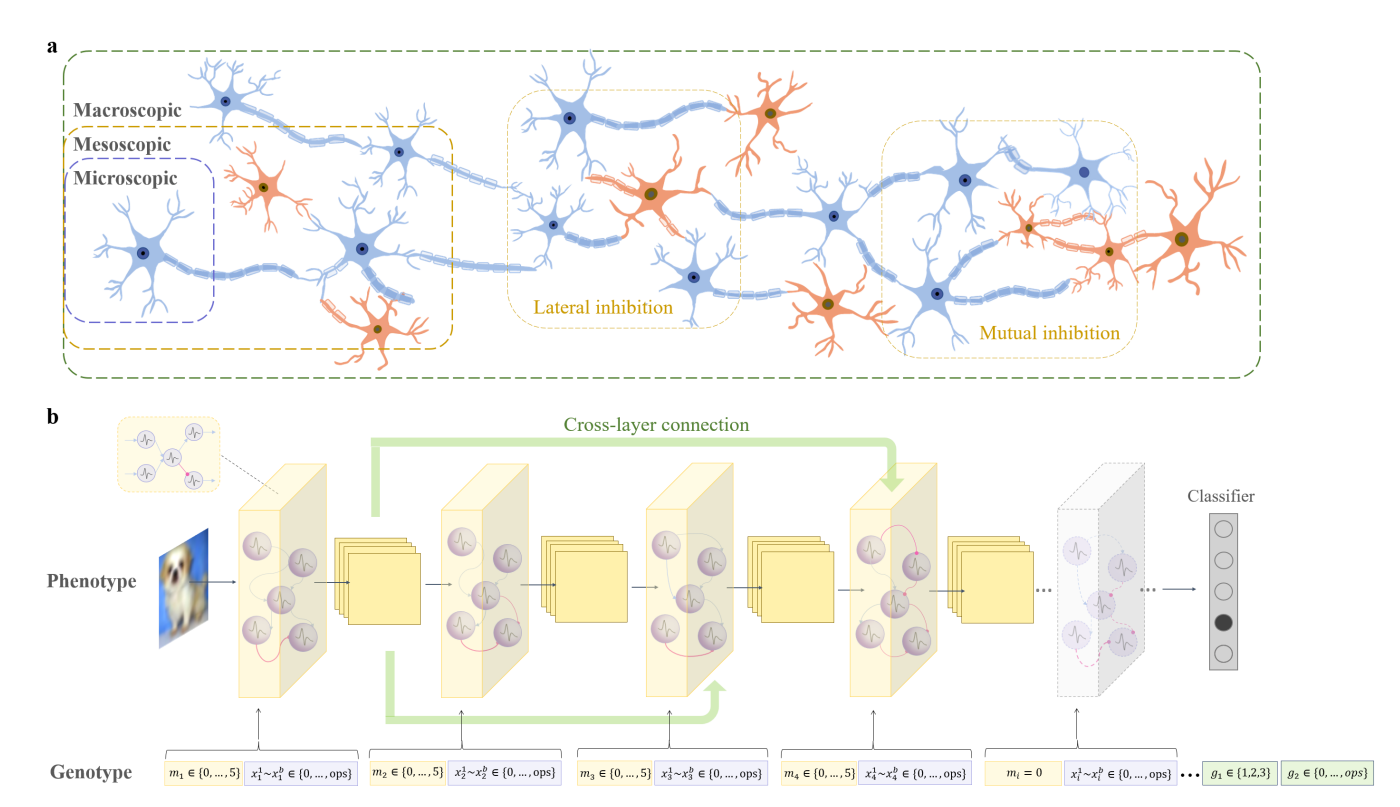
基因型定义:
假设网络最大层数为 $l$,每个层由 $b$ 个基因编码微观操作。基因型表示为:
$$ [X, M, G] = [(m_1, x_1^1, ... x_1^b), ..., (m_l, x_l^1, ... x_l^b), g_1, g_2] \tag{2} $$
各部分数学含义如下(详见 Table I):
-
微观尺度 (Micro, $X$):
- $x_i^k \in \{0, 1, 2\}$:定义模体内部神经元的具体突触操作。
- 取值:0 (Empty), 1 (3x3 Conv), 2 (5x5 Conv)。这意味着每个神经元的输入连接可以是不同感受野的卷积。
-
介观尺度 (Meso, $M$):
- $m_i \in \{0, 1, 2, 3, 4, 5\}$:定义第 $i$ 层的神经微电路类型。
- 对应关系:0 (空层), 1 (FE), 2 (FI), 3 (FbI), 4 (LI), 5 (MI)。
- $m_i$ 决定了层内的兴奋性 (Excitatory) 和抑制性 (Inhibitory) 神经元的连接拓扑结构(如图1所示)。
-
宏观尺度 (Macro, $G$):
- $g_1 \in \{1, 2, 3\}$:定义层间连接模式(跨层连接)。
- $g_2 \in \{1, 2\}$:定义跨层连接的卷积核大小。
B. 脑启发间接评估 (Brain-inspired Indirect Evaluation, BIE)
为了避免在搜索阶段进行昂贵的 STBP 训练,作者提出了 BIE。其核心假设是:一个好的、鲁棒的大脑结构,其神经活动模式在面对不同输入时应保持一定的内在稳定性(Homeostasis),即对输入的微小变化不应产生剧烈的崩塌或爆发。
1. 发放模式 (Firing Pattern)
对于一个个体 $Individual_i$,输入样本后,统计 $n_{neu}$ 个神经元在 $T$ 时间步内的发放总数向量 $P_i$:
$$ P_i = \left(\begin{array}{ccc} \sum_0^T p_1^t & \cdots & \sum_0^T p_{n_{neu}}^t \end{array}\right) \tag{3} $$
其中 $p_z^t \in \{0, 1\}$ 表示神经元 $z$ 在 $t$ 时刻是否发放。
2. 差异矩阵 (Difference Matrix)
输入一批样本(Batch size = $j$),计算同一个体对不同样本响应的差异矩阵 $BIE_i$。差异度量采用曼哈顿距离 $d(u,v)$:
$$ BIE_{i} = \begin{pmatrix} d(P_{i}^{1}, P_{i}^{1}) & \cdots & d(P_{i}^{1}, P_{i}^{j}) \\ \vdots & \ddots & \vdots \\ d(P_{i}^{j}, P_{i}^{1}) & \cdots & d(P_{i}^{j}, P_{i}^{j}) \end{pmatrix} \tag{5} $$
3. 优化目标
演化的目标是最小化同一网络对不同样本响应的差异(即追求架构层面的活动稳定性)。适应度函数定义为:
$$ \underset{[X_{i},M_{i},G_{i}]}{\arg\min} \frac{1}{s} \sum_{j=1}^{s} BIE_{i}^{j} \tag{7} $$
这相当于在寻找一种架构,使得未经训练的随机权重网络就能表现出对输入数据的某种“一致性”或“稳定性”,这被视为良好可塑性的先验。
III. 实验与分析 (Experiments)
A. 性能表现 (Results)
MSE-NAS 在多个数据集上均取得了 SOTA 效果,优于人工设计的 SNN 和其他 NAS 方法。
| 数据集 | 方法 | 准确率 (Accuracy) | 优势 |
|---|---|---|---|
| CIFAR10 | MSE-NAS (STBP) | 96.58% | 比 ResNet-19 (TET) 高 2.14%,比 AutoSNN 高 3.43% |
| CIFAR100 | MSE-NAS (STBP) | 80.56% | 比其他 NAS 方法高 7%~11% |
| CIFAR10-DVS | MSE-NAS | 84.0% | 显著优于 VGGSNN (TET) |
| DVS128-Gesture | MSE-NAS | 98.10% | SOTA |
B. 消融实验与发现
- E/I 平衡 (Excitatory/Inhibitory Balance):实验发现,性能最好的个体倾向于拥有兴奋-抑制平衡的模体组合。这与生物脑中维持 E/I 平衡以实现临界态(Criticality)的机制一致。
- 宏观连接:跨层连接显著提升了性能,证明了类似 ResNet 的跳跃连接在 SNN 中同样重要。
C. BIE 的效率
在 CIFAR10 上,BIE 评估仅需 0.83 GPU Hours,而传统的 Train-then-Evaluate 方法需要 50 GPU Hours,速度提升了 60倍。
IV. 结论 (Conclusion)
本文提出的 MSE-NAS 成功将生物脑的多尺度拓扑演化机制引入 SNN 架构搜索。
1. 结构融合:通过卷积(突触)与 LIF(神经元)的结合,利用微观、介观、宏观的多尺度编码,构建了类脑的深层 SNN。
2. 两阶段优化:利用 BIE 进行快速的无训练进化搜索,再通过 STBP 代理梯度进行有监督的权重训练。
3. 生物解释性:演化结果自发涌现出 E/I 平衡特性,验证了类脑结构的优越性。